特征值分解 主成分分析

机器学习 数理统计

---

前言

       线性代数在机器学习中应用的十分广泛，如果想对机器学习有比较深入的了解的话，我认为必要的数学基础还是需要的，本篇文章就来简单介绍一下应用广泛的特征值和特征向量，顺便为我之后那篇《马氏距离》做一个铺垫。

矩阵乘法

       首先，先简单说一下矩阵乘法的几何意义。矩阵乘法实际上就是对应着一个变换，将一个向量进行旋转伸缩的变换。如果这个矩阵对于某些向量只发生伸缩变换，那么我们就可以将这些向量称为这个矩阵的特征向量，伸缩比例就是特征值。
       假设有矩阵 $M$ 如下，那么它对应的线性变换就如同下图所示：

$$M = \begin{bmatrix} 3 & 0 \\ 0 & 1 \\ \end{bmatrix}$$

       这是由于矩阵 $M$ 是一个对称矩阵，所以这个变换是一个对 $x$ 轴、 $y$ 轴方向的拉伸变换，如果 $M$ 不是对称矩阵，如下，那么这个矩阵所描述的变换就发生的了改变：
$$M = \begin{bmatrix} 1 & 1 \\ 0 & 1 \\ \end{bmatrix}$$

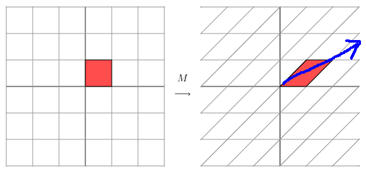
特征值与特征向量

       如果我们说一个向量 $v$ 是方阵 $A$ 的特征向量，将一定可以表示成下面的形式：

$$Av = \lambda v$$
       其中 $\lambda$ 为一标量，称为 $v$ 对应的特征值，同样 $v$ 也称为 $\lambda$ 的特征向量（换言之，特征向量 $v$ 被施以线性变化 $A$ ，只会使向量 $v$ 发生伸缩）。
       由上式可知：
$$p(\lambda) = det(A - \lambda I) = 0$$
       我们可以对上述多项式进行简单的因式分解得到：
$$p(\lambda) = (\lambda - \lambda_1)^{n_1}(\lambda - \lambda_2)^{n_2}...(\lambda - \lambda_k)^{n_k}$$
       其中：
$$\sum_{i=1}^{k} = N$$
       对于每一个特征值 $\lambda_i$，我们都有下式成立：
$$(A - \lambda_iI)v = 0$$
       对于每一个特征方程，都会有 $m_i(1 \le m_i \le n_i$个线性无关的解。这$m_i$个向量与特征值 $\lambda_i$ 相对应。这里整数 $m_i$ 成为特征值 $\lambda_i$ 的几何重数。

矩阵的特征分解

       令 $A$ 是一个 $N \times N$ 的方阵，且有 $N$ 个线性无关的特征向量 $q_i(i = 1,...,n)$ 。那么， $A$ 可以被分解成：

$$A = Q\Lambda Q^{-1}$$
其中，$Q$是一个 $N \times N$ 的方阵，且其第$i$列为$A$的 特征向量$q_i$。$\Lambda$为对角矩阵，其对角线的元素为对应的特征值，即$\Lambda_{ii}=\lambda_i$（只有可对角化的矩阵才可以作特征分解）。
       一般来说，特征向量$q_i(i = 1,2,...,N)$一般被正交单位化（但这不是必须的）。未被正交单位化的特征向量组$v_i(i = 1,2,...,N)$也可以作为$Q$的列向量。

通过特征分解求矩阵的逆矩阵

       若矩阵$A$可被特征分解并特征值中不含零，则矩阵$A$为非奇异矩阵，且其逆矩阵可以由下式给出：

$$A^{(-1)} = Q\Lambda^{-1} Q^{-1}$$
       又因为$\Lambda$是对角矩阵，所以其逆矩阵很容易算得出来：
$$[\Lambda^{-1}]_{ii} = \frac{1}{\lambda_i}$$

对称矩阵

       任意的 $N \times N$ 实对称矩阵都有 $N$ 个线性无关的特征向量。并且这些特征向量都可以正交单位化而得到一组正交且模为 $1$ 的向量。故实对称矩阵$A$可被分解成：

$$A = Q\Lambda Q^T$$
       其中$Q$为正交矩阵，$\Lambda$为实对角矩阵。

PCA主成分分析

       对于空间中的离散点，我们希望降维以后尽可能分散，而这种分散程度在数学是可以采用方程来衡量。假设我们已经把字段的均值全部转化为0了，那么方差可以表示为：

$$Var(a) = \frac{1}{m}\sum_{i = 1}^ma_i^2$$
       也就是意味着：我们希望找到一组基，使得所有数据变化为这个基上的坐标表示后，方程值最大。
       但是，如果只使用这种方式进行分析的话，在寻找第二个基时，这两个应该是几乎完全重合的，很显然这样的维度是没有用的。直观的说，让两个字段能够表示更多的原始信息，我们不希望它们之间存在着（线性）相关，也就是协方差为0。那么，在均值为0的条件下，协方差为：
$$Cov(a, b) = \frac{1}{m}\sum_{i = 1}^{m}a_ib_i$$
       那么，我们的目标为：将一组N维向量降为K），其目标是选择K个单位（模为1）正交基，使得原始数据变换到这组基上后，各字段两两间协方差为0，而字段的方差则尽可能大。
       设相应的协方差矩阵为$C = \frac{1}{m}XX^T$，$Y$是相应的低维向量，而$P$是对应的两者之间的转换$Y = PX$，$D$为$Y$的协方差：
$$D = \frac{1}{m}YY^T \\ =\frac{1}{m}PXX^TP^T \\ =P(\frac{1}{m}XX^T)P^T =PCP^T$$
       因此，我们的优化目标变成了寻找一个矩阵$P$，满足$PCP^T$是一个对角矩阵，并且对角元素按从大到小依次排列，那么$P$的前K行就是要寻找的基，用$P$的前K行组成的矩阵乘以X就使得X从N维降到了K维并满足上述优化条件。
       至此就可以通过很简单的特征值分解完成整个过程了。

奇异值分解

       下面简单聊一下奇异值分解，特征值是一个提取矩阵特征很不错的方法，但是这只是对方阵而言，应用面略微有点窄。奇异值分解则是一个能适用于任意一个矩阵的一种分解方法：

$$M = U \Sigma V^T, \,$$
       其中，$M$是一个$m \times N$的矩阵，$U$是一个$m \times m$的正交矩阵，又称为左奇异向量，$\Sigma$则是$m \times n$的对角矩阵，同样$V^T$也是一个正交矩阵，又称左奇异向量。其中，$\Sigma$对角上的元素$\Sigma_{ii}$即奇异值。
       那么，奇异值如何与也特征值联系到一起呢？我们给定上述的$M$的奇异值分解，那么：
$$M^TM = V\Sigma^TU^TU\Sigma V^T \\ = V\Sigma^TI\Sigma V^T \\ = V(\Sigma^T\Sigma)V^T \\ $$
       很显然，我们完成了方阵$M^TM$的特征值分解。同样$(\Sigma^T\Sigma)$对角便是特征值，一般来说，奇异值$\sigma_i = \sqrt{\lambda_i}$，同样我们有下式：
$$M^TMv_i = \lambda_iv_i$$

总结

       PCA本质上是将方差最大的方向作为主要特征，同时让它们在不同正交方向上没有相关性。
       同样，PCA也存在一些限制，它解除线性相关，但是对于高阶相关性就没有办法（对于存在高阶相关性的数据，可以考虑Kernel PCA，通过Kernel函数将非线性相关转为线性相关）。另外，PCA假设数据各主特征是分布在正交方向上，如果在非正交方向上存在几个方差较大的方向，PCA的效果就不会十分理想。
       最后需要说明的是，PCA是一种无参数技术，也就是说面对同样的数据，结果都一样，所以PCA便于通用实现，但是无法实现一些个性化的需求。

参考

特征分解
PCA的数学原理