局部加权线性回归

机器学习 CS229

---

       本文主要参考自加权最小二乘法与局部加权线性回归 ，对其中的内容进行了一致性的修改并且填补了没有说明的数学知识。

概述

       在之前的线性回归中，我们采用了不止一种方法（以后遇到有意思的方法还会加到其中），其中有一种方法是最小二乘回归，在统计学上，那篇文章中的最小二乘法回归称为普通最小二乘法（OLS），这是一种有约束条件的线性回归，本篇文章我们将通过介绍局部加权线性回归来讲这些内容都一并讲述一遍。

普通最小二乘法

       如同前面的文章一样，我们定义 $e$ 为随机误差，那么我们可以得到：

$$y = h(X) + e \\ = X\theta + e$$
       普通最小二乘法实际上就是使得残差平方和达到最小，即：
$$RSS = ||y - X\theta||^2 = (y - X\theta)^T(y - X\theta)$$
       很容易我们可以得到 $\theta$ 的估计值为 $(X^TX)^{-1}X^Ty$ ，那么在Gauss-Markov假设条件下，我们可以认为普通最小二乘法所求的线性回归就是最佳无偏估计。而Gauss-Markov假设条件则是以下三条：
$$E(e) = 0 \\ Var(e) = \sigma^2I \\ Cov(X,e) = 0 \\ $$
       上式中， $Cov()$ 表示的是协方差，三条公式的表达的意思分别是：

1. 在给定 $X$ 的条件下， $e$ 的条件期望为零，即：
   $$E(e_i|X_i) = 0$$
2. 在给定 $X$ 的条件下， $e$ 的条件方差为一个常数 $\sigma^2$ ，即：
   $$Var(e_i|X_i) = \sigma^2$$
3. 特征 $X_i$ 是非随机的，或者虽然 $X_i$ 是随机但与 $e_i$ 不相关，即：
   $$Cov(X_i,e_i) = 0$$

       其实这里还有一些事情我们并没有注意到，在计算残差平方和的时候在本质上我们采用的并不是欧氏距离之差，而是马氏距离之差，只不过是因为欧氏距离是马氏距离的特殊情况（关于马氏距离的内容参见后续文章），所以才在 $RSS$ 的推导公式中表现为欧氏距离，实际上 $RSS$ 的推导公式应该如下：

$$RSS = (y - X\theta)^TI^{-1}(y - X\theta)$$
       由于 $I$ 是单位矩阵，所以公式就可以化简为前述形式。再说一些没有的，但是比较有意思的东西。
       我们将 $RSS$ 的公式化简，那么会有：
$$RSS = (y - X\theta)^T(y - X\theta) \\ = y^Ty - y^TX(X^TX)^{-1}X^Ty \\ = y^T[I - X(X^TX)^{-1}X^T]y \\ = y^T[I - H]y$$
       其中， $H = X(X^TX)^{-1}X^T$ ，这个矩阵 $H$ 称为投影矩阵（关于投影矩阵请参见后续文章）。对于普通最小二乘法的内容基本就到这里了，这部分还有不少东西没有完全搞懂，等我有时间刷一下线代再来重修改下。

广义最小二乘法

       如果不能够满足高斯-马尔科夫假设，那么我们上述所有的推导很研究都是存在问题的。我们适当放宽假设条件，考虑这样一个模型：

$$E(e) = 0 \\ Var(e) = \sigma^2\Sigma \\ Cov(X,e) = 0 \\ $$
       三个假设只是将其中的单位矩阵替换为一个已知的正定对称矩阵$\Sigma$，这就是意味着 $Cov(e_i,e_j) \neq 0$ ，也就是不要求误差项之间保证不相关了。那么我们的残差平方和会变为：
$$RSS = (y - X\theta)^T\Sigma^{-1}(y - X\theta)$$
       在这种情况下，我们的权重向量 $\theta$ 的推导公式也发生了相应的改变：
$$\theta = (X^T\Sigma^{-1}X)^{−1}X^T\Sigma^{-1}y$$

加权最小二乘法

       加权最小二乘法则是广义最小二乘法的特殊情况，广义最小二乘法中的 $\Sigma$ 太自由了，我们对其增加一些限制，我们认为它取对角矩阵，这个对角矩阵的对角元都是权重 $\omega$ 的倒数，如下：

$$Cov(e) =\begin{bmatrix} \frac{1}{\omega_1} & 0 & \cdots\ & 0 & 0 \\ 0 & \frac{1}{\omega_2} & \cdots\ & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 0 & \frac{1}{\omega_n} \\ \end{bmatrix}$$
       很显然， $\omega_i$ 表示的就是第$i$个样本在回归中的权重，具有较小方差的样本给予较大的权重，在回归问题中更加重视。我们用$W$表示权重矩阵，那么 $\Sigma^{-1} = W$ ，那么：
$$RSS = (y - X\theta)^TW(y - X\theta) \\ \theta = (X^TWX)^{−1}X^TWy$$
       我们可以通过一定的转换将上述模型转化成满足普通最小二乘假设的模型。在这里我们 $\Sigma^{-1}$ 的平方根，我们可以很容易的得到这个矩阵：
$$Cov(e) =\begin{bmatrix} \sqrt{\omega_1} & 0 & \cdots\ & 0 & 0 \\ 0 & \sqrt{\omega_2} & \cdots\ & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 0 & \sqrt{\omega_n} \\ \end{bmatrix}$$
       我们在回归矩阵两端都乘以矩阵 $C$ ，得到：
$$Cy = Ch(X) + Ce \\ = CX\theta + Ce$$
       此时，我们需要的事情发生了，这时 $Ce$ 的协方差矩阵为：
$$Var(Ce) = CVar(e)C^T \\ = \sigma^2 C\Sigma C^T = \sigma^2 I$$
       其中第一个等号是根据公式 $Var(AX) = AVar(X)A^T$ 推导的，证明过程参见Var（AX）=AVar（X）A如何推导的。到现在我们就得到了满足高斯马尔科夫假设的普通线性回归模型了。采用此模型推导出来的 $\theta$ 值与原模型是完全相同的，而且我们可以认为普通最小二乘法所求的线性回归就是最佳无偏估计。

局部加权线性回归

       终于到我们的正题了，局部加权线性回归是一种经典的机器学习算法，在一定程度上解决了普通的线性回归方程所存在的欠拟合和过拟合的现象。与普通线性回归不同，普通线性回归是一种参数方法，在计算出 $\theta$ 后，只要将新的数据带入即可进行预测，我们并不需要保留数据集。然而局部加权线性回归则是一种非参数方法，每次计算都需要重新学习一个参数 $\theta$ ，所以需要保留数据集。那么它是怎么运作的呢？
       实际上，局部加权线性回归其实就是把每个点根据与待测的距离，赋予一定的权重，也就是增加一个核函数矩阵 $W$ 。那么我们需要最小化的目标函数大概为：

$$\sum_{i}w(y^{(i)}-\hat y^{(i)})^2$$
       而权重（ $\theta$ ）的估计项：
$$\theta = (X^TWX)^{−1}X^TWy$$
       很显然，这就是加权最小二乘法，我们前面讨论的东西终于用到了。Andrew Ng在Coursera中使用了高斯核函数，形式如下：
$$w_i = exp\left( - \frac{(x^{(i) -x})^2}{2\tau^2} \right)$$
       需要注意的是，上式只是在形式上与高斯分布相似，但并不具有直接的联系，权重并不是一个随机变量。 $\tau$ 被称为带宽，它控制着数据权重的下降速度。 $\tau$ 越小，权重下降速度越快。

例子

       为了方便起见我们就采用比较简单的一元线性回归，其中 $y = x + \sin{0.3 * i}$ ，同时我们认为偏差服从高斯分布，那么我们可以根据以下代码生成一个简单的实例：

from math import *
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats
mpl.style.use('ggplot')
plt.figure(figsize=(12, 6))
# x取值1~100 y表示非线性函数
x = np.arange(1, 101)
x = np.array([floor(i) for i in x])
y = x + [10 * sin(0.3 * i) for i in x] + stats.norm.rvs(size=100, loc=0, scale=1.5)
plt.scatter(x, y)
plt.show()

       为了让大家能有一个对这个函数能有一个更清楚的认识，我们将图像绘制如下：

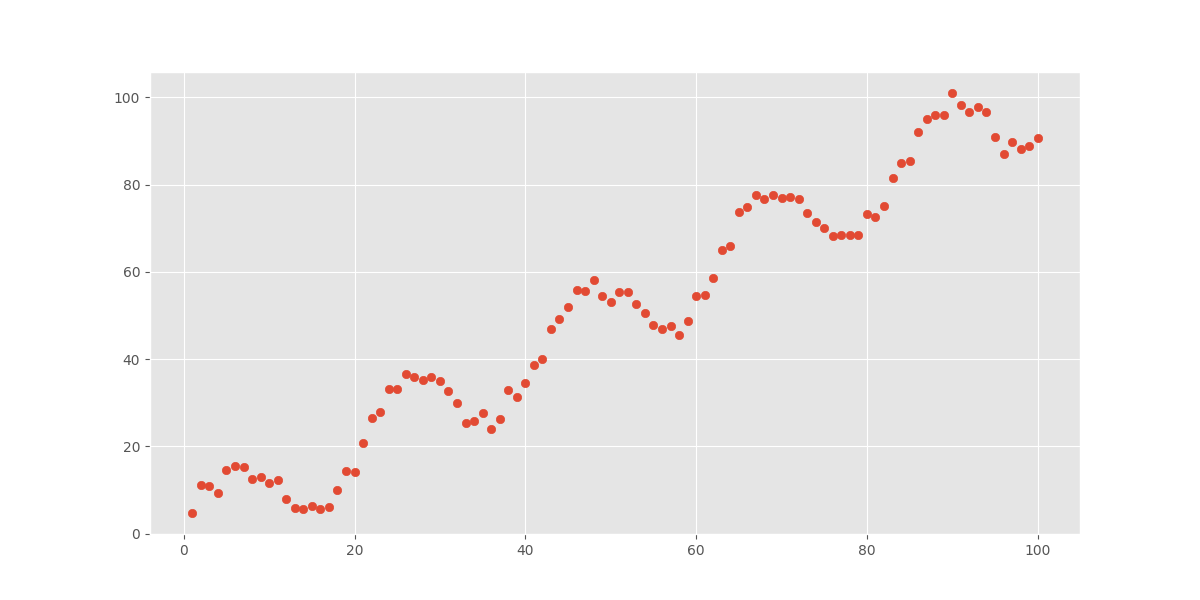
       其实很明显，这是一个非线性关系（研究 是否是广义线性关系？）的样本数据，我们先采用普通最小二乘法来拟合这一问题：

# 调用scipy.stats中自带的线性回归函数
slope, intercept, r_value, p_value, std_err = stats.linregress(x, y)
yHatLinear = intercept + slope * x
plt.plot(x, yHatLinear, 'r', color='blue')

       我们可以预想到效果并不会很理想，事实也确实如此：

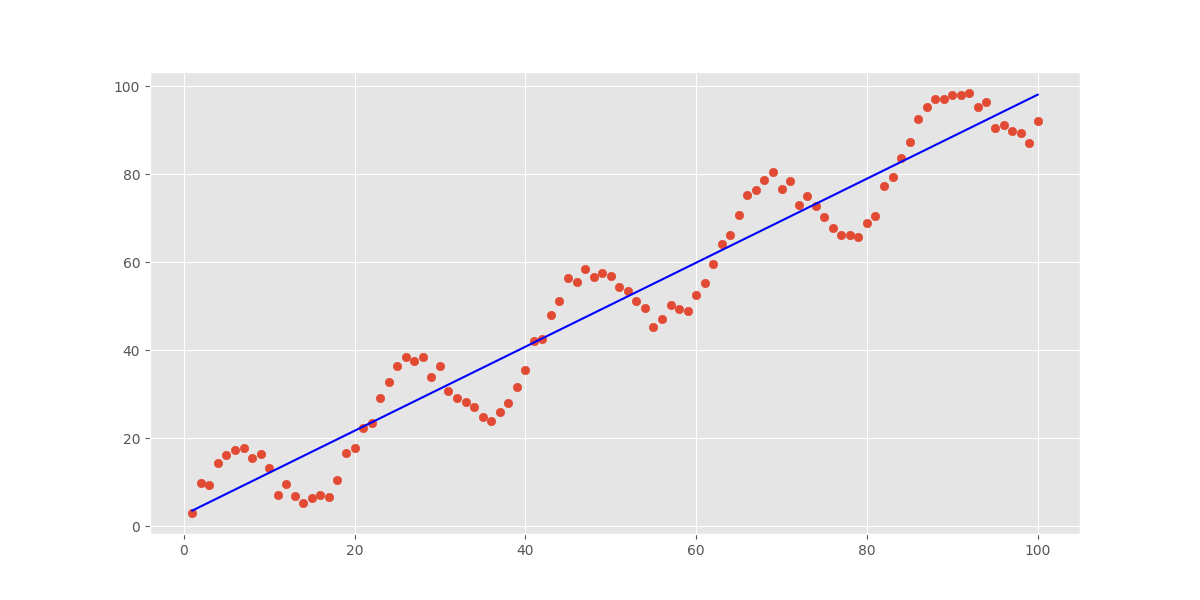
       而对于局部加权线性回归则不会出现这种现象，只要我们合理调节$\tau$就可以得到较好的拟合（这一部分代码利用了加权最小二乘法向普通最小二乘法转换的小技巧，同时numpy、statsmodels这两个包我还不是特别熟练，所以只是理解了代码并未进行改写）：

def get_sqrtW(x0, k):
    w = np.zeros(len(x))
    for i in range(len(x)):
        w[i] = exp(-(x[i] - x0) ** 2 / (2 * k * k))
    w = np.array([sqrt(i) for i in w])
    return w
def get_yHat2(k):
    yHat2 = np.zeros(len(x))
    for i in range(len(x)):
        w = get_sqrtW(x[i], k)
        x2 = w * x
        x2 = x2[x2 > 0]
        y2 = w * y
        y2 = y2[y2 > 0]
        X = np.zeros((1, len(x2)))
        X[0] = x2
        X = X.T
        X = sm.add_constant(X, has_constant='skip')
        X[:, 0] = w[w > 0]
        Y = y2
        model = sm.OLS(Y, X)
        results = model.fit()
        a = results.params[0]
        b = results.params[1]
        yHat2[i] = a + b * x[i]
    return yHat2
yHat2 = get_yHat2(100000)  # ｋ取100000
plt.figure(figsize=(12, 6))
plt.plot(x, yHat2, 'r')
plt.scatter(x, y)
plt.show()

       当 $\tau$ 分别为10000、10、1以及0.1时，拟合效果如下四图所示：




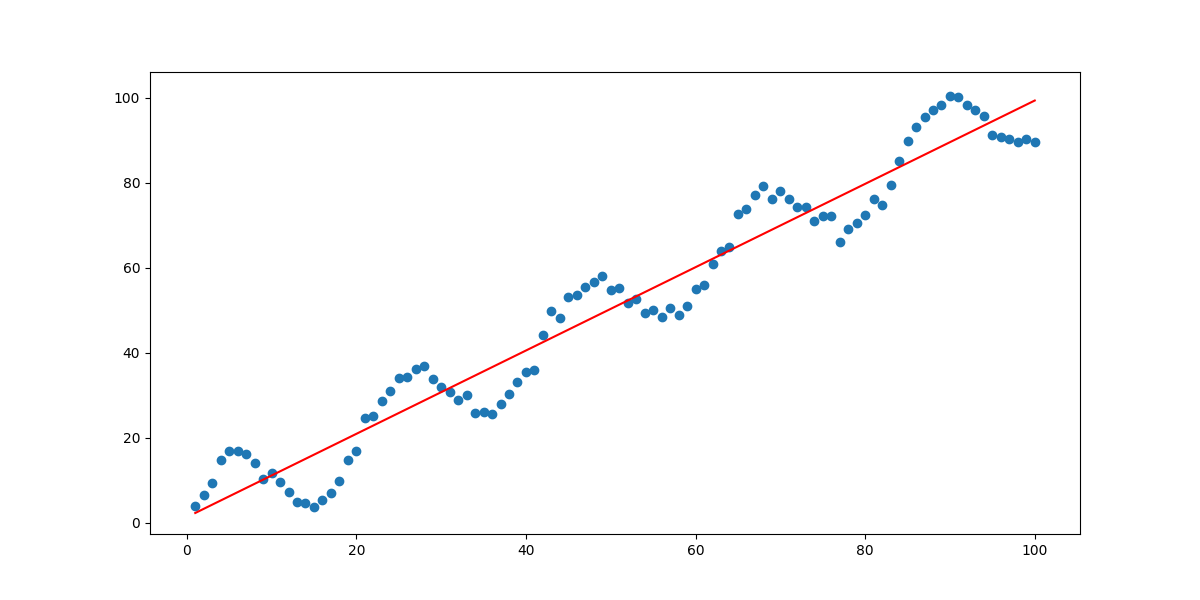
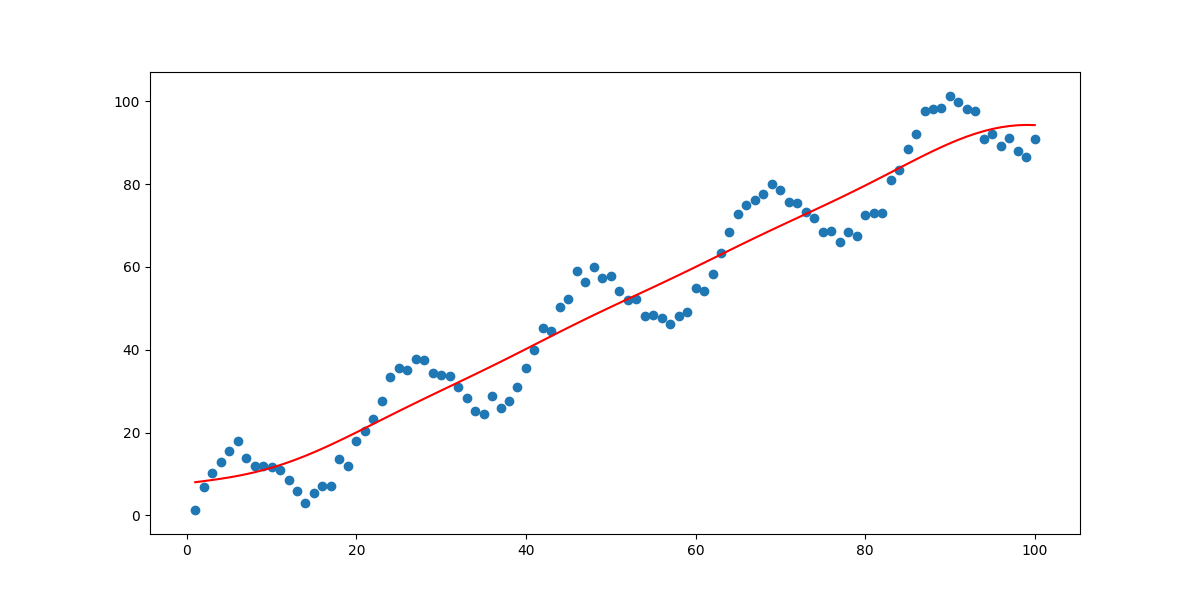
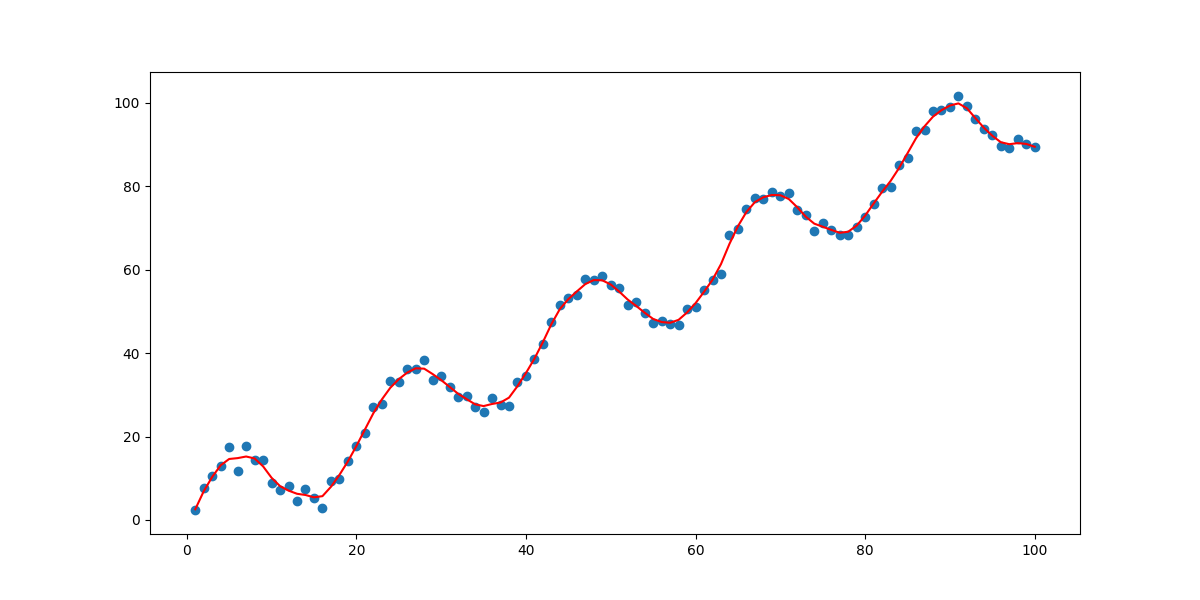
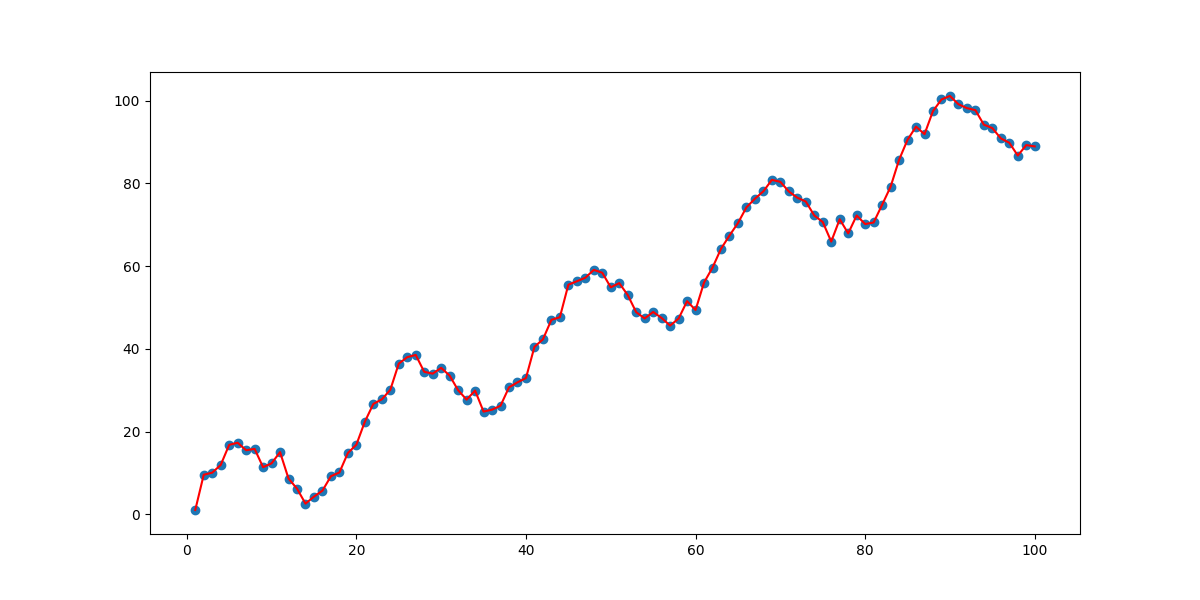
       效果跟我们之前预料的完全相同，在 $\tau$ 取值过小时，会发生过拟合现象，过大则会出现欠拟合。所以 $\tau$ 的取值对我们的回归效果起到了决定性的作用。

结语

       这篇文章真的远远比我想象的费时间，因为前文中提到了博客将我的整个计划都打乱了，看了好多额外的内容，反复修改了三四次，尤其是在广义线性回归那部分真的研究了好久，最后还是通过阅读Wiki的内容基本完成了对这一部分的理解。总的来看，这篇文章不是很满意，等有时间一定要好好梳理下。

参考

Ordinary least squares
Residual sum of squares
加权最小二乘法与局部加权线性回归

---