@ShixingWang
2016-06-21T13:00:10.000000Z
字数 6265
阅读 2847
| 姓名 | 学号 | 班级 | 选题 | 论述 | 结论 | 分数 |
|---|---|---|---|---|---|---|
| 王世兴 | 2013301020050 | 13级弘毅班 |
物理与计算在蛋白质折叠模型中的应用
王世兴 2013级弘毅班 2013301020050
摘要
蛋白质是生物体营养物质之一,也是生命活动的主要承担者。本文在二维正方形格子中,利用一个简化的“玩具模型”对多肽链进行描述,考虑分子间作用力,利用正则系综计算了体系的能量,并用蒙特卡罗算法模拟多肽链卷曲折叠形成蛋白质的过程。给出了不同蒙特卡洛模拟步长下一个短链氨基酸的位形,另外计算了特定温度下同一短链氨基酸的能量和多肽链端点间距离随模拟时间的变化。讨论了计算结果与参考文献差距的可能原因。
关键词: 蛋白质 分子间作用力 蒙特-卡罗模拟
Abstract
The protein serves as one of the nutrition materials and undertakes most biological functions. A simplified ``toy model'' is used in a two-dimensional plain to describe the polypeptide chain. The canonical ensemble is used to calculate the energy of the system, concerning the intermolecular forces. The folding and rolling of the polypeptide chain into a protein is simulated with Monte-Carlo algorithm. Various configurations of a short chain of polypeptide is given after various Monte-Carlo time lengths. The energy and end-to-end length are calculated as a function of simulation time. Also the deviation of the results from those from references is discussed.
Key workds: Protein inter-molecular interaction Monte-Carlo simulation
引言
理论预言蛋白质结构的理论基础
几乎在DNA双螺旋结构确定的第一时间,DNA结构的提出者之一弗朗西斯·克里克就提出了“中心法则”[1][2],概括了遗传信息在生物体内的流动方式。DNA 在DNA解旋酶、DNA 聚合酶的作用下通过复制在母代和子代之间传递,同时通过DNA解旋酶、RNA聚合酶的作用将遗传信息从DNA转录到mRNA中,再由RNA在核糖体、tRNA 的协助下经过翻译将游离的氨基酸组装成多肽链,多肽链折叠形成复杂结构,成为能承担生物功能的蛋白质。克里克的文章中强调了遗传信息的单向流动性[2],而在之后的研究中,人们陆续发现了RNA 的复制、RNA逆转录现象,这些也都成为了现代中心法则的一部分。肽病毒是现在已知的唯一例外。
蛋白质是以氨基酸为单体,通过缩合反应形成的生物大分子。从病毒到真核细胞,蛋白质中使用到的氨基酸相同且仅有20种。组成蛋白质的氨基酸机构上具有相似性,均为α-氨基酸,即同一个碳原子的四个共价键分别为一个氨基、一个羧基、一个氢原子和一个侧链基团(也可以是氢原子)。在核糖体中,两个相邻氨基酸分别脱去氨基中的一个氢原子和羧基中的一个羟基,形成一个肽键和一个游离水分子,这一反应被称为脱水缩合反应。[3] 部分氨基酸的侧脸集团中含有硫原子等电负性较高的原子,基团的极性使得当肽链卷曲至某种位形时原本不相邻的氨基酸可以通过二硫键、氢键,范德瓦尔斯力等分子间相互作用力形成α-螺旋,β-折叠等二级结构和三级结构,三级结构的多个多肽进一步形成四级结构,此四级结构构成能够完成生物功能的蛋白质。
生命体是一个开放系统,绿色植物通过太阳供给的能量,将无序的无机物(大气中的二氧化碳和土壤中的水等)转化为有序的营养物质,实现局部的熵的减小[4]。但若只研究多肽链形成二级结构的过程, 20 世纪60年代,Anfinsen基于还原变性的牛胰岛RNase蛋白在不需其他任何物质帮助下,仅通过去除变性剂和还原剂就使其恢复天然结构的实验结果,提出了“多肽链的氨基酸序列包含了形成其热力学上稳定的天然构象所必需的全部信息”的“自组装学说”[5]。 Anfinsen的“自组装热力学假说”得到了许多体外实验的证明,尤其是一些小分子量的蛋白。但是另一方面,体内蛋白质的折叠往往需要有其他辅助因子的参与,并伴随有ATP的水解供能,这表明蛋白质的折叠不仅仅是一个热力学的过程,显然也受到动力学的控制,而且能量输入暗示了部分蛋白质的组装过程可能也是远离平衡态的熵减过程。本文作为一个简单的讨论,考虑结构简单的多肽链,仍采用“自组装热力学假说”作为前提,即认为给定一个多肽链的氨基酸序列,经过时间演化,其能量最低态就是在生物体中发挥功能的蛋白质构型。
蛋白质折叠的“玩具模型”及其正则系综描述
三维结构的蛋白质折叠情况复杂,对计算机的计算效率的要求较高。为此,我们将问题简化为二维方形格子中的玩具模型。如图(1)所示,方形格子的顶点代表氨基酸可能占据的位置,黑色实线段代表某一时刻的蛋白质构型,圆点代表蛋白质的单体氨基酸,黑色实线段代表相邻氨基酸之间的肽键。在这样的模型中,不允许两个氨基酸占据同一个格点,从而多肽链不能交叉。由于分子间作用力较弱,仅当两个在序列上不相邻的氨基酸占据相邻两个格点时才会计算其分子间相互作用。两个氨基酸之间的相互作用由氨基酸的种类决定。由于组成蛋白质的共有20中氨基酸,所以这一能量由一个20×20的对称矩阵J描述。在图(1)中,仅考虑图中画出的氨基酸,则变换前后两种结构的能量相等。但若在10位点下方一个位点也有氨基酸的话,则新位形的能量更低。
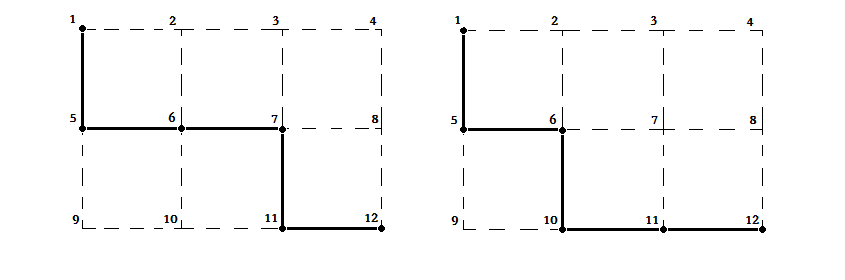
Figure final.1 氨基酸空间位置改变的示意图。左图:某一次位形改变之前的多肽链构型;右图:7位点处的氨基酸移动到10之后的位形
统计物理[6]中,平衡态下一个仅与温度为T的热库进行能量传递而无物质交换的系统可用正则系综描述,系统处在状态r的概率为
其中T为热库的温度。
在本问题中,由于肽键是共价键,其键能远大于分子间作用力的能量,在蛋白质折叠问题中视作完全不可断裂,从而我们可以讲系统能量的零点设为肽链仅以肽键相连的状态。那么整个体系的能量
其中表示肽链的第m和第n个氨基酸,求和对所有m,n的组合进行,A(i)表示第i个氨基酸的种类。当第m和第n个氨基酸处在最近邻位置且两者之间并非共价键连接时
玻尔兹曼分布的蒙特卡罗模拟
根据()式对正则系综的描述,对于能量不同的两个状态,在平衡状态下,不同能态之间的概率不随时间变化,也就意味着从某一能态向其他能态跃迁的概率等于从其他能态跃迁到此能态的概率。
从而有
可见多肽链随能量满足玻尔兹曼分布。从高能态到低能态的过程一定能够发生,。低能态跃迁到高能态的概率为,类似于“伊辛模型”的蒙特卡罗模拟方法,利用随机数发生器产生一个伪随机数,当其小于时即允许这一过程发生,反之则保持之前的状态,这样即可保证体系满足玻尔兹曼分布[7]。
方法
J矩阵的具体形式
从量子力学第一性原理计算不同分子间作用力的势场大小的计算难度较大,而一个简化的模型不仅有助于我们把握这一过程的物理图像,而且能带来丰富的结论。氨基酸的侧侧链基团可以初步分为极性和非极性两种,两种基团之间一般来说相互排斥,使得体系能量高于基准能量,阻碍蛋白质折叠。但是对于我们研究的短链蛋白质,在其中考虑这种效应会使得蛋白质很难折叠,难以观察到现象。所以我们选择将所有氨基酸之间的组合的相互作用能设为负值。考虑到温度会使得多肽链存在向高能态激发的概率,我们将相互作用能的取值范围设为到。考虑到不同种类的氨基酸之间的相互作用能不同,我们将J矩阵的元素设为到之间均匀分布的随机数。
蒙特卡罗模拟的流程
我们选择多肽链呈一条直线作为系统的初始状态。设多肽链的长度为N,产生一个从1到N之间的伪随机数以确定被选中的氨基酸,设其坐标为。因为我们选定的是正方形格子,所以要保证临近的氨基酸之间的共价键不断裂或拉伸,这一氨基酸只有最多四个位点可以移动,用随机数选取这四个方向中的任意一个,判断这一点是否已经被多肽链上的其他氨基酸占据,如果没有,则可以用蒙特卡洛方法判断构型改变能否发生。根据()式,分别计算出构型改变之前和之后的能量,作差得,如果,则氨基酸移动到新的位置;如果,则产生一个0-1之间的随机数,若这一段随机数小于,则氨基酸移动到新的位置,反之则保留原有构型。
结果与讨论
不同模拟步长下的多肽链形态
我们通过之前算法进行了模拟,得到了不同蒙特卡罗时间之后的多肽链构象。由于随机选取的氨基酸周围可能没有能够移动的方向,或者选取的移动方向上有其他氨基酸占据,以及新的构象可能比原有构象能量更高,这些都使得大量的模拟步骤中多肽链并不能演化到哪一步的候选构象。可以看出,直到第25 步模拟时,仍只有一个氨基酸的位置发生了改变;而到1000 步时,多肽链仍基本保持一个直链状态,仅在首尾两端有数个氨基酸位置改变,向内翻折使得多肽链两端点之间长度减小。
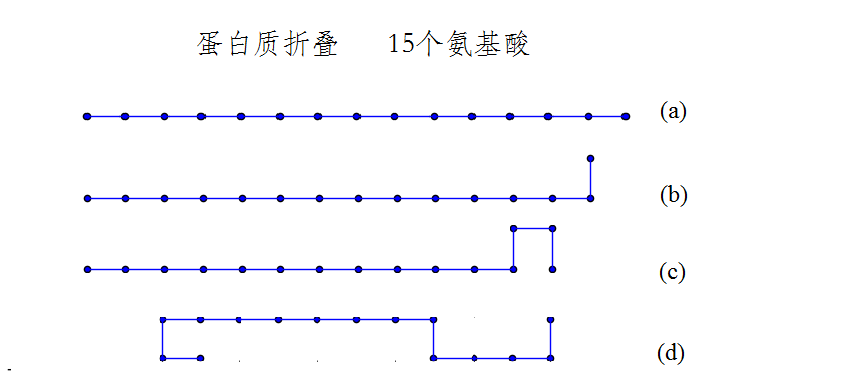
Figure final.2 蒙特卡罗模拟的不同阶段下多肽链的构象。模型刻画了15 个氨基酸构成的多肽链在温度T=10下的四种构型。图中给出了初始态(a),25步模拟之后的构型(b),(c)为250步,(d)为1000步
温度时的蛋白质能量和端点间距离
自然地,我们将()给出的多肽链的能量作为描述系统的一个重要物理量,同时,我们将多肽链首尾两端的氨基酸之间的距离可以用来衡量蛋白质折叠程度。很明显对出初始条件,仅在多肽链的两端的氨基酸能够改变位置,而当分子间作用势能为负时,已经两两结合形成分子间作用力的氨基酸倾向于保持这样的机构,使得 逐渐减小;而由于本模型中共价键为一刚性链,难以破坏且无法交叉(见引言部分),当温度较低时,当多肽链演化到一个能量较低的构象时,()式决定了蛋白质向能量更高的状态激发的概率很小, 减小到一定值时会稳定下来,成为该温度下稳定的结构。随着温度升高,蛋白质达到稳定结构的时间会变长。而温度较高时,多肽链有较高概率被激发到高能态,从而在不同的亚稳态构型之间转换,难以稳定在某一特定构型。这与蛋白质高温下失活的实验现象一致。
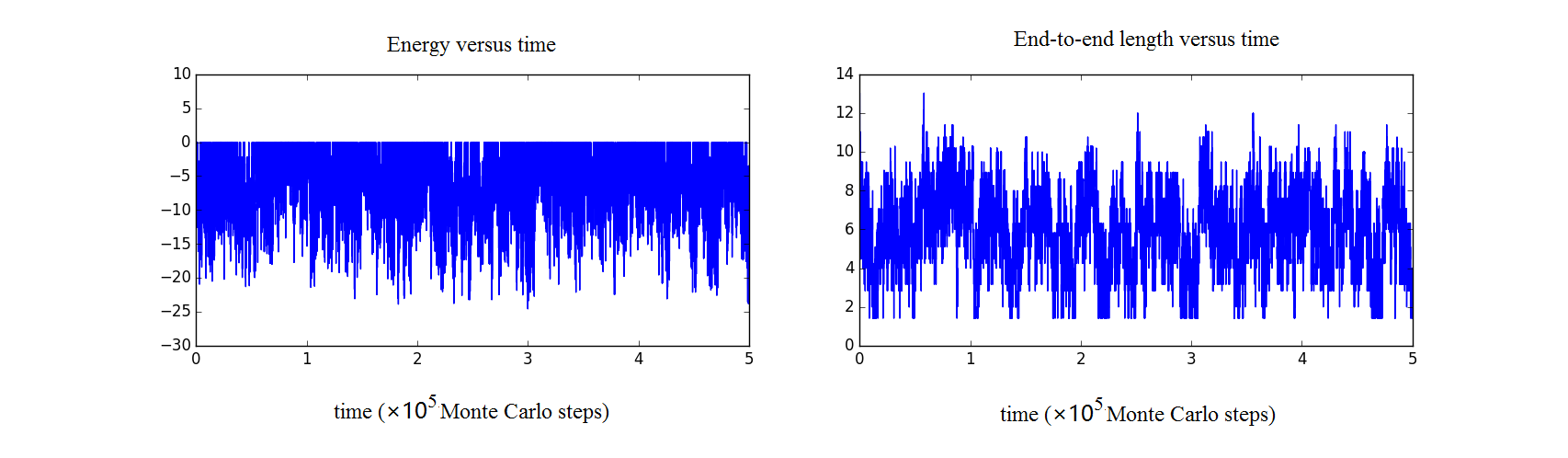
Figure final.2 15个氨基酸构成的多肽链的能量(左)和端点间距离(右)随时间的变化关系。图中温度为, 分子间相互作用 与图(2) 相同
讨论
蛋白质的计算是一项计算量十分浩大的工作,由于作者计算机的计算能力限制,在生物体中,能承担生命活动的蛋白质,如离子泵、蛋白质类激素、酶等,往往由数百个氨基酸数个三级结构在三维空间构成三级结构,数个三级结构形成最终的蛋白质。可以想见,对这样的结构进行模拟非一般个人电脑能够完成。而我们在此讨论的都是二维平面内结构十分简单的短链多肽,程序的蒙特卡罗模拟步数,以及讨论涉及的情况数均与参考文献[7] 有所差距。原计划试用不同形式的J矩阵对多肽链折叠进行模拟,但是由于程序复杂度而作罢。另外,在参考文献中给出了不同温度下经过多次蒙特卡洛模拟平均后的体系能量和端点间距离,这两个物理量均随着多肽链温度升高而增加。但是根据作者的模拟,这两个量均呈现出较大范围的波动,且与温度没有明显的相关关系,所以没有呈现在这份报告中。经过分析之后,认为可能的原因有三个。(1) 由于计算量不足,导致的统计均值的标准差较大。(2) 选用的J矩阵和多肽链上每个位点的氨基酸种类与参考文献[7]不同。(3) 程序实现过程中数据结构的错误。由于程序由python实现,在这一编程语言中,当使用一个变量为一个新变量赋值时,实际的过程是将新变量名作为指针指向了原有变量。所以对新变量的改动都会使得旧变量一并改动。这一问题的解决方法是在使用新变量的时候将原有变量进行复制并将副本赋给新变量。我们根据此方法进行了修改,但是结果和修改之前的程序没有明显区别。由于时间仓促,程序较长,无法在程序确认正确的情况下撰写报告,也无法提供更多正确且有意义的成果,请老师原谅。本程序已全部开源在Github网站,欢迎感兴趣的同学一同寻找程序中可能出现的问题。
补充材料
本程序已全部开源在Github网站(https://github.com/ShixingWang/computationalphysics_N2013301020050)
参考文献
Francis Crick. Ideas on protein synthesis. U.S. National Library of Medicine, 1956.
Francis Crick et al. Central dogma of molecular biology. Nature, 227(5258):561–563, 1970.
《生物(必修二)遗传与进化》, 高等教育出版社,2007.
浙江大学普通化学教研组, 《普通化学(第五版)》,高等教育出版社,September 2002.
C. B. Anfinsen. Principles that govern the folding of protein chains. Science, 181(4096):223–30, 1973.
Reif. Fundamentals of Statistical and Thermal Physics. Waveland Pr Inc, 2008.
Hisao Nakanishi Nicholas J. Giordano. Computational Physics. Tsinghua University Press, second
edition, December.
