View this in Github
View this in "作业部落"

Exercise 14: Two Wavepackets

---

王世兴
2013301020050

---

Problem 6.6
An important feature of a linear equation is that the sum of two solutions is also a solution. One consequense of this is that two wavepackets will travel independently of each other. An especially clear way of demonstrate this is to set up a string with an initial profile such that there are two Gaussian wavepackets located at different places on the string. These wavepackets (or components of them) may then propagate toward each other and collide. Show that these wavepackets are unaffected by these collisions. That is, show that two such wavepackets pass through each other without changing shape or speed.

---

Abstract

Wave propagating along a string is an interesting question involving the time evolution of a dynamical system. The liearity is confirmed in the program that two Gaussian waves propagates independently with their speed and shape unruffled.

Background

Superposition of Linear Equations

In mathematics, a linear map or linear function f(x) is a function that satisfies the following two properties:

Additivity: f(x + y) = f(x) + f(y).
Homogeneity of degree 1: f(αx) = αf(x) for all α.

The homogeneity and additivity properties together are called the superposition principle. It can be shown that additivity implies homogeneity in all cases where α is rational; this is done by proving the case where α is a natural number by mathematical induction and then extending the result to arbitrary rational numbers. If f is assumed to be continuous as well, then this can be extended to show homogeneity for any real number α, using the fact that rationals form a dense subset of the reals.

Wavepacket

In physics, a wave packet (or wave train) is a short "burst" or "envelope" of localized wave action that travels as a unit. A wave packet can be analyzed into, or can be synthesized from, an infinite set of component sinusoidal waves of different wavenumbers, with phases and amplitudes such that they interfere constructively only over a small region of space, and destructively elsewhere.[1] Each component wave function, and hence the wave packet, are solutions of a wave equation. Depending on the wave equation, the wave packet's profile may remain constant (no dispersion, see figure) or it may change (dispersion) while propagating.

Main Features of the Codes

The dynamic function of the string with ends fixed is

$$\frac{\partial^2y}{\partial t^2}=c^2\frac{\partial^2y}{\partial x^2}$$
to realize this algorihtm on pyhton we need the discrete form of the equation. We use i as the index for different position on the string and n as the index of time.
$$y(i,n+1)=2(1-r^2)y(i,n)-y(i,n-1)+r^2[y(i+1,n)+y(i-1,n)]$$
where $r=c\Delta t/\Delta x$ is a parameter describing the relative magnitude of the time step length and segment step length. The best choice of r is 1. Smaller r will raise extra pertubation while larger r can hardly yield results.

numpy Functions

numpy is a Python package famous for scientific computation. It provides a fine data strcture numpy.ndarray together with costomized functions simplifying computations. For example, we need a discrete exponential function, with math package, we need a list and use for cycle to change the value of each element of the list. While in numpy, things are much easier.

self.X=np.linspace(0,length,self.i,endpoint=True)
self.Y0=np.exp(-k*(self.X-x0)**2)

Initial Conditions

Gaussian equations are chosen as the initial condition, that is, $y(i,n=0)$. From the equation above $y(i,n=-1)$ is needed. Here we assume that the string before the instant the program begins has the same initial condition, i.e. $y(i,n=-1)=y(i,n=0)$

Boundary Conditions

In the program we used the fixed boundary condition

$$y(0,n)=y(M,n)=0$$
Two methods were conjured up to raelize this conditon. The first is to calculate the program for the whole string and after each cycle we change the value to be zero on both ends. This was used in the codes of last exercise, but there were so many bugs that I finally aborted the code. In this code I took care to calculate from the second segment to the second last segment of the string. It works fine.

Save Figures in .gif Form

The best way to show the result of the code is to save as the .gif figure. But matplotlib does not offer convenient gif figure saving, so we need to download and install ImageMagick. Some tutorials are given below.

利用Matplotlib和ImageMagick制作gif动画
使用Matplotlib和Imagemagick实现算法可视化与GIF导出

Results

First we use a initial condition that a Gaussian function on the string with its peak at 0.3 m form the left end of the string.

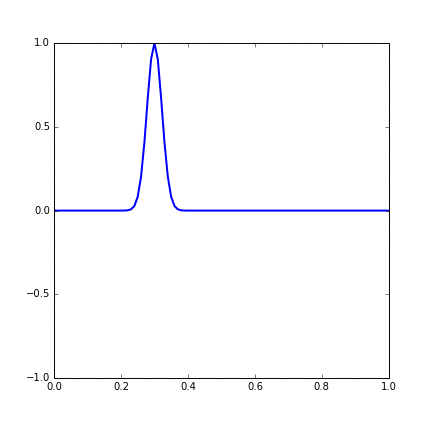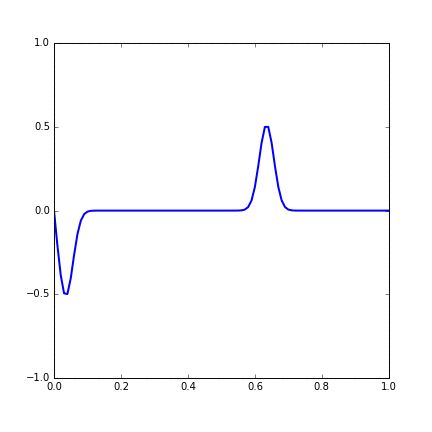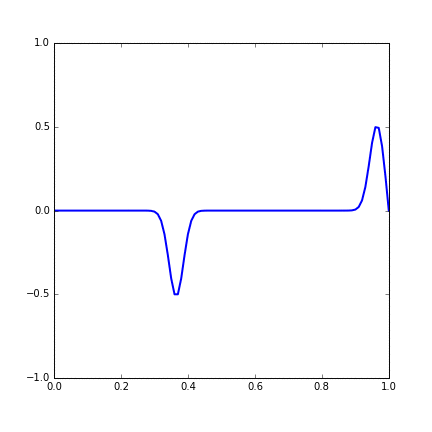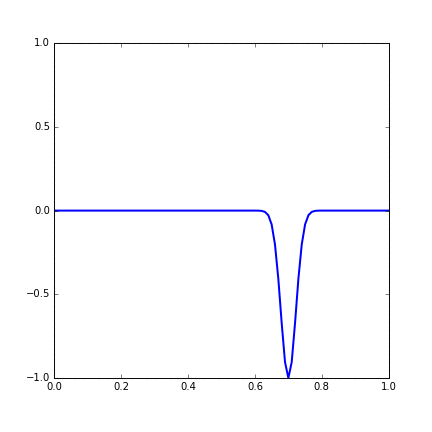
Figure 14.1 Dynamic figure of single Gaussian initial function.

Then to test the conditions required by the question by adding another Gaussian function with its peak at 0.7m. The initial condition is shown below.

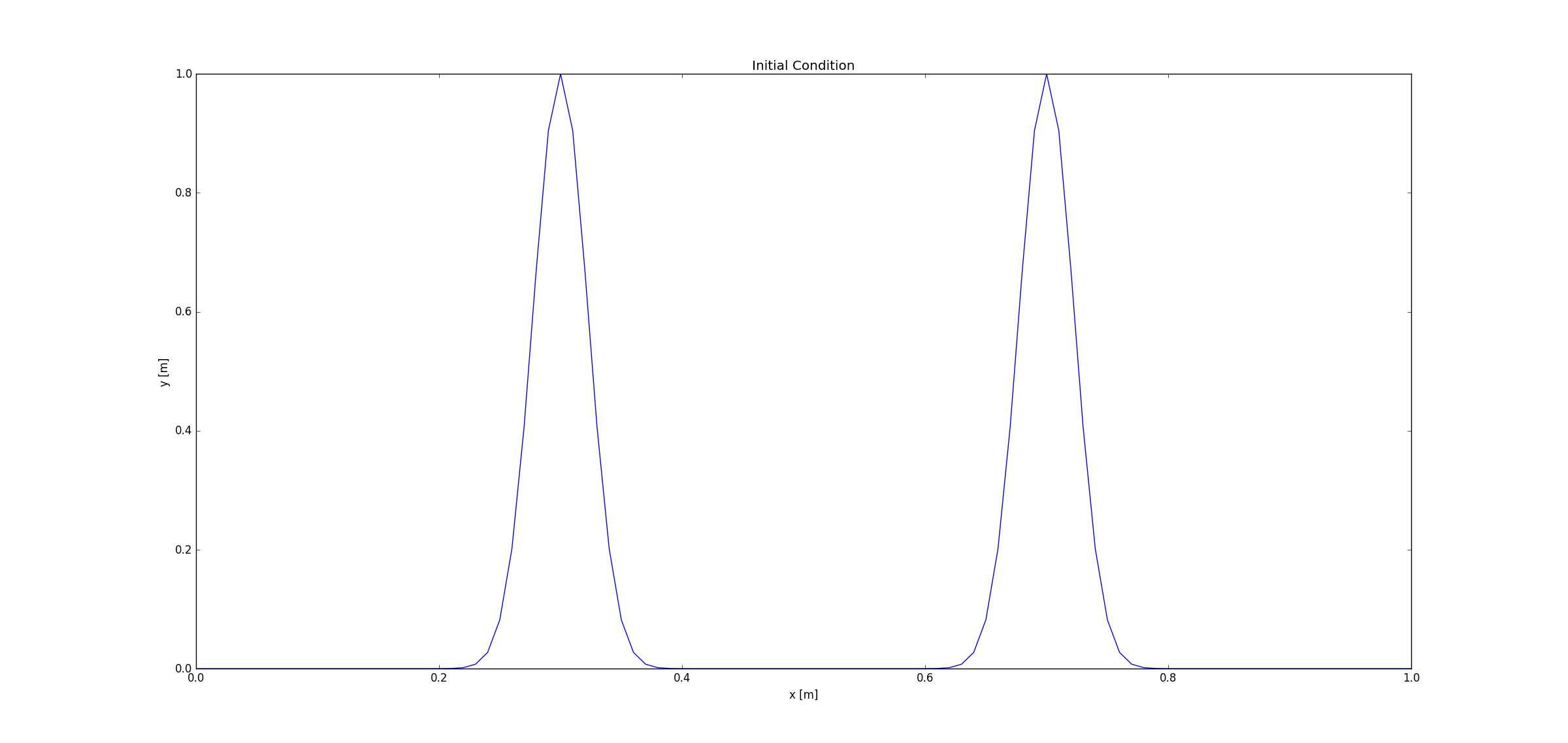
Figure 14.2 Initial condition of two Gaussian functions.

And the development of the system with time is shown in the gif. We can see that two wavepackets pass through each other without changing shape or speed.

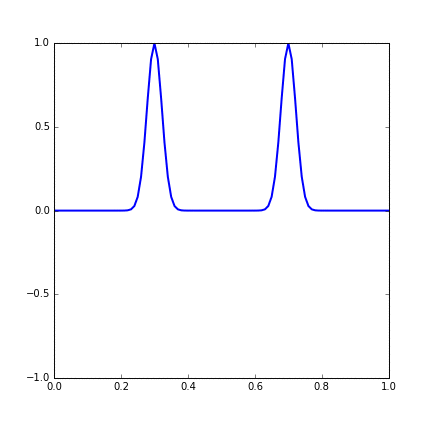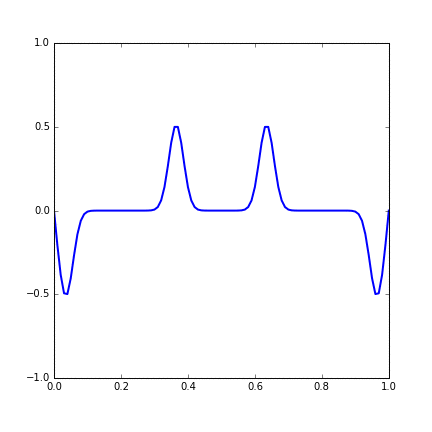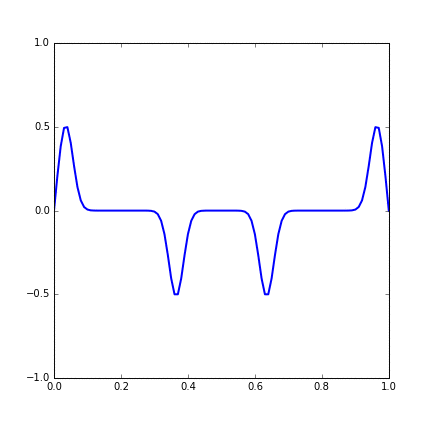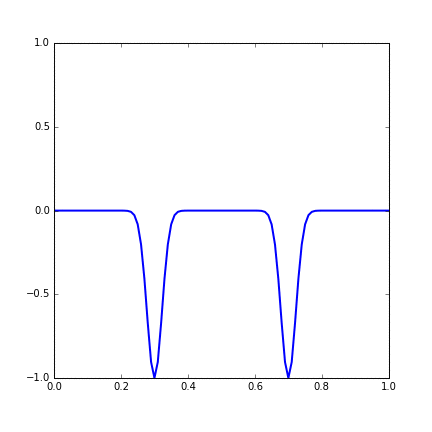
Figure 14.3 Time evolution of a string with two Gaussian wave initial condition.

Reference

1. Linearity. (2016, May 11). In Wikipedia, The Free Encyclopedia. Retrieved 10:35, May 31, 2016, from https://en.wikipedia.org/w/index.php?title=Linearity&oldid=719783892

2. Wave packet. (2016, April 13). In Wikipedia, The Free Encyclopedia. Retrieved 10:18, May 31, 2016, from https://en.wikipedia.org/w/index.php?title=Wave_packet&oldid=715077854

感谢陈锋同学的ImageMagick运行环境得到的动态图