View this in Github.
View this in "作业部落"

Exercise 7: Backspin of Baseball and 3D Cannon Shell

王世兴
2013301020050

• Problem 2.19: Backspin of Baseball
• Visualize the cannon shell or baseball with VPython

Abstract

Baseball is a sport of great interest for physics for its appropriately complexity of combining the elastic dynamics of bats, fluid dynamics of the ball and so on. [1] VPython has been introduced in early exercises to visualize results. In the report a discussion of the backspin of the baseball is presented as level 1 and an emendation of Exercise 6 [2] concerning Coriolis effect is made, with 3D plot attribute inside the module realized with VPython.

Background

Bernoulli's principle and Magnus Effect

Bernoulli's principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid's potential energy. [3] The principle is named after Daniel Bernoulli who published it in his book Hydrodynamica in 1738. [4] This principle is often demonstrated as the following equation

$$p+\frac{1}{2}\rho V^2+\rho g h = const.$$
But we should be careful since this equation is based on the conseravtion of mechanical energy, thus is valid only when fluid of interest is inviscid and uncompressable.

Now we consider a special case of such principle, a spinning in a fluid.

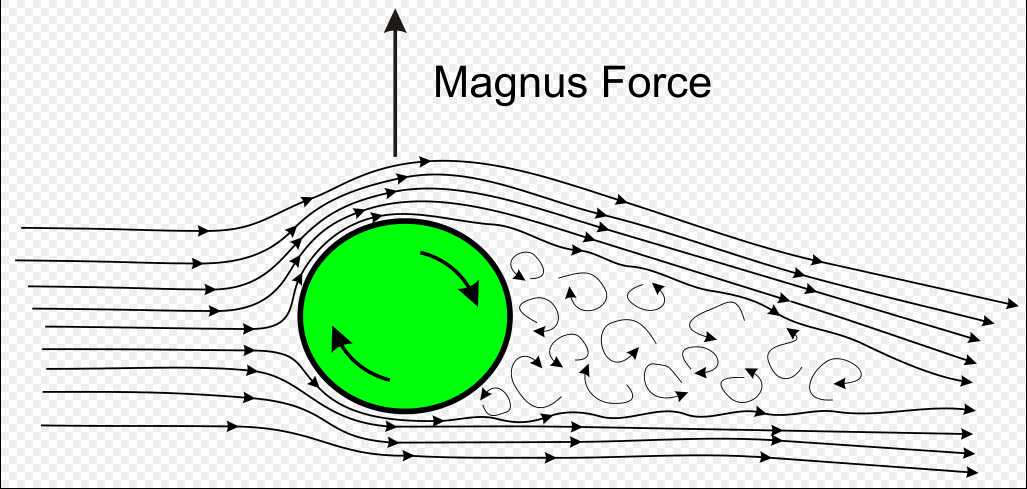
Magnus Effect [5]

In terms of ball games, topspin is defined as spin about an axis perpendicular to the direction of travel, where the top surface of the ball is moving forward with the spin. Under the Magnus effect, topspin produces a downward swerve of a moving ball, greater than would be produced by gravity alone, and backspin has the opposite effect. [5]

Several ways can help comprehend the mechanism. First, the back spin makes the air below flow with a lower velocity than the air above, thus a pressure variance is made. Also, the faster the air moves, the more likely turbulent flow forms, making an extremely low pressure above the ball, making it fly higher and longer.

Further research reveals that under ordinary cases, the force caused by Magnus Effect can be expressed as

$$\vec F_{Magnus}=S_0\vec\omega\times \vec v$$
In the backspin cases, since the spin vector is perpendicular to the plane of the gravity and the velocity vector, no Magnus Effect is shown in this direction, the form of force becomes
$$\begin{array}{ll}F_x=-\frac{S_0\omega v_y}{m}\\F_y=\frac{S_0\omega v_x}{m}\end{array}$$

Air Drag as a Function of Velocity

In the last program we have assumed that the air drag is propotional to the square of velocity in the form $F=-B_2v^2/m$. However, in realistic cases the drag coefficient is a function of the velocity. At low sppeds, the coefficient is close to 1/2, However as the speeds increases, is drops substaintially. As an approximation we use the analytical function

$$\frac{B_2}{m}=0.0039+\frac{0.0058}{1+e^{(v-v_d)/\Delta}}$$
where $v_d=35m/s$ and $\Delta=5m/s$, the numbers above are in the SI unit.

Results

Level 1: Problem 2.19

Source code
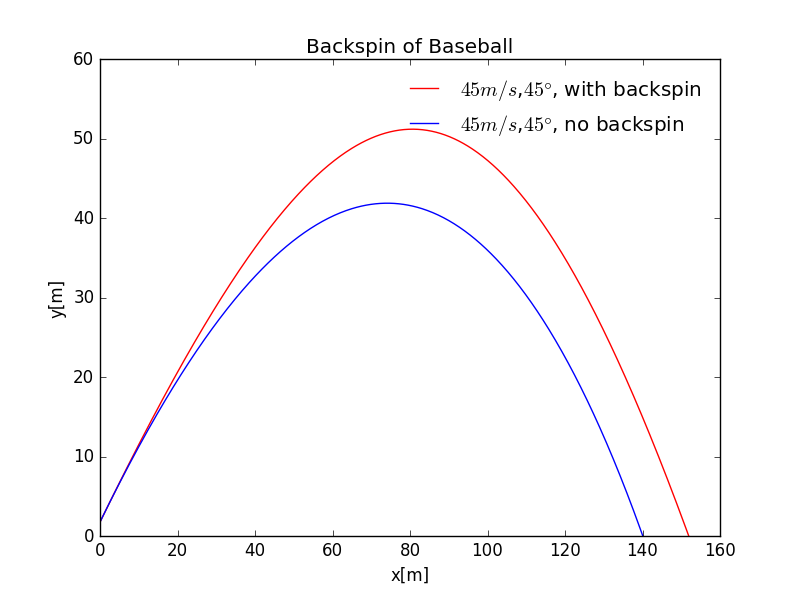
In the code we treat the air drag coefficient as a function of velocity and compare the effect with that without backspin. Under the initial condition given (a velocity of 45 m/s and shooting angle of 45 degrees), the baseball with backspin has a higher maximum height and a longer range.

Level 2: Visualization

Source code
In this program we use the Coriolis force in the form of the equations provided in the Background section and the air drag same as those in Exercise 6

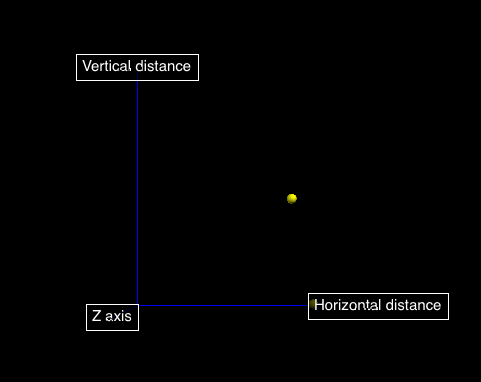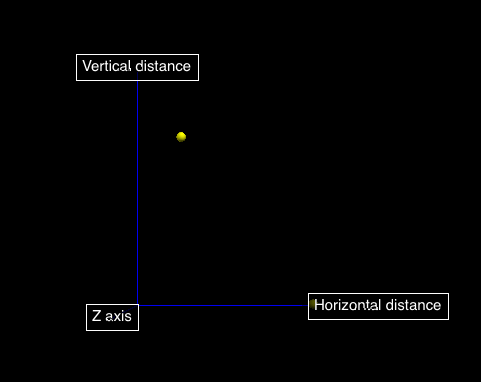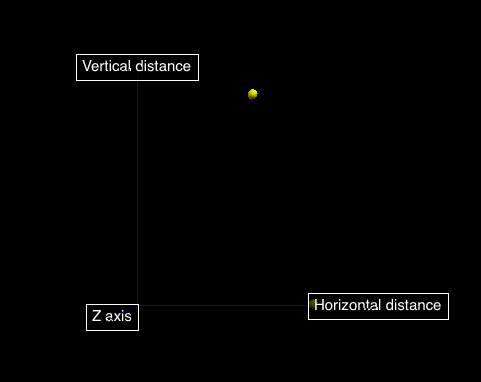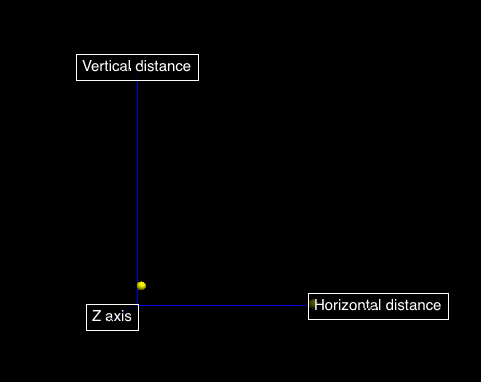
And we used python-visual to visualize the motion of the cannon shell. The animation of the shell is realized through the internel attribution sphere.velocity where we use the velocity calculated in the internal function cannon0.fly().

One thing that need notice is that the default coordinate in python-visual is the one with y-axis as the axis showing the altitude, and x, y, z forms a right-handed frame. However, in this program I used the conventional one in which z-axis scales the altitude. This is only a rotation of coordinates.

Acknowledgement

• 本次level 2结果来自吴威鹏同学的能正常运行python-visual的ubuntu虚拟机文件，在此表示感谢；同时感谢陈锋同学分享这一虚拟机文件

• 感谢陈锋同学在我的电脑无法运行python-visual时帮忙运行并修改错误。

Reference

• [1] Adair, R.K. The Physics of Baseball. Harpercollins. Jan, 1990

• [2] Shixing Wang. Exercise 6: Cannon Shell. Github, https://github.com/ShixingWang/computationalphysics_N2013301020050/blob/master/Reports/Exercise6.md, April 10, 2016

• [3] Wikipedia contributors. "Bernoulli's principle." Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 31 Mar. 2016. Web. 10 Apr. 2016.

• [4] "Hydrodynamica". Britannica Online Encyclopedia. Retrieved 2008-10-30.

• [5] Wikipedia contributors. "Magnus effect." Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 16 Jan. 2016. Web. 10 Apr. 2016.