View this in Github.
View this in "作业部落"

Exercise 8: Problem 3.4 & 3.5 - Anharmonic Ocsillator

---

王世兴
2013301020050

---

Problem 3.4 [1]
For simple harmonic motion, the general form of the equation of motion is

$$\frac{d^2x}{dt^2}=-kx^{\alpha}$$
with $\alpha=1$. Begin by writing a program that uses the Euler-Cromer method to slve for x as a function of time with $\alpha=1$. Show that the peroid of the oscillations is independent of the amplitude of the motion. Then extend your program to treat cases with $\alpha=3$. This is an example of an anharmonic oscillator. Calculate the peroid for a few amplitudes. Give an intuitive explanation of why the perid becomes longer when the amplitudes decrease.

---

Problem 3.5 [1]
Analytically obtain the peroid of oscillation for general values of $\alpha$ in terms of certain special functions. Describe how the relationship between the peroid and the amplitude depends on the value of $\alpha$. Give a physical interpretation to the finding.

---

Abstract

The assumption of simple pendulun that the restoring force is proportional to the angular displacement is sometimes superficious. [1][2] In peroidical processes, the Euler method may prove inappropiate for the accumulation of errors. In this program the Euler-Cromer method is used t simulate an anharmonic pendulum domineered by a force as a polynomial function of angular displacement. The analytical solution is given for comparison. Various values of amplitude are tested, proving that the dependence of peroid on the amplitude. Intuitive explanation for the behavior of the peroid and amplitude is provided.

Background

Oscillators

A pendulum is a weight suspended from a pivot so that it can swing freely. [2] If the angle from the position of the weight to its equilibrium positon is small, we can equte describe the force with linear model as an approximation of sinusoidal relation, which means

$$ml\frac{d^2\theta}{dt^2}=-mg\,\text{sin}\theta\approx -mg\theta$$
and the solution has a sinusoidal form
$$\theta(t)=\theta_0(\Omega t+\phi)$$
And when the force is a polynomial function of the angular displacement, interesting attributions will show up.
$$\frac{d^2\theta}{dt^2}=-k\theta^{\alpha}$$
More detail will be discussed in the remaining of this report.

Euler-Cromer Method

The Euler method has been proven powerful and time economical in calculating the motion of projectile motion and its modifications. [3][4] However, since we have ignored the terms greater than the differentiation higher than the second order, when dealing with periodical processes, such error accummulates in every cycle and the program finally crushes down. In terms of physics, the energy of the system is not conserved.

The solution is the Euler-Cromer method, which only differs slightly. We use the old $\theta$ and $\omega$ to calsulate the new ones after a time intervel, while in the Euler-Cromer method we use the old $\theta$ and new $\omega$. The energy is conserved over each complete peroid of motion, avoiding the problems in Euler algorithms.

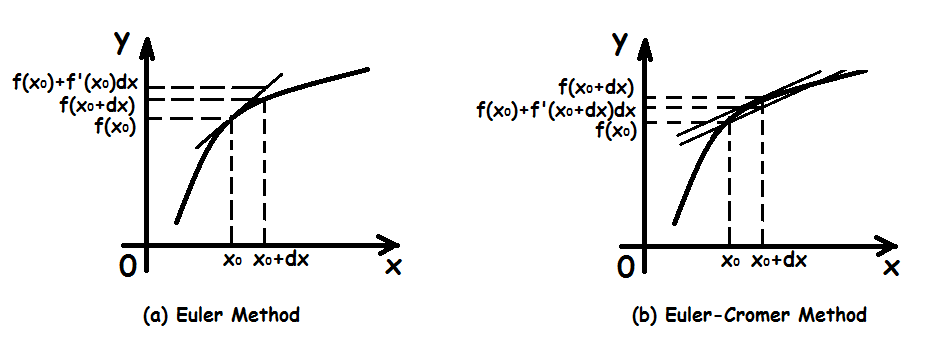
Schematic diagram for Euler method (a) and Euler-Crome method (b).

For a second-order ordinary equation

$$\frac{d^2\theta}{dt^2}=f(\theta,t)$$
we solve this by introducing $\omega(t)=d\theta(t)/dt$ and
$$\begin{array}{ll}\omega(t+dt)&=\omega(t)+f(\theta,t)dt\\\theta(t+dt)&=\theta(t)+\omega(t+dt)dt\end{array}$$

Results

Harmonic and Anharmonic Oscillation

With $\alpha=1$, the equation degenerates back to the simple harmonic oscillation. This is also a test for algorithm's validity.

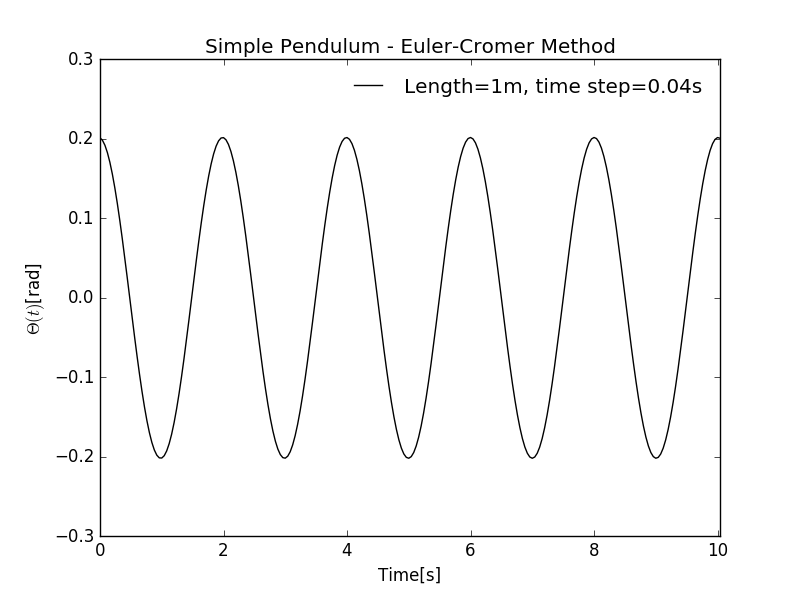
Simple Harmonic Pendulum as a particular case of anharmonic oscillation, with k=9.8, dt=0.04

By comparison with the Figure 3.3 on Reference [1], we can see our program have the same result with that in the textbook, ensuring us to go on with this program. And a comparision between harmonic ($\alpha=1$) and anharmonic ($\alpha=3,5,7$) is given. Different alpha values give the same amplitude but different periods. The larger the value of alpha, the larger the period is.

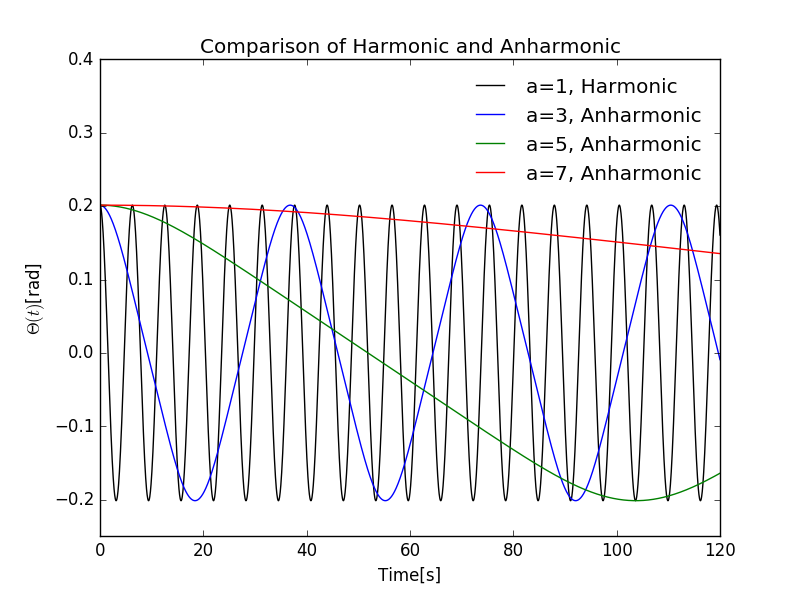
Comparison of harmonic and anharmonic oscillation, with k=1, dt=0.04, time=120s

Dependence of Peroid on Amplitude

To calculate the period of the ocsillator we add a function period(self) inside the class pendulum. This function should be modified since the length to judge whether $\theta(t)$ reaches its maximum should be modified for various amplitudes. And the plot is given and relationship between amplitude and period are listed in the chart below.

Amplitude(rad)	Period(s)	Theoretical Period(s)
0.2	36.831	37.082
0.4	18.021	18.541
0.6	11.524	12.361
0.8	7.937	9.270
1.0	4.721	7.417

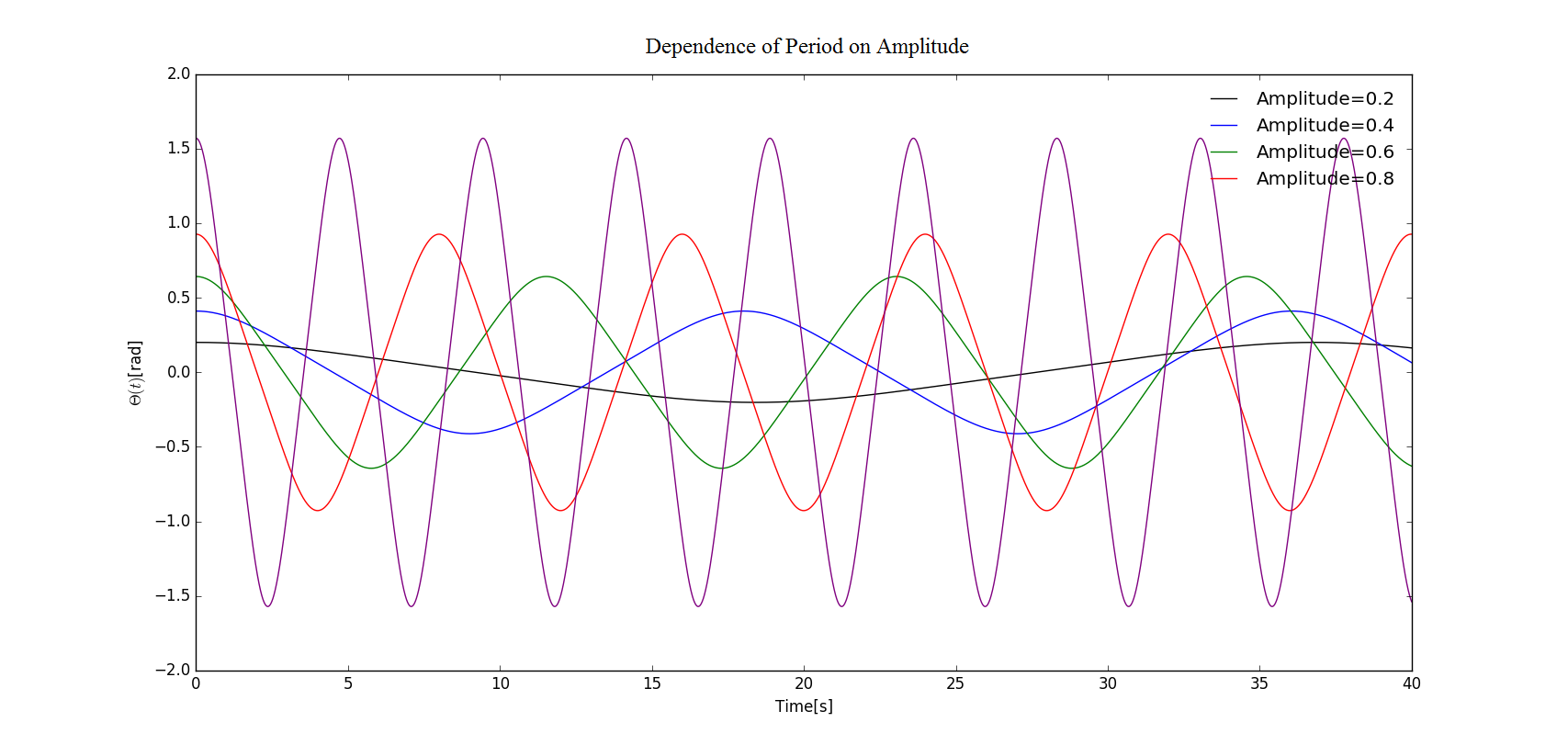
Figure and chart of the relationship between amplitude and period, with dt=0.001s, time=40s, k=1, $\alpha$=3

Intuitive Explanation

From the form of the force, at a small angular displacement, which means $\theta<<1$, we have $\theta^{\alpha}<\theta$ for $\alpha>1$. This means at a given position, the restoring acceleration on the mass point in the anharmonic oscillator is smaller than the harmonic case, making the period longer than the harmonic oscillator.

Analytical Solution of Anharmonic Oscillation

First a mathematical trick should be introduced to derive a relationship between angular velocity and angular displacement.

$$\frac{d^2\theta}{dt^2}=\frac{d}{dt}\frac{d\theta}{dt}=\frac{d}{d\theta}\left(\frac{d\theta}{dt}\right)\frac{d\theta}{dt}=\omega\frac{d\omega}{d\theta}=-k\theta^{\alpha}$$

And we multiply $\omega=d\theta/dt$ on both sides of the equation,

$$\frac{1}{2}\frac{d\omega^2}{dt}=-\frac{k}{\alpha+1}\frac{d\theta^{\alpha+1}}{dt}$$

According to Reference [5], the analytical solution of period could be given by inverting the equation of angular velocity

$$\frac{dt}{d\theta}=\frac{1}{\omega}$$
The period should be integration of time [6]
$$\begin{array}{l}T&=t(\theta_0\to0\to-\theta_0\to0\to\theta_0)=4\int_0^{\theta_0}\frac{dt}{\omega}\\ \quad & =-4\sqrt{\frac{\alpha+1}{2k}}\int_{x_0}^0\frac{dx}{\sqrt{x_0^{\alpha+1}-x^{\alpha}}} \end{array}$$

When $\alpha$=3, $T\approx7.4163\frac{1}{x_0\sqrt{k}}$

By comparison with the numerical result, this algorithm performs well when the angular displacement is relatively small, while the results deviate from the analytical result as alpha increases. This means although Euler-Cromer algorithm could ensure the conservation of energy in every whole cycle, the error should still be paid attention. But luckily when the angular displacement is relatively large, the assumption of the anharmonic oscillation model should also be modified.

Reference

1. Giodano, N.J., Nakanishi, H. Computational Physics. Tsinghua University Press, December 2007

2. Wikipedia contributors. "Pendulum." Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 10 Mar. 2016. Web. 16 Apr. 2016.

3. Shixing Wang. Exercise 6: Cannon Shell. Github, https://github.com/ShixingWang/computationalphysics_N2013301020050/blob/master/Reports/Exercise6.md, April 16, 2016

4. Shixing Wang. Exercise 7: Backspin of Baseball and 3D Cannon Shell. Github, https://github.com/ShixingWang/computationalphysics_N2013301020050/blob/master/Reports/Exercise7.md, April 16, 2016

5. Wikipedia contributors. "Pendulum (mathematics)." Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 7 Apr. 2016. Web. 17 Apr. 2016.

6. Chen Feng. "Chapter 3 Problem 3.4". 作业部落， https://www.zybuluo.com/355073677/note/345564, April 17, 2016.