view this on "作业部落"

Exercise 6： Crazy Cannon _(:-↙∠)_

Abstract

Projectile motion is one of the most common movement in daily life, and is said to have inspired Issac Newton of the gravitation laws.[1] Strictly speaking, a projectile motion is defined as one under the action of gravity only,[2] while in reality modificaitons are in need due to the influence of air. Various conditions about the air drag force are discussed. Under the condition of real life parameters, the uniform air drag limits the rage most dramatically, while (下面讲对最远发射角度的改变) Finally a "stochastic cannon" with errors in the initial velocity, the firing angle and air drag force is presented. An algorithm is given to attain the best velocity and angle to hit the target.

Background

Projectile Motion and Modifications

A projectile motion is defined as "a form of motion in which an object or particle (called a projectile) is thrown near the earth's surface, and it moves along a curved path under the action of gravity only."[2] This definition is an ideal model while in real life one can be assumed as a projectile motion if gravity takes the domineer significance.

According to Newton's Law, $F=ma$, and the acceleration in horizentaal and vertical direction

$$\begin{array}{ll}a_x=0\\a_y=-g\end{array}$$
And since $a=\frac{d^2x}{dt^2}=\frac{d}{dt}(\frac{dx}{dt})=\frac{dv}{dt}$
$$\begin{array}{llll}v_x(t)=v_0\ cos(\theta)\\v_y(t)=v_0\ sin(\theta)-gt\\x(t)=v_0t\ cos(\theta)\\y(t)=v_0t\ sin(\theta)-\frac{1}{2}gt^2\end{array}$$
This has inspired us to convert two simultaneous second-order ordinary differential equation into four first-order equations by introducing velocity as a function of time.
And if time is eliminated from the equations above we get
$$y(x)=tan(\theta)\cdot x-\frac{g}{2v_0^2cos^2(\theta)}x^2$$

When concerning about the air drag force, we assume that the impedence comes from the work needed to accelerate the air occupied in the volumn that the shell will sweep in unit time. So it is propotional to the density of air and the square of the velocity of the shell.

$$F_{drag}=-\frac{1}{2}C\rho Av^2$$

Air Drag and Rifling

As is mentioned above and will be discussed thoroughly in our codes, air drag force plays a critical role in the shells' trajactory. But engineers have come up ideas of rifling to fight against such impedence.

Rifling is a series of spiral line inside the pipe of fire guns like rifles and cannons.[3] When the shells get out of the pipe pushed by the gunpowder at the end of the bore of a gun, the high temperarure will inflate the shell making it rub with the rifling and spin. Such spin motion will effectively reduce the air drag force.

Air Density Distribution

In the first section we gave the form of air drag force under simple assumptions. Now we come to a stage a little more complex. The force is sill propotional to the density of air. However, the density of air is a decreaseing function of altitude.

Isothermal Condition

The simplest model is to treat the atmosphere as an ideal gas with constant temperature. For a thin air layer with area S and thickness dz, we have

$$\begin{array}{ll}p(z+dz)S+\rho gSdz=p(z)S\\pV=\rho RT\end{array}$$
And the solution: [4]
$$\begin{array}{ll}p(y)=p(0)e^{-mgy/k_BT}\\\rho=\rho_0e^{-y/y_0}\end{array}$$
where $y_0=k_BT/mg\approx1.0\times10^4m$, and $\rho_0$ is density at sea level.

Adiabatic Condition

The isothermal model is not quite realistic for it cannot explain the rapid temperature decrease over a small scale of altitude. Another model treats air as heat pool with very slow convection. [4][5][6]

$$\rho=\rho_0(1-\frac{ay}{T_0})^\alpha$$
Both the isothermal and adiabatic condition gives the similar form modification of air drag force
$$F^*_{drag}=\frac{\rho}{\rho_0}F_{drag}(y=0)$$

Coriolis Force

The inertial frame of reference is the essential and critical concept in Newtonean Mechanics. Only in an inertial frame can the Newon's First Law be satisfied. But luckily, in an non-inertial frame the problem can br solved by the introduction of an imaginary inertial force. And Coriolis Force is such a force in a rotation frame.

Italian scientists Giovanni Battista Riccioli and his assistant Francesco Maria Grimaldi described the effect in connection with artillery in the 1651, and Gaspard-Gustave Coriolis published a paper in 1835 on the energy yield of machines with rotating parts discussing this extra acceleration. [7] The form of Coriolis force is propotional to the cross product of the velocity of the object and the rotation angular velocity of the frame of reference.

The rotation of Earth is so slow that we can ignore the effect of Coriolis effcet. However, for some guns that possess really long range, the effect of the Coriolis effect must be taken into consideration, such as the Paris Gun.

The Paris Gun (German: Paris-Geschütz) was the name given to a type of German long-range siege gun, several of which were used to bombard Paris during World War I. The shells of such guns were first human-made objects that reached stratosphere. The Paris gun was used to shell Paris at a range of 120 km. The distance was so far that the Coriolis effect was substantial enough to affect trajectory calculations. After World War I, the gun was firbidden by the Treaty of Versailles, but under the funding of Nazi, Krupp continued the study of such weapons and K12 Gun was deployed in the World War II.

In the picture is the K12 gun set to the attack position.

Results

Trajectory for Various Cannons

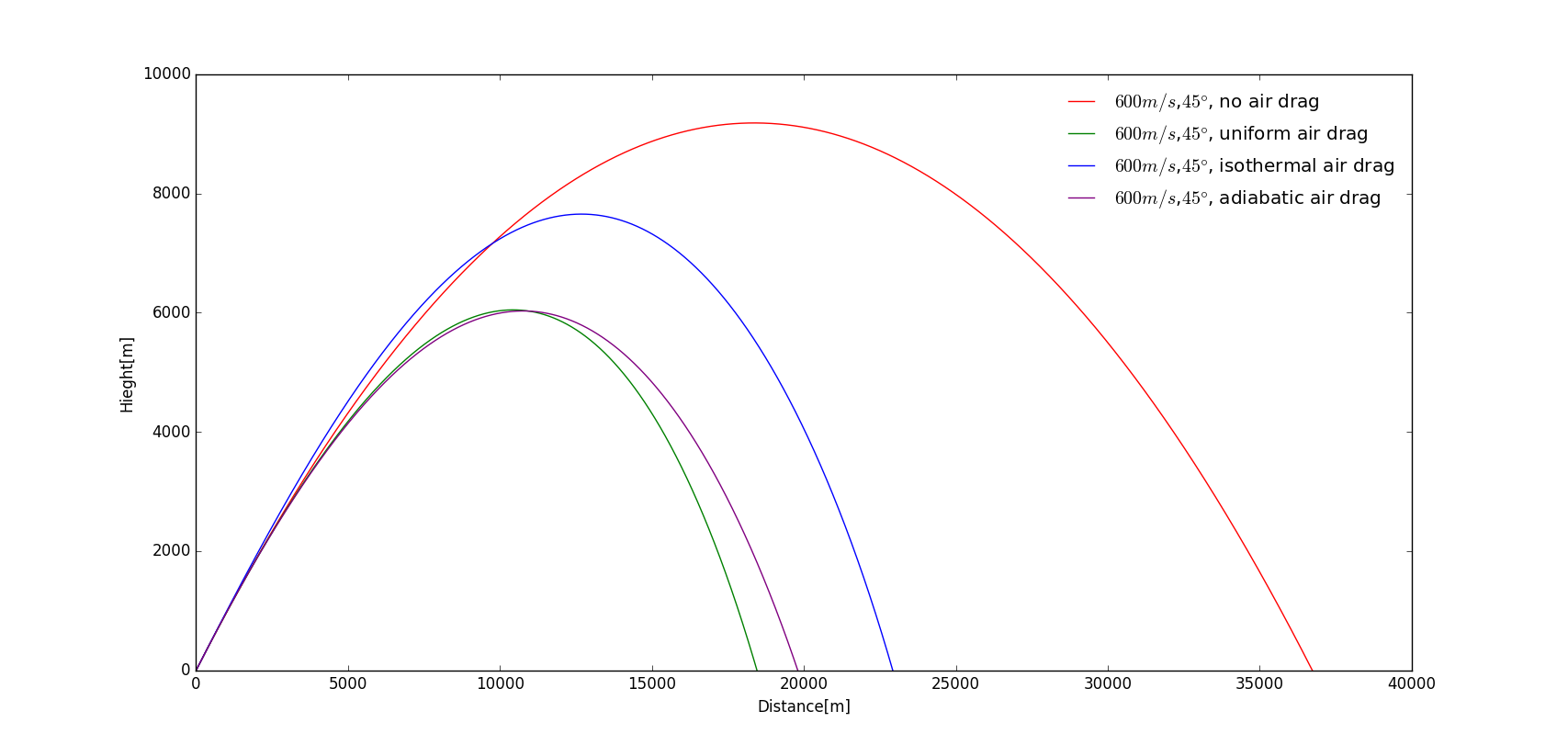
The figure above shows the trajectory with the initial velocity of 600m/s and initial angle 45 degrees.

The cannon with largest range is the one with no air drag, then isothermal air drag, adiabatic air drag, and finally uniform air drag.

Condition	Distance [m]	Relative Distance
No air drag:	36734.7	100%
Uniform air drag:	18459.2	50.5%
Isothermal air drag:	22927.0	62.4%
Adiabatic air drag:	19801.7	53.9%

As for the curve at the beginning, it is most noticable that the curve with isothermal air drag is even higher than that with no air drag. This is reasonable because the total external force in the isothermal condition that is vertical to the direction of the velocity is smaller than that with no air drag,

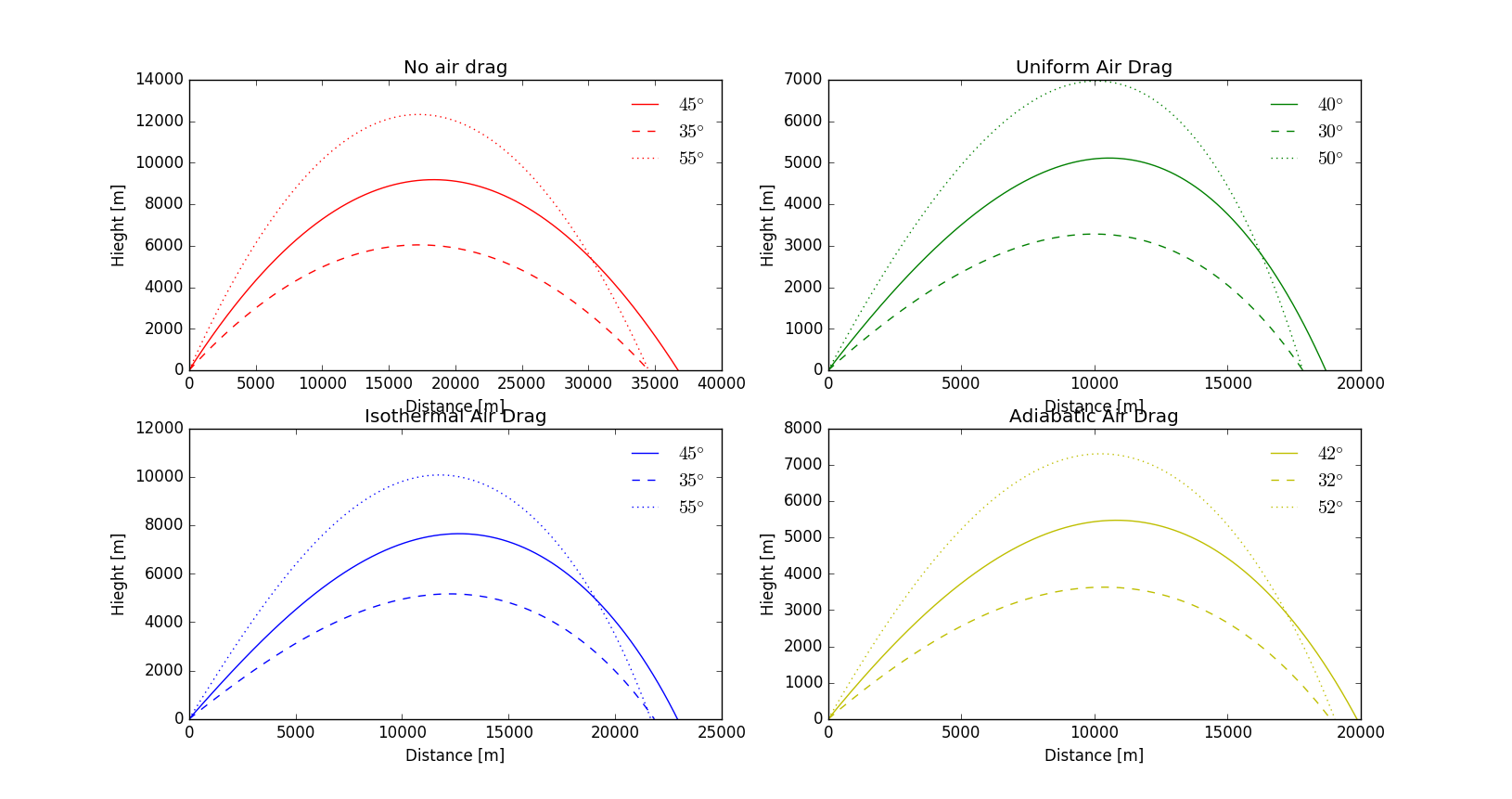
Angle Yielding the Largest Range

We used algorithems introduced in the Discussion section to obtain the angle that can yield the maximum range. And the result are listed below. The results may vary as parameters change and the effect of parameters are not listed due to the time complexity of cycle algorithms.

Condition	Max Angle [degree]
No air drag:	45.0
Uniform air drag:	40.0
Isothermal air drag:	45.0
Adiabatic air drag:	42.0

In the picture we plotted trajectories of the maximum angle and the ones having 10 degrees variance with the maximum angle.

Discussion: Main Features of the Codes

Object-Oriented Manner

Like the exercises before, [8][9] we wrote the codes in an obfect-oriented manner. The porjectile motion of shells are enclosured in a class connon0, with attribute fly(self) to calculate the trajectories, plot(self, color) to plot the trajextory and assign the color, distance(self) to return the final droppoint, height(self) to give the highest the shell could ever raech. Inside the class we defined an internal function F(vx,vy) to desecribe the air drag force, returning a 2-tuple with air drag force on x and y direction.

Level 1: Find Angle Yielding Largest Range

Source Code

We used a for cycle outside the class, to scan the angle 0.1 degree by 0.1 degree. This could be added into the class as an attribution but it has not been finished for the author could not spare time.

Level 2: Different Target Height

Source Code

The request of level 2 is to consider the height of the target may not be the same as the cannon. Ont only do we need to simply include one more variable, but the criteria for the end of cycle should be added a condition that the velocity must be negative (to ensure the program would not stop immediately if the target is over the cannon), but the correction for the x-coordinate of droppoint should be

$$x=\frac{(y_{n-1}-y_{final})x_n-(y_n-y_{final})x_{n-1}}{y_{n-1}-y_n}$$

Level 3: "Stochastic Cannon"

Source Code
To describe the error of initial velocity and shooting angle we need only change the initializing part __init__() with a probabilistic distribution by inducting the module numpy.random. As for the error of the air drag, I came up with an idea by introducing one more parameter in the F(self,vy,vy,y) attribute.

Future Directions

We have not been spared to discuss the relationship between the numerical solution and the accurate one. Also, the effect of different parameters are not clear partly due to the time complexity of the for cycle in the codes. Although the major part of code of Level 3 has been finished, the funciton to examine the distance between the target and the droppoint has not been finished.

Acknowledgement

The codes and report are finished by my self. Any corrections and suggestions will be appeciated.

Reference

1. Wikipedia contributors. "Isaac Newton." Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 31 Mar. 2016. Web. 2 Apr. 2016.
2. Wikipedia contributors. "Projectile motion." Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 5 Mar. 2016. Web. 2 Apr. 2016.
3. Wikipedia contributors. "Rifling." Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 1 Apr. 2016. Web. 4 Apr. 2016.
4. Giodano, N.J., Nakanishi, H. Computational Physics. Tsinghua University Press, December 2007.
5. Wikipedia contributors. "Atmospheric pressure." Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 31 Mar. 2016. Web. 4 Apr. 2016.
6. Wikipedia contributors. "Barometric formula." Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 25 Jan. 2016. Web. 4 Apr. 2016.
7. Wikipedia contributors. "Coriolis force." Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 1 Apr. 2016. Web. 4 Apr. 2016.
8. Shixing Wang. "Exercise 4: Double Decay" 作业部落， https://www.zybuluo.com/ShixingWang/note/321753，April 02, 2016
9. Shixing Wang. "Exercise 5: Problem 1.6 - Population Growth"作业部落， https://www.zybuluo.com/ShixingWang/note/326064，April 02, 2016