@CrazyHenry
2018-04-23T09:47:17.000000Z
字数 5063
阅读 2286
1-Flat.cpp
hhhhfaiss
- Author:李英民 | Henry
- E-mail: li
_yingmin@outlookdotcom- Home: https://liyingmin.wixsite.com/henry
- 转载请保留上述引用内容,谢谢配合!
| 方式 | 测试算法 | d | nb | xb | nq | xq | time |
|---|---|---|---|---|---|---|---|
| 无k-means,brute-force L2 distance,CPU | KNN(k=4) | 64 | 100000 | 100000xd | 10000 | 10000xd | 2345ms |
| 无k-means,brute-force L2 distance,CPU | KNN(k=4) | 256 | 100000 | 100000xd | 10000 | 10000xd | 6606ms(跟d呈线性关系?) |
| use k means,无PQ, CPU, nlist == 100, nprobe == 1(有错误) | KNN(k=4) | 256 | 100000 | 100000xd | 10000 | 10000xd | 145ms |
| use k means,无PQ, CPU, nlist == 100, nprobe == 11(正确结果) | KNN(k=4) | 256 | 100000 | 100000xd | 10000 | 10000xd | 1999ms |
| use k means,无PQ, CPU, nlist == 100, nprobe == 21(正确结果) | KNN(k=4) | 256 | 100000 | 100000xd | 10000 | 10000xd | 4825ms |
| use k means,无PQ, CPU, nlist == 100, nprobe == 31(正确结果) | KNN(k=4) | 256 | 100000 | 100000xd | 10000 | 10000xd | 6828ms |
接口:
faiss::IndexFlatL2 index(d); //类IndexFlatL2构造函数index.is_trained //a boolean that indicates whether training is requiredindex.ntotal //ntotal, the number of indexed vectors(特征向量的个数,nb)index.add(nb, xb); // add vectors to the index(database的vector矩阵xb和矩阵行数nb)index.search(nq, xq, k, D, I);//第一个参数本来应该是nq,第二个参数本来应该是xq,表示在database matrix中查找与k个与xq batches最近的特征向量
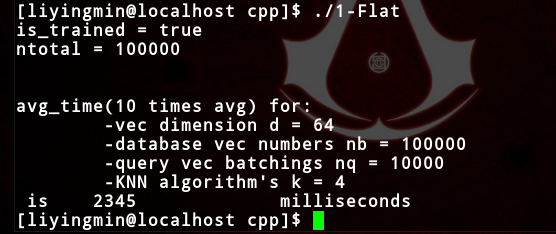
计时模块:
/** Author: yingmin.li** Date: 2018/4/21** Detail: add a timespan part for demo1**/#include <iostream>#include <string>#include <vector>#include <algorithm>#include <cstdio>#include <cstdlib>#include <chrono>#include <faiss/IndexFlat.h>//using std::using std::endl;using std::cout;//note: header file do not use usingint main() {int d = 64; // dimensionint nb = 100000; // database sizeint nq = 10000; // nb of queriesfloat *xb = new float[d * nb]; //database matrixfloat *xq = new float[d * nq]; //query matrixfor(int i = 0; i < nb; i++) {for(int j = 0; j < d; j++)xb[d * i + j] = drand48();xb[d * i] += i / 1000.; //just for fun!}for(int i = 0; i < nq; i++) {for(int j = 0; j < d; j++)xq[d * i + j] = drand48();xq[d * i] += i / 1000.;}faiss::IndexFlatL2 index(d); // call constructorprintf("is_trained = %s\n", index.is_trained ? "true" : "false"); //是否需要训练阶段index.add(nb, xb); // add vectors to the index,将database矩阵xb和database中特征向量的个数nb,给index对象printf("ntotal = %ld\n", index.ntotal); //返回database中特征向量的个数nbint k = 4; //KNN algorithm{ // search xqlong *I = new long[k * nq];float *D = new float[k * nq];auto begin_time = std::chrono::steady_clock::now();for(int i = 0; i < 10; ++i){index.search(nq, xq, k, D, I);}auto end_time = std::chrono::steady_clock::now();auto time_span = std::chrono::duration_cast<std::chrono::duration<long,std::ratio<1,1000>>>(end_time - begin_time);cout << endl << endl<< "avg_time(10 times avg) for:" << endl<< " -vec dimension d = " << d << endl<< " -database vec numbers nb = " << nb <<endl<< " -query vec batchings nq = " << nq << endl<< " -KNN algorithm's k = " << k << endl<< " is " << time_span.count() / 10 << " milliseconds" << endl;delete [] I;delete [] D;}delete [] xb;delete [] xq;return 0;}
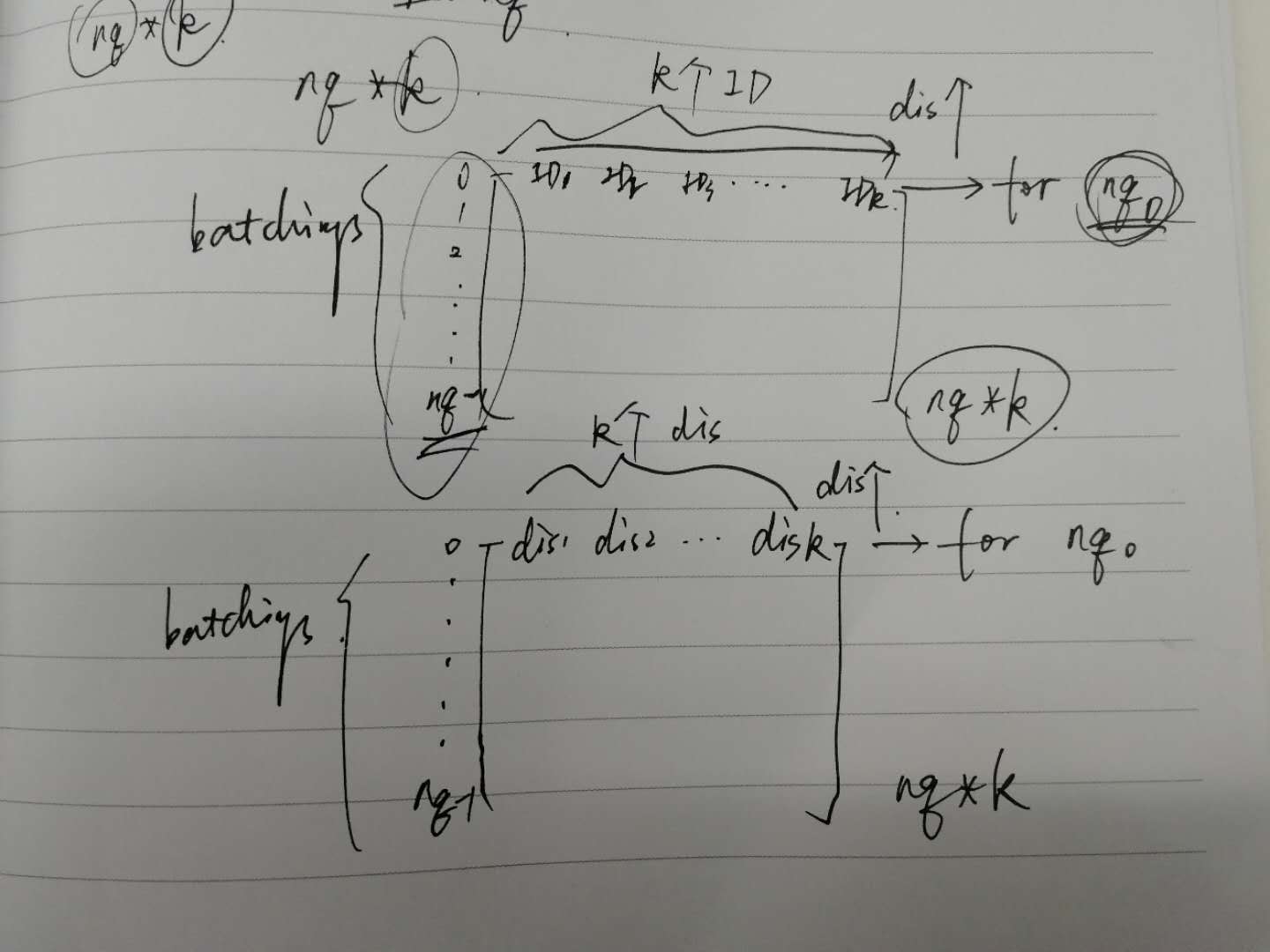
1.查询结果:
nq:输入待查特征向量的个数(行数),batchings
xq:待查数据矩阵 nq*d
xb:database的数据矩阵 nb*d
nb:database的特征向量的个数(行数)
int d = 64; // dimension
int nb = 100000; // database size
int nq = 10000; // nb of queries
2.数据分析:
输入待查矩阵xq = nq * d:32-bit floating point matrices, d = 64(特征向量的维度,可以修改)
输入数据库矩阵:xb = nb * d:32-bit floating point matrices, d = 64(特征向量的维度,可以修改)
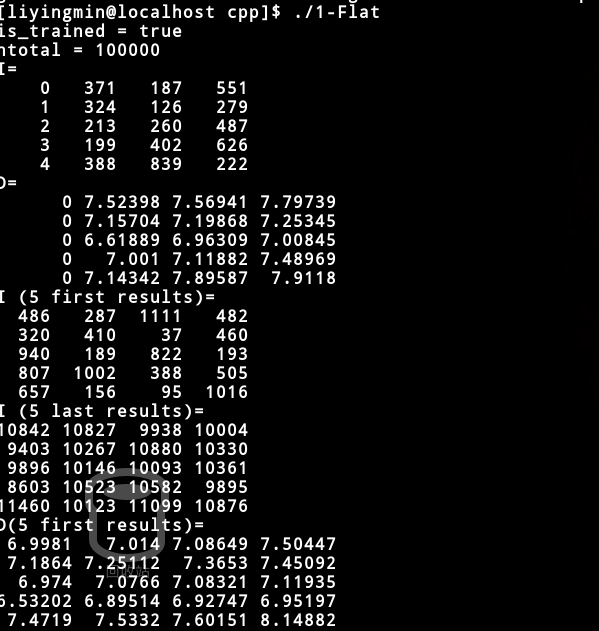
3.实际运算:
The output of the actual search is similar toID号:[[ 381 207 210 477][ 526 911 142 72][ 838 527 1290 425][ 196 184 164 359][ 526 377 120 425]]ID号:[[ 9900 10500 9309 9831][11055 10895 10812 11321][11353 11103 10164 9787][10571 10664 10632 9638][ 9628 9554 10036 9582]]Because of the value added to the first component of the vectors, the dataset is smeared along the first axis in d-dim space. So the neighbors of the first few vectors are around the beginning of the dataset, and the ones of the vectors around ~10000 are also around index 10000 in the dataset.
4.运行:
代码:
/*** Copyright (c) 2015-present, Facebook, Inc.* All rights reserved.** This source code is licensed under the BSD+Patents license found in the* LICENSE file in the root directory of this source tree.*/#include <cstdio>#include <cstdlib>#include <faiss/IndexFlat.h>int main() {int d = 64; // dimensionint nb = 100000; // database sizeint nq = 10000; // nb of queriesfloat *xb = new float[d * nb]; //database matrixfloat *xq = new float[d * nq]; //query matrixfor(int i = 0; i < nb; i++) {for(int j = 0; j < d; j++)xb[d * i + j] = drand48();xb[d * i] += i / 1000.; //just for fun!}for(int i = 0; i < nq; i++) {for(int j = 0; j < d; j++)xq[d * i + j] = drand48();xq[d * i] += i / 1000.;}faiss::IndexFlatL2 index(d); // call constructorprintf("is_trained = %s\n", index.is_trained ? "true" : "false"); //是否需要训练阶段index.add(nb, xb); // add vectors to the index,将database矩阵xb和database中特征向量的个数nb,给index对象printf("ntotal = %ld\n", index.ntotal); //返回database中特征向量的个数nbint k = 4; //KNN algorithm{ // sanity check: search 5 first vectors of xb,database矩阵xblong *I = new long[k * 5]; //记录ID 号float *D = new float[k * 5]; //记录实际距离index.search(5, xb, k, D, I); //第一个参数本来应该是nq,第二个参数本来应该是xq,表示在database matrix中查找与k个与xq batches最近的特征向量//现在相当于是在database矩阵中查找k个与xb自身5个batches最近的特征向量// print resultsprintf("I=\n");for(int i = 0; i < 5; i++) {for(int j = 0; j < k; j++)printf("%5ld ", I[i * k + j]);printf("\n");}printf("D=\n");for(int i = 0; i < 5; i++) {for(int j = 0; j < k; j++)printf("%7g ", D[i * k + j]);printf("\n");}delete [] I;delete [] D;}{ // search xqlong *I = new long[k * nq];float *D = new float[k * nq];index.search(nq, xq, k, D, I);// print resultsprintf("I (5 first results)=\n"); //只输出5行最开始的数据for(int i = 0; i < 5; i++) {for(int j = 0; j < k; j++)printf("%5ld ", I[i * k + j]);printf("\n");}printf("I (5 last results)=\n"); //只输出5个最后的数据for(int i = nq - 5; i < nq; i++) {for(int j = 0; j < k; j++)printf("%5ld ", I[i * k + j]);printf("\n");}printf("D(5 first results)=\n");for(int i = 0; i < 5; i++) {for(int j = 0; j < k; j++)printf("%7g ", D[i * k + j]);printf("\n");}delete [] I;delete [] D;}delete [] xb;delete [] xq;return 0;}
