Leetcode60. Permutation Sequence

ddddLeetcode刷题

• Author：李英民 | Henry
• E-mail: li_yingmin@outlookdotcom
• $Beijing~~U~of~Posts~and~Telecom$$(BUPT~)$
• Home: https://liyingmin.wixsite.com/henry

• 快速了解我: About Me

• 转载请保留上述引用内容，谢谢配合！

The set [1,2,3,…,n] contains a total of n! unique permutations.

By listing and labeling all of the permutations in order,

We get the following sequence (ie, for n = 3):

1. "123"
2. "132"
3. "213"
4. "231"
5. "312"
6. "321"

Given n and k, return the kth permutation sequence.

Note: Given n will be between 1 and 9 inclusive.

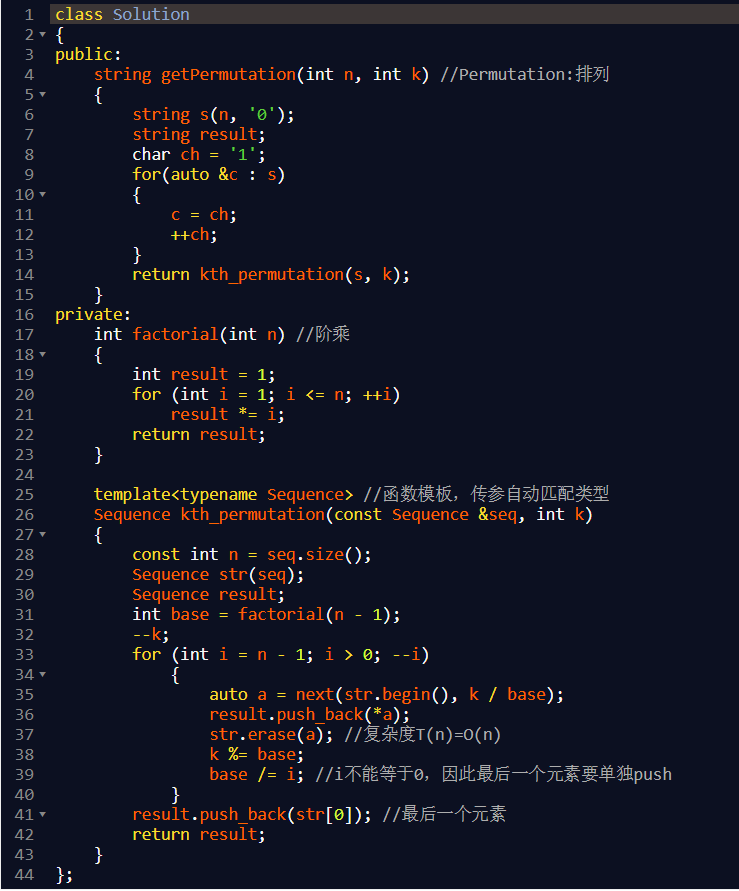
优秀代码：

//T(n)=O(n),S(n)=O(1)
class Solution
{
public:
    string getPermutation(int n, int k) //Permutation:排列
    {
        string s(n, '0');
        string result;
        char ch = '1';
        for(auto &c : s)
        {
            c = ch;
            ++ch;
        }
        return kth_permutation(s, k);
    }
private:
    int factorial(int n) //阶乘
    {
        int result = 1;
        for (int i = 1; i <= n; ++i)
            result *= i;
        return result;
    }
    template<typename Sequence> //函数模板，传参自动匹配类型
    Sequence kth_permutation(const Sequence &seq, int k)
    {
        const int n = seq.size();
        Sequence str(seq);
        Sequence result;
        int base = factorial(n - 1);
        --k; 
        for (int i = n - 1; i > 0; --i)
            {
                auto a = next(str.begin(), k / base);
                result.push_back(*a);
                str.erase(a); //复杂度T(n)=O(n)
                k %= base; 
                base /= i; //i不能等于0，因此最后一个元素要单独push
            }
        result.push_back(str[0]); //最后一个元素
        return result;
    }
};

•     char ch = '1';
      for(auto &c : s)
      {
          c = ch;
          ++ch;
      }
        //可以替换为：
      for (int i = 0; i < n; ++i)
          s[i] += i + 1;

• 康托编码

这样考虑：第一位是3，小于3的数有1、2 。所以有2*2!个。再看小于第二位，小于2的数只有一个就是1 ，所以有1*1!=1 所以小于32

的{1,2,3}排列数有2*2!+1*1!=5个。所以321是第6个大的数。2*2!+1*1!是康托展开。（注意判断排列是第几个时要在康托展开的结果后+1）

再举个例子：1324是{1,2,3,4}排列数中第几个大的数：第一位是1小于1的数没有，是0个，0*3!，第二位是3小于3的数有1和2，但1已经在第一位了，所以只有一个数2，1*2! 。第三位是2小于2的数是1，但1在第一位，所以有0个数，0*1!，所以比1324小的排列有0*3!+1*2!+0*1!=2个，1324是第三个大数。

又例如，排列3 5 7 4 1 2 9 6 8展开为98884，因为X=2*8!+3*7!+4*6!+2*5!+0*4!+0*3!+2*2!+0*1!+0*0!=98884.

解释：

排列的第一位是3，比3小的数有两个，以这样的数开始的排列有8!个，因此第一项为2*8!

排列的第二位是5，比5小的数有1、2、3、4，由于3已经出现，因此共有3个比5小的数，这样的排列有7!个，因此第二项为3*7!

以此类推，直至0*0!

三、全排列的解码
如何找出第16个（按字典序的）{1,2,3,4,5}的全排列？

1. 首先用16-1得到15

2. 用15去除4! 得到0余15

3. 用15去除3! 得到2余3

4. 用3去除2! 得到1余1

5. 用1去除1! 得到1余0

有0个数比它小的数是1，所以第一位是1

有2个数比它小的数是3，但1已经在之前出现过了所以是4

有1个数比它小的数是2，但1已经在之前出现过了所以是3

有1个数比它小的数是2，但1,3,4都出现过了所以是5

最后一个数只能是2

所以排列为1 4 3 5 2