离散数学作业08

离散数学作业

---

第8次作业

1、课本P251，习题14、15。
2、在各自的专业领域中，分别举出6例图的应用实例，给出它的集合表示以及矩阵表示；其中2例分别是结点权图和边权图，另外还有至少1例是多重图。
3、在各自的专业领域中，给出实际中的收缩图操作的实例和导出图的实例。
4、写出流程图、伪代码算法或编程实现，对从键盘输入的任意字符串，判定它是某个图的合法的集合表示。
5、本次作业同样在5月26日之前提交给我。

第八章 习题

第14题

证明:
因为$f$是从$A$到$A$的满射，所以对$\forall x \in A$，存在

$$f(a1)=a,f(f(a1))=f(a)=f(a1),f(a1)=a,f(a)=a$$
所以对$f=I_A$

第15题

证明：
若$f$是$A$到$B$的满射，$\forall b1,b2 \in B$,则存在$a1,a2 \in A$,使得$f(a1)=b1,f(a2)=b2$
且$f(a1) \neq f(a2)$,由于$f$是函数，所以$a1 \neq a2$
又有

$$g(b1)={x|(x \in A) \wedge (f(x)=b1) } , g(b2)={x|(x \in A) \wedge (f(x)=b2) }$$
所以$a1 \in g(b1),a2 \in g(b2)$,且$a1 \notin g(b2),a2 \notin g(b1)$。因此$g$是单射

六个图的实例

边权图

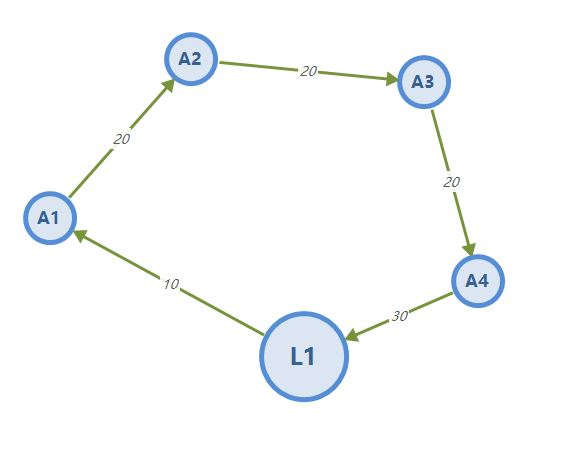
设有一条闭合水准路线L1、A1、A2、A3、A4、L1，边长分别为100m，200m,200m,200m,300m，其权均为边长除以总边长
集合表示$G=<V,E> V={ L1,A1,A2,A3,A4 }$
$E={<L1,A1>，<A1,A2>，<A2,A3>,<A3,A4>,<A4,L1>}$
矩阵表示

$$\begin{pmatrix} 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\\ 1 & 0 & 0 & 0 & 0 \end{pmatrix}$$

点权图

设一个地区有A1、A2、A3、A4四个县，每个县对当地GDP的贡献比例分别为25%、15%、20%、40%
集合表示$G=<V,E> ,V={ A1,A2,A3,A4 }$
$E={<A1,A2>，<A2,A3>,<A3,A4>,<A4,A1>}$
矩阵表示

$$\begin{pmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \end{pmatrix}$$

一个闭合路线的工程测量路线中，共有A,B,C,D四个测站，从A到B,B到C，C到D,D到A各有一条有向边连接，分别用e1,e2,e3,e4表示
集合表示$G={A,B,C,D},{<A,B><B,C><C,D>,<D,A>}$
矩阵表示

$$\begin{pmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0& 0 \end{pmatrix}$$

a,b,c,d,e分别代表五个地方，有边代表他们有路到达。e1=(a,b)e2=(a,c)e3=(a,d)e4=(a,e),e5=(b,c)e6=(b,e)e7=(c,d)e8=(c,e)e9=(d,e)
集合表示$G={a,b,c,d,e},{e1,e2,e3,e4,e5,e6,e7,e8,e9}$
矩阵表示

$$\begin{pmatrix} 0 & 1 & 1 & 1 & 1 \\ 1 & 0 & 1 & 0 & 1\\ 1 & 1 & 0 & 1 & 1\\ 1 & 0 & 1 & 0 & 1\\ 1 & 1 & 1 & 1 & 0 \end{pmatrix}$$

     0,1,1,1,1,
    1,0,1,0,1,
    1,1,0,1,1,
    1,0,1,0,1,
    1,1,1,1,0]