No.8

摘要：本次主要研究混沌现象。混沌是自然界普遍存在的现象。混沌现象是指发生在确定性系统中的貌似随机的不规则运动，一个确定性理论描述的系统，其行为却表现为不确定性一不可重复、不可预测，这就是混沌现象。进一步研究表明，混沌是非线性动力系统的固有特性，是非线性系统普遍存在的现象。牛顿确定性理论能够充分处理的多为线性系统，而线性系统大多是由非线性系统简化来的。因此，在现实生活和实际工程技术问题中，混沌是无处不在的。

背景

单摆在重力、外部驱动力、阻尼的作用下运动，其相应的方程为

$$\frac{d^2\theta}{dt^2}=-\frac{g}{l}sin(\theta)-q\frac{d\theta}{dt}+F_Dsin(\Omega_D t)$$
将二阶微分方程化为两个一阶微分方程以便使用欧拉法编程： $$\frac{d\omega}{dt}=-\frac{g}{l}sin(\theta)-q\frac{d\theta}{dt}+F_Dsin(\Omega_D t)$$ $$\frac{d\theta}{dt}=\omega$$
因此相应的运算为 $$\omega_{i+1}=\omega_i-[\frac{g}{l}sin\theta_i+q\omega_i+F_Dsin(\Omega_D t_i)]\Delta t$$ $$\theta_{i+1}=\theta_i+\omega_{i+1}\Delta t$$ $$t_{i+1}=t_i+\Delta t$$
另应注意$\theta_{i+1}$的取值是否在$[-\pi,\pi]$,如超出了范围应相应的加上$\pi$或减去$\pi$

正文(3.18)

• 取time_step=0.01 , initial_$\theta$1=0.2,$F_D$=1.2,g=9.8,l=9.8,q=0.5,$\Omega_D=2/3$

• 部分代码

  def run1(self):
      while self.t[-1]<=self.time:
          temp1=self.w1[-1]-self.g*self.dt*math.sin(self.theta1[-1])/self.l-self.q*self.dt*self.w1[-1]-self.Fd*self.dt*math.sin(self.omegaD*self.t[-1])
          self.w1.append(temp1)
          temd1=self.theta1[-1]+self.w1[-1]*self.dt
          self.theta1.append(temd1)
          if self.theta1[-1] < -math.pi:
              self.theta1[-1]=self.theta1[-1]+2*math.pi
          if self.theta1[-1] > math.pi:
              self.theta1[-1]=self.theta1[-1]-2*math.pi
          self.t.append(self.t[-1]+self.dt)
          phase=self.t[-1]-2*self.na[-1]*math.pi/self.omegaD
          if -0.005< phase <0.005:
              self.w.append(temp1)
              self.theta.append(temd1)
              self.na.append(self.na[-1]+self.n)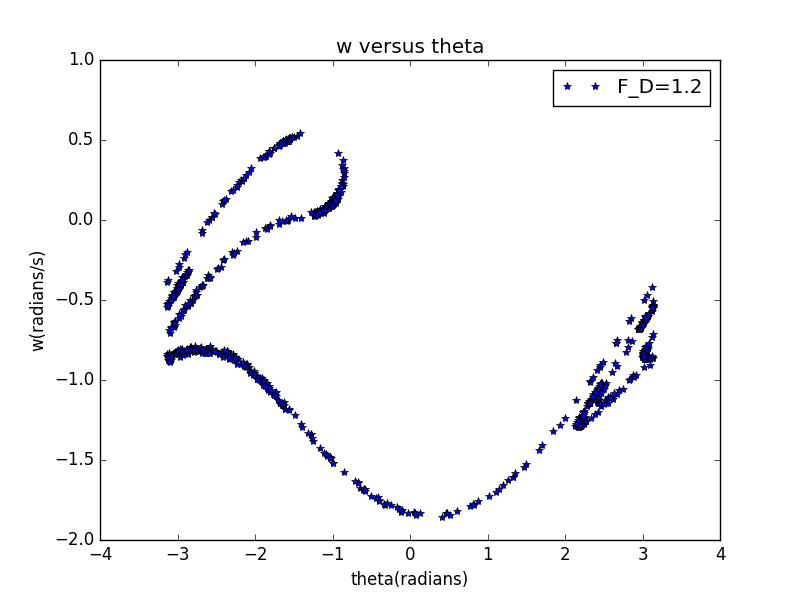
  

• 

• 这是F_D=1.2的图像

• 改变F_D=1.4、1.44、1.465

• 相应的绘图

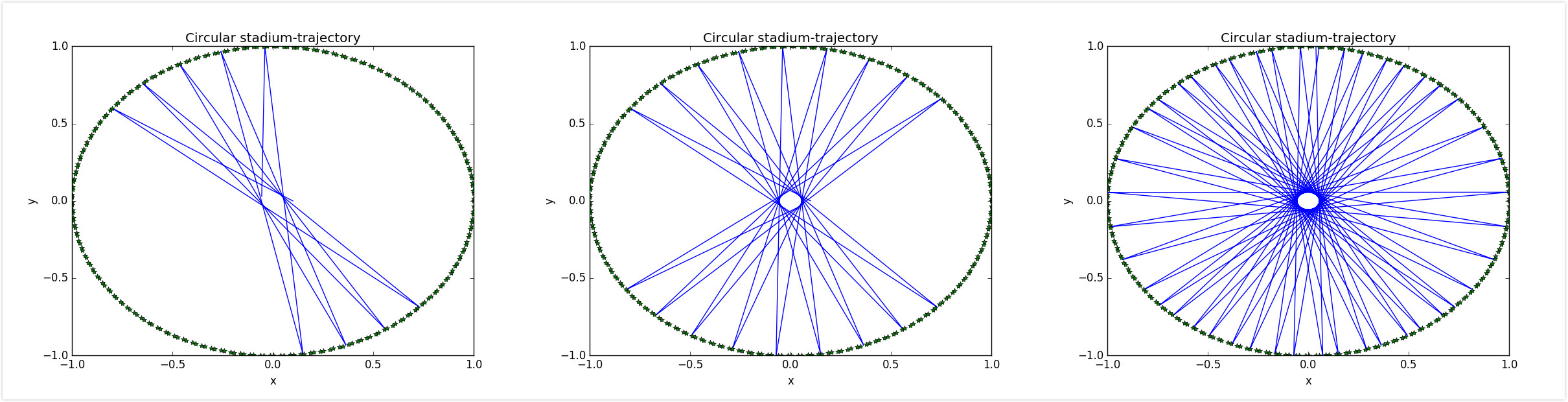
• 从图中可以看到F_D变化带来的图像变化，绘出的点不再分散。
  F_D=1.4时可看到一个聚点，F_D=1.44时可看到两个聚点，F_D=1.465时可看到四个聚点。
  由于程序的精度等问题还有少量几个点是分散的，并没有完全聚到一起

• Bifurcation diagram

• 
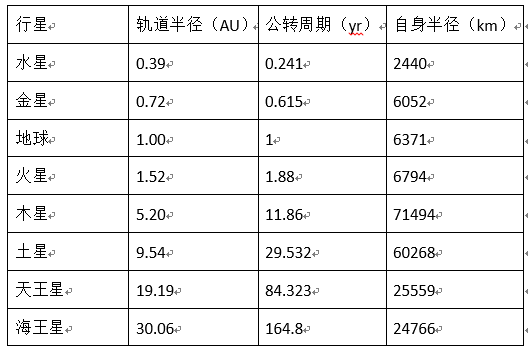
  程序还存在一些问题，有待改进。

结论

3.18 根据F_D的改变可以看出相应period的变化：1——>2——>4。

致谢

Bifurcation diagram的部分程序参考了江俊的代码