No.4

摘要

在处理物理问题时，经常会遇到微分方程。其中一阶常微分方程的初值问题数值解可由欧拉法求得。此次处理的问题是两种粒子由初始状态开始相互转化直至达到平衡，变换的过程将通过算法得以绘制成图，还将比较在不同初始值下曲线的变化及不同时间间隔下的曲线变化，再对程序进行检验。

背景介绍

欧拉法：铀的衰变方程为$\frac{dN_U}{dt}=-\frac{N_U}{\tau}$。$N_U(t)$的泰勒展开式为$N_U(\Delta t)=N_U(0)+\frac{dN_A}{dt}\Delta t+\frac{1}{2}\frac{d^2N_U}{dt^2}(\Delta t)^2+\ldots$
所以$N_U(t+\Delta t)\approx N_U(t)+\frac{dN_U}{dt}\Delta t$
又$\frac{dN_U}{dt}\approx\frac{N_U(t+\Delta t)-N_U(t)}{\Delta t}$
推得$N_U(t+\Delta t)\approx N_U(t)-\frac{N_U(t)}{\tau}\Delta t$ 已知$N_U(0)$,确定好$\tau,\Delta t$取值，即可通过此式进行编程运算求解。类似的问题亦可如此解决。
A、B粒子的‘衰变’问题：A粒子可以转化为B粒子，B粒子也可以转化为A粒子。相应的转换速率方程为$\frac{dN_A}{dt}=\frac{N_B}{\tau}-\frac{N_A}{\tau}$,$\frac{dN_B}{dt}=\frac{N_A}{\tau}-\frac{N_B}{\tau}$。改变$N_A$及$N_B$的初始取值，取$\tau$=1s,来验证系统会达到平衡状态，$N_A$及$N_B$为常数。

正文

• 取初始$N_A$=1000，$N_B$=0，$\tau$=1s，$\Delta t$=0.01s，总的时间为10s。

  import pylab as pl
  class two_types_nuclei_decay:
   """
   Simulation of a decay problem with two types of nuclei A and B
   """
      def __init__(self,  number_of_nucleiA = 1000, number_of_nucleiB =0, time_constant = 1, time_of_duration = 10, time_step = 0.01):
          self.na = [number_of_nucleiA]
          self.nb = [number_of_nucleiB]
          self.t = [0]
          self.tau = time_constant
          self.time = time_of_duration
          self.dt = time_step
          self.nsteps = int(time_of_duration // time_step + 1)
          print("Initial number of nuclei A ->", number_of_nucleiA)
          print("Initial number of nuclei B ->", number_of_nucleiB)
          print("Time constant ->", time_constant)
          print("time step -> ", time_step)
          print("total time -> ", time_of_duration)
      def calculate(self):
          for i in range(self.nsteps):
              tmp = self.na[i] - self.na[i] / self.tau * self.dt + self.nb[i] / self.tau * self.dt
              self.na.append(tmp)
              tmd = self.nb[i] - self.nb[i] / self.tau * self.dt + self.na[i] / self.tau * self.dt
              self.nb.append(tmd)
              self.t.append(self.t[i] + self.dt)
      def show_results(self):
          pl.plot(self.t,self.na,color='red',linewidth=2.0,linestyle='-',label='the element A')
          pl.plot(self.t,self.nb,color='blue',linewidth=2.0,linestyle='-',label='the element B')
          pl.legend(loc='upper right',frameon=True)
          pl.title('the radioactive decay line')
          pl.xlabel('time/s')
          pl.ylabel('number of nuclei')
          pl.plot([0,10],[500,500],linewidth=1.0,linestyle='--')
          pl.annotate(r'$(500.0)$',
              xy=(8,500.0),xycoords='data',
              xytext=(+10,+30),textcoords='offset points',fontsize=16,
              arrowprops=dict(arrowstyle="->",connectionstyle="arc3,rad=.2"))
          pl.show()
  
  
   b = two_types_nuclei_decay(number_of_nucleiA=1000, time_constant=1)
   b.calculate()
   b.show_results()
   c = two_types_nuclei_decay(number_of_nucleiB=0,     time_constant=1)
   c.calculate()
   c.show_results()
  

• 绘得相应图像

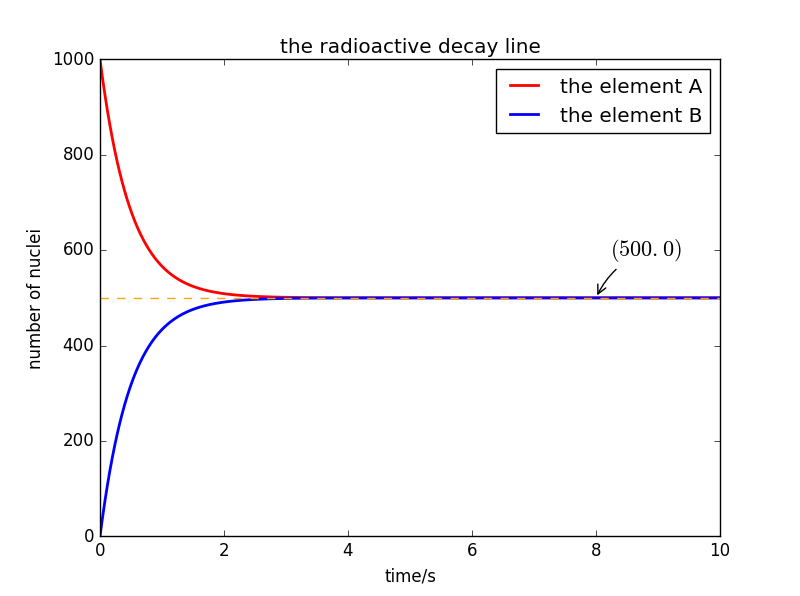
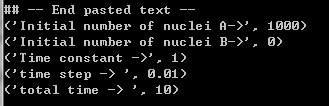
• 程序运行后的显示数值
• 改变相应的取值后 取初始$N_A$=400，$N_B$=600，$\tau$=1s，$\Delta t$=0.01s，总的时间为10s。
• 绘得相应图像
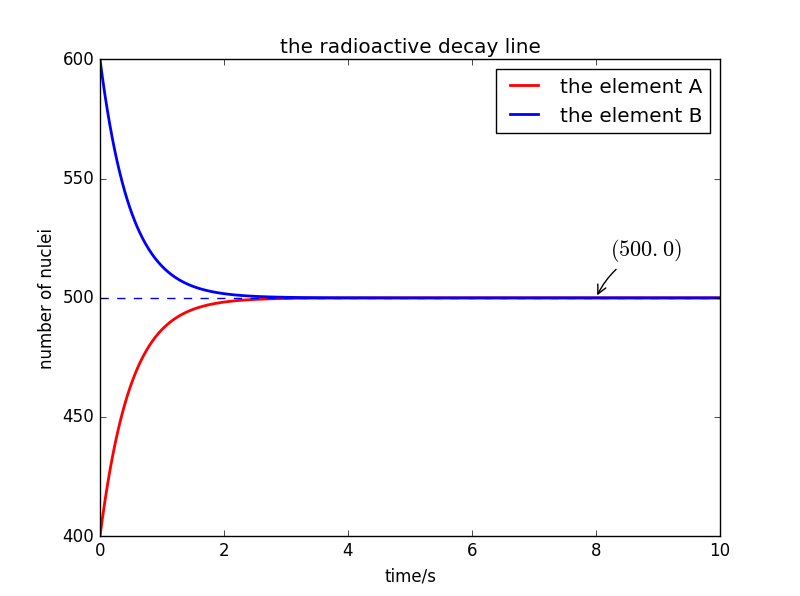
• 程序运行后的显示数值
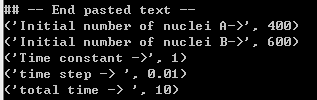
• 取初始$N_A$=400，$N_B$=600，$\tau$=2s，$\Delta t$=0.01s，总的时间为10s
• 绘得相应图像
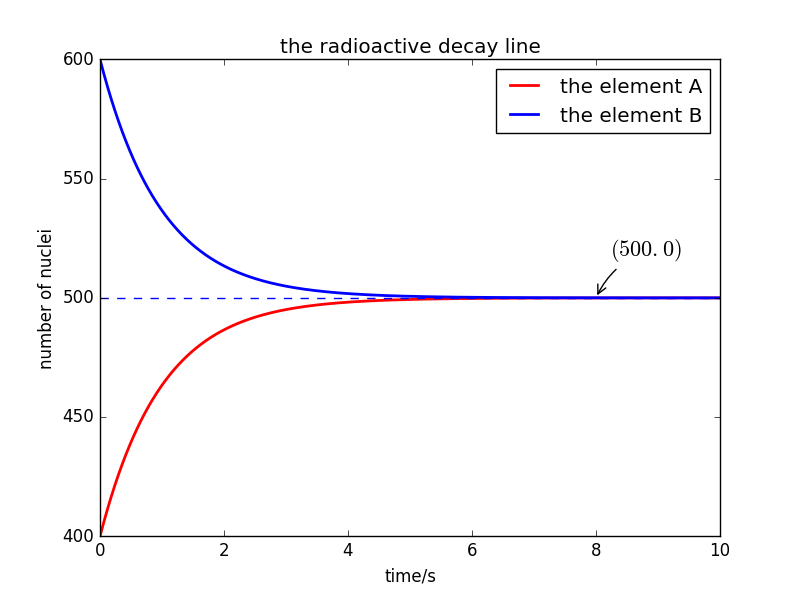
• 对程序测试：
  由所给出的方程$\frac{dN_A}{dt}=\frac{N_B}{\tau}-\frac{N_A}{\tau}$,$\frac{dN_B}{dt}=\frac{N_A}{\tau}-\frac{N_B}{\tau}$，可解得
  $N_A=\frac{N}{2}+(N_A(0)-\frac{N}{2})e^\frac{-2t}{\tau}$
  $N_B=\frac{N}{2}-(N_A(0)-\frac{N}{2})e^\frac{-2t}{\tau}$
  N为粒子总数

• 相应的程序（直接添加在原程序后）

  from math import *
  class exact_results_check(two_types_nuclei_decay):
      def show_results(self):
          self.ea = []
          self.eb = [] 
          for i in range(len(self.t)):
              tema = (self.na[0]+self.nb[0])*0.5 + (self.na[0]-self.nb[0]) * exp(-2* self.t[i] / self.tau)*0.5
              temb = (self.na[0]+self.nb[0])*0.5 - (self.na[0]-self.nb[0]) * exp(-2* self.t[i] / self.tau)*0.5
              self.ea.append(tema)
              self.eb.append(temb)
          pl.plot(self.t, self.ea, '*', label='LineA')
          pl.plot(self.t, self.eb, '+', label='LineB')
          pl.plot(self.t,self.na,color='red',linewidth=2.0,linestyle='-',label='the element A')
          pl.plot(self.t,self.nb,color='blue',linewidth=2.0,linestyle='-',label='the element B')
          pl.legend(loc='upper right',frameon=True)
          pl.xlabel('time ($s$)')
          pl.ylabel('Number of Nuclei')
          pl.title('the radioactive decay line')
          pl.xlim(0, self.time)
          pl.show()
  
  d = exact_results_check(number_of_nucleiA=1000,number_of_nucleiB=0, time_constant=1, time_step=0.1)
  d.calculate()
  d.show_results()     
  

• 绘得图片

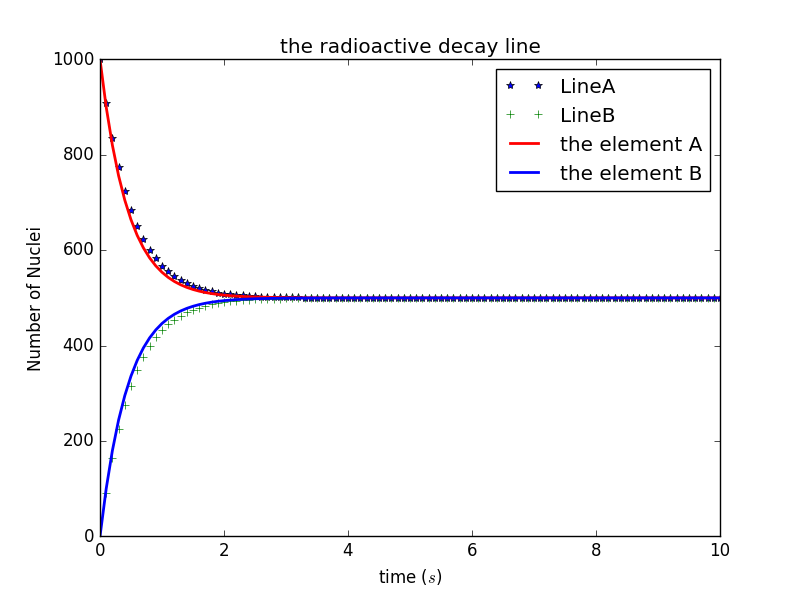
• 最后改变step size，看结果是否一致

• 相应程序

  class diff_step_check(two_types_nuclei_decay):
      def show_results(self, style = 'b'):
          pl.plot(self.t, self.na, style)
          pl.plot(self.t, self.nb, style)
          pl.title('the radioactive decay line') 
          pl.xlabel('time ($s$)')
          pl.ylabel('Number of Nuclei')
          pl.xlim(0, self.time)
  from pylab import *
  b = diff_step_check(number_of_nucleiA=1000,number_of_nucleiB =0,    time_constant=1, time_step=0.25)
  b.calculate()
  b.show_results('b')
  c = diff_step_check(number_of_nucleiA=1000,number_of_nucleiB =0, time_constant=1, time_step=0.01)
  c.calculate()
  c.show_results('r')
  show()
  

• 运行结果图
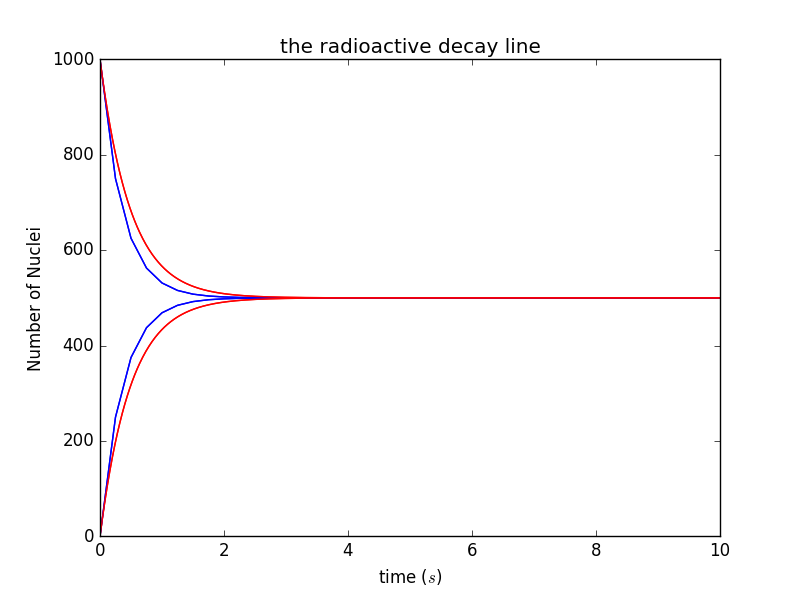
  红线：stepsize=0.01，蓝线：stepsize=0.25
  step改变后，曲线的大致走向和结果不变，细节部分数值有所改变。

结论

由上面的运行结果可知系统经过弛豫时间后达到平衡，$N_A$及$N_B$保持为常数。通过校验及step的改变，可以看出欧拉法能够较好的拟合实际的曲线，当step越小绘出的曲线越接近实际曲线。

致谢

• 老师提供的完整编码
• 13级强雨学长绘图部分的编码