No.5

摘要：用不同的空气密度模型来计算加农炮的炮弹运动轨迹。也可将B2的值和温度联系起来获得不同的曲线。观察adiabatic模型对射程的影响，温度对于曲线的影响

背景

炮弹在空中飞行受到重力与空气阻力的影响

$$\frac{d^2x}{dt^2}=0$$ $$\frac{d^2y}{dt^2}=-g$$ $$F_{drag,x}=-B_2vv_x$$ $$F_{drag,y}=-B_2vv_y$$
通过这几个式子可解得： $x_{i+1}=x_i+v_{x,i}\Delta t$
$v_{x,i+1}=v_{x,i}-\frac{B_2vv_{x,i}}{m}\Delta t$
$y_{i+1}=y_i+v_{y,i}\Delta t$
$v_{y,i+1}=v_{y,i}-\frac{B_2vv_{y,i}}{m}\Delta t-g\Delta t$
又空气密度会随高度改变，有两个模型
（1）$p(y)=p(0)e^{-\frac{mgy}{k_BT}}$
$\rho=\rho_0exp(-y/y_0)$
(2)$\rho=\rho_0(1-\frac{ay}{T_0})^\alpha$
根据两个模型，有$F_{drag}^*=\frac{\rho}{\rho_0}F_{drag}(y=0)$
将$F_{drag}^*$以上公式，即可进行编辑代码。

正文

• 采用第二个模型进行编码 取time_step=0.01 ,angle=1, initial_v=700, T0=273

• 代码

  import math
  import pylab as pl
  class cannon_shell1:
      def __init__(self, time_step=0.01 ,angle=1, initial_v=700, T0=273, b=0.0065, Bm=0.00004,g=9.8,c=2.5,y0=10000):
          self.y = [0]
          self.x = [0]
          self.t = [0]
          self.ang = angle
          self.v = [initial_v]
          self.vx =[initial_v*math.cos(self.ang)]
          self.vy =[initial_v*math.sin(self.ang)]
          self.b = b
          self.Bm = Bm
          self.T0 = T0
          self.dt = time_step
          self.g=g
          self.c=c
          self.y0 = y0
      def run1(self):
          _time=0
          while (self.y[-1]>=0):
              self.vx.append(self.vx[-1]-self.Bm*self.dt*self.v[-1]*self.vx[-1]*(1-self.b*self.y[-1]/self.T0)**self.c)
              self.vy.append(self.vy[-1]-self.g*self.dt-self.Bm*self.dt*self.v[-1]*self.vy[-1]*(1-self.b*self.y[-1]/self.T0)**self.c)
              self.y.append(self.y[-1]+self.vy[-1]*self.dt)
              self.x.append(self.x[-1]+self.vx[-1]*self.dt)
              self.v.append(math.sqrt(self.vx[-1]*self.vx[-1]+self.vy[-1]*self.vy[-1]))
              self.t.append(_time)
              _time+=self.dt
      def show_results(self):
          font = {'family': 'serif','color': 'darkred','weight': 'normal','size': 16,}
          pl.plot(self.x, self.y)
          pl.title('cannon shell trajectories with air drag', fontdict = font)
          pl.xlabel('x/m')
          pl.ylabel('y/m')
          pl.ylim(0,12000)    
  a = cannon_shell1()
  a.run1()
  a.show_results()
  pl.show()
  

• 相应图像
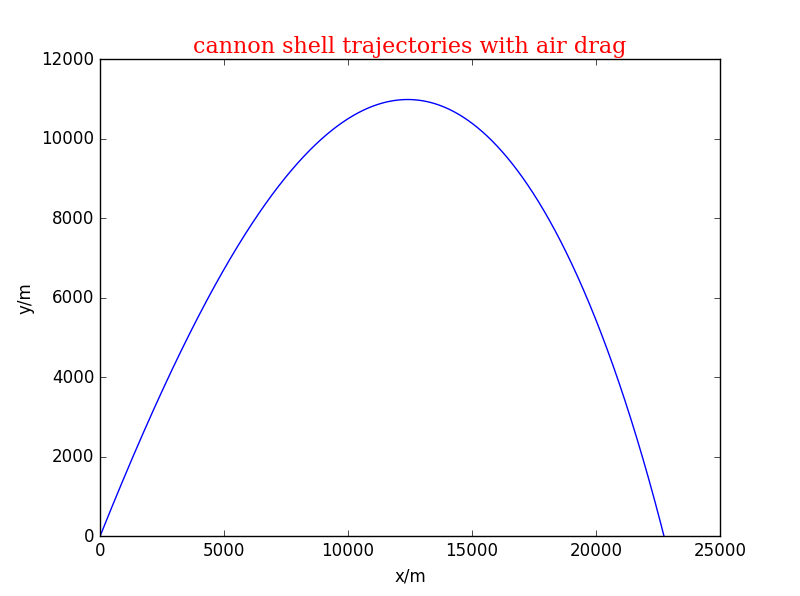
• 同时考虑两个模型 在原程序后去掉输出项，重新加上新的定义函数，最后总输出。初始值不变。

• 代码

  class cannon_shell2:
      def __init__(self, time_step=0.01 ,angle=1, initial_v=700, T0=273, b=0.0065, Bm=0.00004,g=9.8,c=2.5,y0=10000):
          self.y = [0]
          self.x = [0]
          self.t = [0]
          self.ang = angle
          self.v = [initial_v]
          self.vx =[initial_v*math.cos(self.ang)]
          self.vy =[initial_v*math.sin(self.ang)]
          self.b = b
          self.Bm = Bm
          self.T0 = T0
          self.dt = time_step
          self.g=g
          self.c=c
          self.y0 = y0
      def run2(self):
          _time=0
          while (self.y[-1]>=0):
              self.vx.append(self.vx[-1]-self.Bm*self.dt*self.v[-1]*self.vx[-1]*math.exp(-self.y[-1]/self.y0))
              self.vy.append(self.vy[-1]-self.g*self.dt-self.Bm*self.dt*self.v[-1]*self.vy[-1]*math.exp(-self.y[-1]/self.y0))
              self.y.append(self.y[-1]+self.vy[-1]*self.dt)
              self.x.append(self.x[-1]+self.vx[-1]*self.dt)
              self.v.append(math.sqrt(self.vx[-1]*self.vx[-1]+self.vy[-1]*self.vy[-1]))
              self.t.append(_time)
              _time+=self.dt
      def show_results(self):
          font = {'family': 'serif','color': 'darkred','weight': 'normal','size': 16,}
          pl.plot(self.x, self.y)
          pl.title('cannon shell trajectories with air drag', fontdict = font)
          pl.xlabel('x/m')
          pl.ylabel('y/m')
          pl.ylim(0,12000)
  a = cannon_shell1()
  a.run1()
  a.show_results()
  b = cannon_shell2()
  b.run2()
  b.show_results()
  pl.show()
  

• 图像
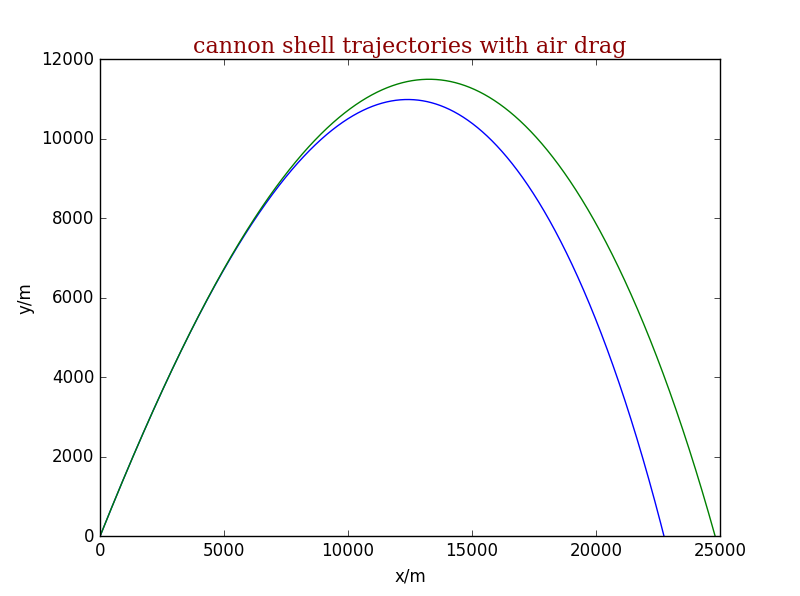
  绿色为模型一，蓝色为模型二，可看出两者的差距还是很大的。
• 用$B_2^{ref}(T_0/T_{ref})^{\alpha}$代替$B_2$ 取T=300K T0=273K

• 代码

  class cannon_shell3:
      def __init__(self, time_step=0.01 ,angle=1, initial_v=700, T0=273, b=0.0065, Bm=0.00004,g=9.8,c=2.5,y0=10000,T=300):
          self.y = [0]
          self.x = [0]
          self.t = [0]
          self.ang = angle
          self.v = [initial_v]
          self.vx =[initial_v*math.cos(self.ang)]
          self.vy =[initial_v*math.sin(self.ang)]
          self.b = b
          self.Bm = Bm
          self.T0 = T0
          self.T = T
          self.dt = time_step
          self.g=g
          self.c=c
          self.y0 = y0
      def run3(self):
          _time=0
          while (self.y[-1]>=0):
              self.vx.append(self.vx[-1]-(self.Bm*(self.T0/self.T)**self.c)*self.dt*self.v[-1]*self.vx[-1]*(1-self.b*self.y[-1]/self.T0)**self.c)
              self.vy.append(self.vy[-1]-self.g*self.dt-(self.Bm*(self.T0/self.T)**self.c)*self.dt*self.v[-1]*self.vy[-1]*(1-self.b*self.y[-1]/self.T0)**self.c)
              self.y.append(self.y[-1]+self.vy[-1]*self.dt)
              self.x.append(self.x[-1]+self.vx[-1]*self.dt)
              self.v.append(math.sqrt(self.vx[-1]*self.vx[-1]+self.vy[-1]*self.vy[-1]))
              self.t.append(_time)
              _time+=self.dt
      def show_results(self):
          font = {'family': 'serif','color': 'red','weight': 'normal','size': 16,}
          pl.plot(self.x, self.y)
          pl.title('cannon shell trajectories with air drag', fontdict = font)
          pl.xlabel('x/m')
          pl.ylabel('y/m')
          pl.ylim(0,20000)
  a = cannon_shell1()
  a.run1()
  a.show_results()
  b = cannon_shell3()
  b.run3()
  b.show_results()
  pl.show()
  

• 图片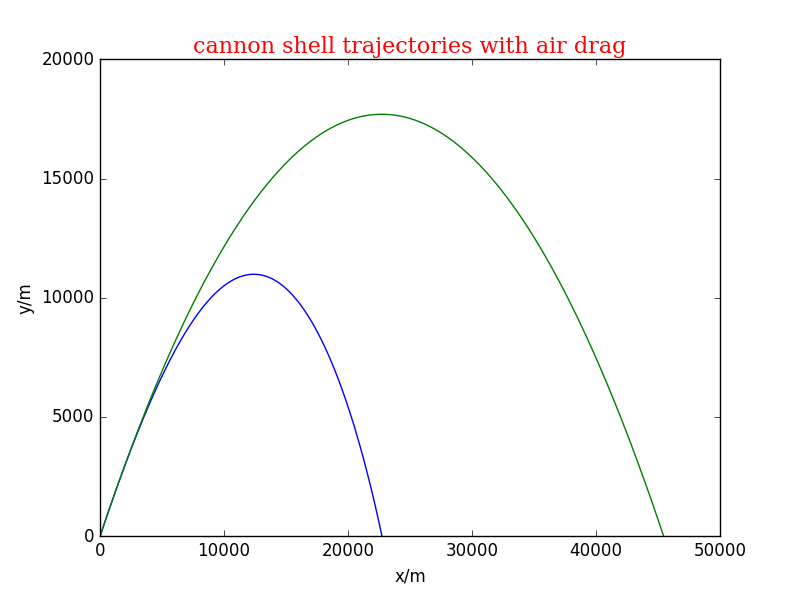绿色为改变B2后
  图像的变化很大，程序应该存在问题，改变T0=299.1 得到图像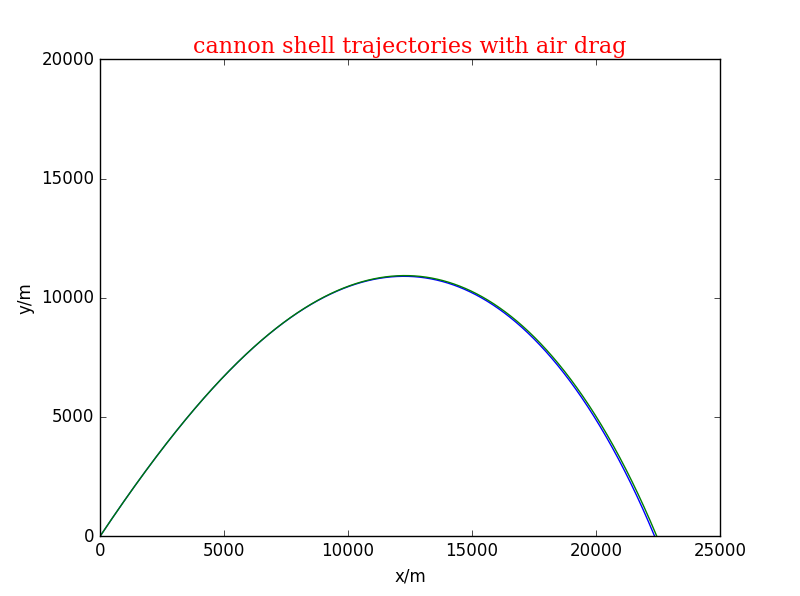
  此时图像变化不大，T0改变了0.1，可能数据的取值存在问题。
• 对于模型（2），改变初始速度角度，观察量程的变化。angle依次为0.5、0.6、0.7、0.8、0.9、1弧度
• 
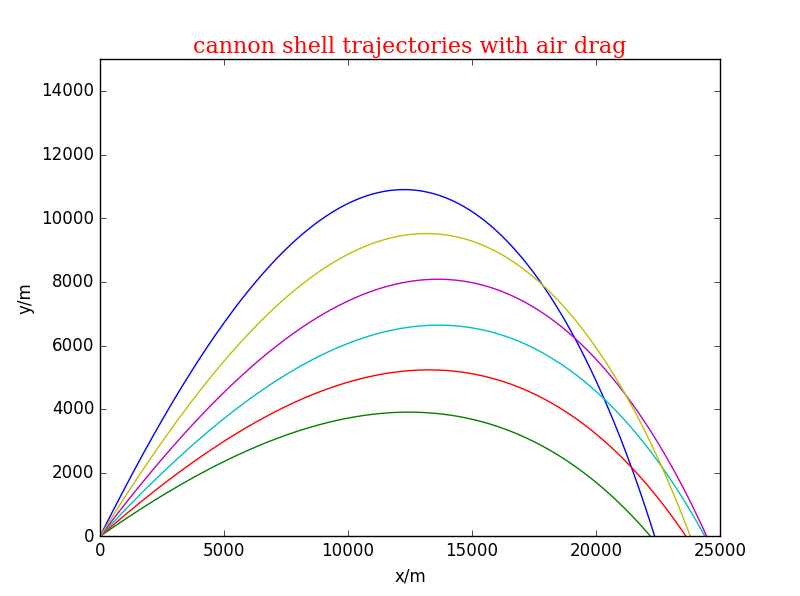
  由图像可以看出在0.7~0.8之间取值可以达到最大量程
• 对于模型（1），改变初始速度角度，观察量程的变化。angle依次为0.5、0.6、0.7、0.8、0.9、1弧度
• 
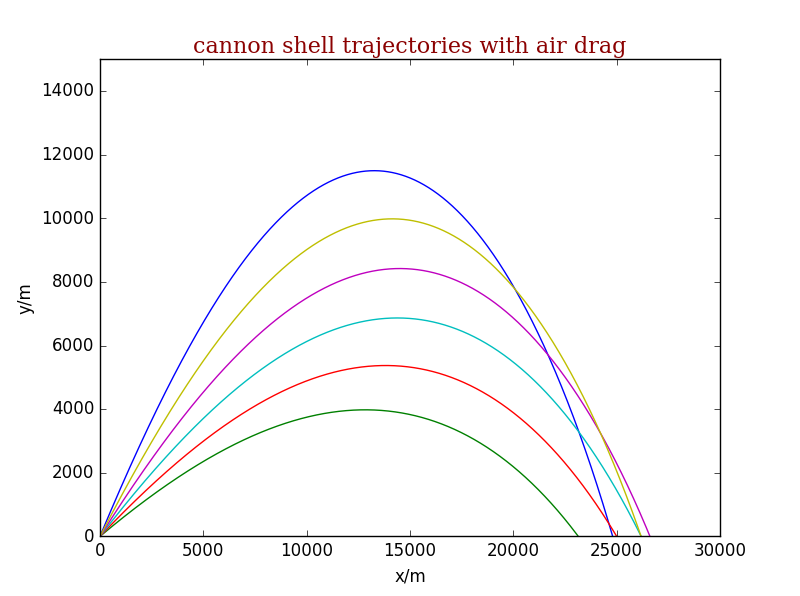
  由图像可以看出在0.7~0.8之间取值可以达到最大量程
• 与温度相关的曲线因为程序有些问题所以没有绘出。

结论

密度模型，温度，发射角度对轨迹的影响都很大。将两模型的轨迹进行比较，可知模型二的射程较小，模型一能达到更远的距离。当发射角度在0.7~0.8弧度之间时，射程最大。

致谢

老师提供的部分代码