函数的递归--m个苹果放进n个盘子

计算机

题目描述

• 把M个相同的苹果放在N个同样的盘子里，允许有的盘子空着不放，问共有多少种不同的分法？
• 注意：5，1，1和1，5，1是同一种分法
• 输入：7 3
• 输出：8

问题：M个苹果放入N个盘子，有多少种分法？

解题思路

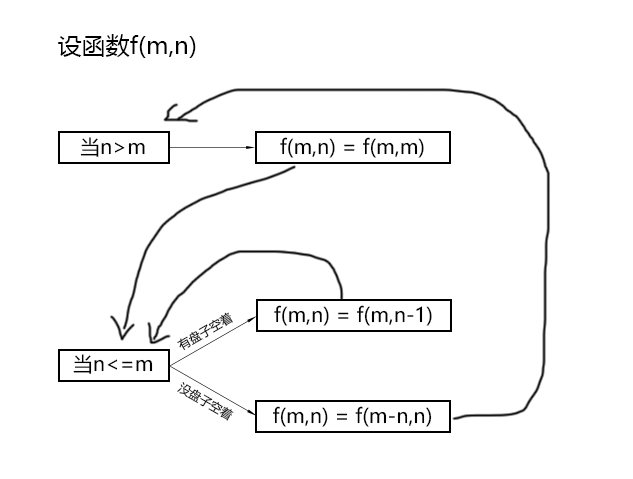
假设存在一个函数能算出当我们m个苹果放到n个盘子里的时候，有多少中解决方案。分析一下这样一个函数是如何进行运算的。

对于这道题目，分情况讨论：

1、 当n/盘子数 > m/苹果数

由于盘子数大于苹果数，这意味着就算每个盘子只放一个苹果，总会有(m-n)个盘子是空着的，这(m-n)个盘子对于苹果的放置方法不会产生任何影响。所以可以把多余的盘子拿掉。因此有：

if(n>m){
    f(m,n) = f(m,m);
}

2、当n/盘子数 < m/苹果数

根据题意，允许有的盘子空着不放。根据这个条件，把所有的放置方法分成两大类：

① 有盘子空着
② 没盘子空着

所有可能存在的放置方法的数目就等于分别在这两种情况下出现的放置方法数目的加和。
对以上两种情况再进行分析：

① 有盘子空着

在这个条件下，总是至少有一个盘子是空着的，而这一个空着的盘子对苹果的放置方法不会产生任何影响，这与条件1一样，可以把这个多余的盘子拿掉。因此有：

if(n <= m){
    f(m,n) = f(m,n-1);   //有盘子空着的情况
}

② 没盘子空着

在这种条件下，每个盘子都至少放有一个苹果。由于每个盘子里至少放着的那只苹果对于放置方法不会产生任何影响，因此我们又可以把每个盘子里那只多余的苹果拿掉。因此有：

if(n <= m){
    f(m,n) = f(m-n,n);   //没盘子空着的情况
}

这时，当每个盘子欧度拿掉一只苹果只有，我们又回到了条件1讨论的那种情况，即盘子数大于苹果数。因此又可以拿掉多余的盘子。

在拿掉多余的盘子的基础上，我们又回到了条件2所讨论的那种情况，即盘子数等于苹果数。在这种情况下，放置方法又可以分为①有盘子空着和②没盘子空着两类。所以按照这种思路，可以一直分析下去。

到最后，只剩下一个盘子或者一个苹果，这时分析就结束了。

按照这种规律，我们已经把所有可能出现的情况全部都进行了分类，而我们需要得到的结果，就是把所有这些情况下的结果进行加和。

用C语言表述为：

#include<stido.h>
int count(int m,int n);
int main(){
    int apples;
    int plates;
    scanf("%d %d",&apples,plates);
    printf("%d",count(apples,plates));
    return 0;
}
int count(int m, int n){   // m为苹果数，n为盘子数
    if(m <= 1 || n <= 0)
        return 0;
    if(m<n)
        return count(m,m);
    else
        return count(m,n-1)+count(m-n,n);
}

可以发现，虽然在分析过程中，解题思路比较复杂，但在程序语言中少量简短的语句便可以描述出来。

总结

为什么可以用这么简短的程序分析清楚这么多种情况呢？在这种场景中，递归帮我们进行自动分析。
运用递归设计程序的时候，其方法在于：

1. 先假设有一个函数fun()能够给出我们所需要答案，把关注点放在要求解的目标上（连续发生的动作是什么）；
2. 利用这个函数fun()的前提下， 分析如何解决问题，利用fun()来表示fun()，找出第n次执行与第n-1次执行之间的关系（不同次动作之间的关系）；
3. 弄清楚在最简单的情况下，其答案是什么，确定第1次的返回结果（边界条件是什么）。