第九次作业

homework

4.16 Carry out a true three-body simulation in which t he motions Of Earth, Jupiter, and the Sun are all calculated. Since all t h ree bodies are now in mo t ion ， it is useful to take the center Of mass Of t he three-body system the origin, rather than the position Of Sun. We also suggest that you give S u n an initial velocity which makes the total momentum Of the system exactly zero （So that the center of mass will remain fixed） ，study the motion Of Earth with different initial conditions. Also, try increasing the mass Of Jupiter to 10 ， 100 ， and 1000 times its true mass.

摘要

研究太阳、地球和木星三体的运动情况，采取三体的质心系作为坐标系，初始时刻给太阳一个初速度，使总的角动量为0，然后研究改变木星质量为原来的10,100,1000等倍数时对地球的运动情况。
木星对地球的引力为
$F_E,_J=GM_JM_E/r^2_E,_J$
在x方向上为
$F_E,_J，_x=-GM_JM_E(x_E-x_J)/r^3_E,_J$
取太阳的X.Y坐标均为0
则三体运动中地球的在X方向的引力为
$F_E,_J，_S,_x=-GM_JM_E(x_E-x_J)/r^3_E,_J-GM_SM_Ex_E/r^3_E,_S$
同理y方向的引力为
$F_E,_J，_S,_y=-GM_JM_E(y_E-y_J)/r^3_E,_J-GM_SM_Ey_E/r^3_E,_S$
这里$r_E,_J=((x_J-x_E）^2+(y_J-y_E)^2)^{1/2}$
$r_E,_S=(x_E^2+y_E^2)^{1/2}$
一倍木星质量时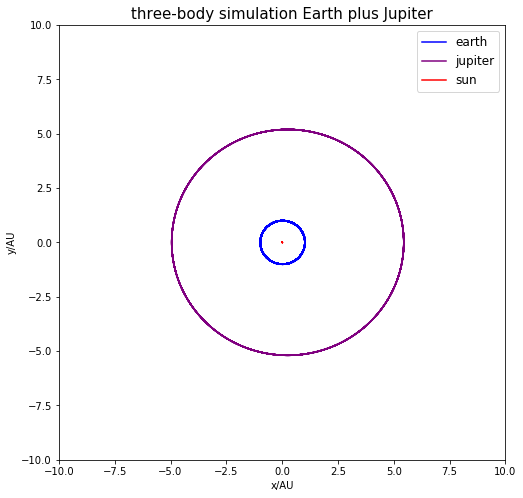
十倍木星质量时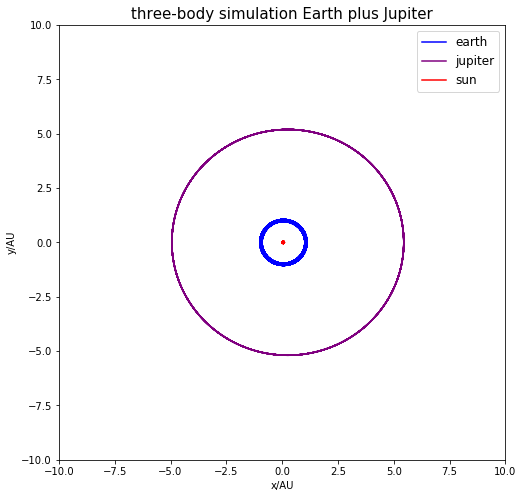
100倍木星质量时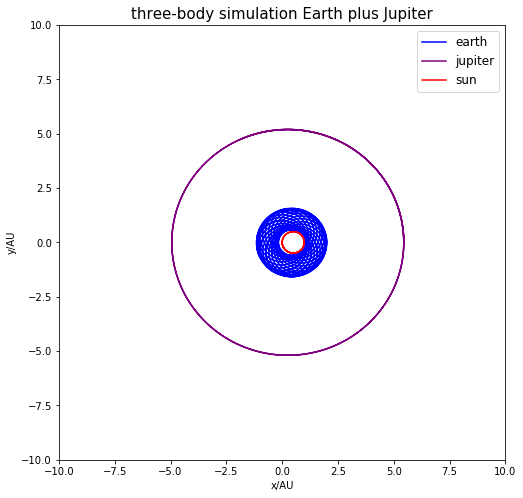
1000倍木星质量时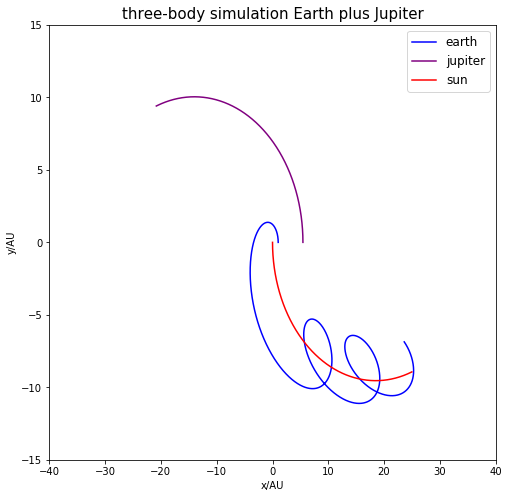
代码

import numpy as np
from pylab import *
import math
import matplotlib.pyplot as plt
#Determine the initial value
def initial(a,e):
    x0=a*(1+e)
v_y0=2*pi*sqrt((1-e)/(a*(1+e)))
return [x0,v_y0]
def three_orbits(m_e,m_j,m_s):
#Earth
x_e0=initial(1,0.017)[0]
x_e=[]
x_e.append(x_e0)

v_ex0=0
v_ex=[]
v_ex.append(v_ex0)

y_e0=0
y_e=[]
y_e.append(y_e0)

v_ey0=initial(1,0.017)[1]
v_ey=[]
v_ey.append(v_ey0)
#Jupiter
x_j0=initial(5.2,0.048)[0]
x_j=[]
x_j.append(x_j0)

v_jx0=0
v_jx=[]
v_jx.append(v_jx0)

y_j0=0
y_j=[]
y_j.append(y_j0)

v_jy0=initial(5.2,0.048)[1]
v_jy=[]
v_jy.append(v_jy0)
#Sun
x_s0=0
x_s=[]
x_s.append(x_s0)

v_sx0=0
v_sx=[]
v_sx.append(v_sx0)

y_s0=0
y_s=[]
y_s.append(y_s0)

v_sy0=-(m_e*v_ey0+m_j*v_jy0)/m_s
v_sy=[]
v_sy.append(v_sy0)
r_es=[]
r_es.append(math.sqrt((x_e0-x_s0)**2+(y_e0-y_s0)**2))
r_js=[]
r_js.append(math.sqrt((x_j0-x_s0)**2+(y_j0-y_s0)**2))
r_ej=[]
r_ej.append(math.sqrt((x_e0-x_j0)**2+(y_e0-y_j0)**2))

t=[]
t.append(0)
time=30.0
dt=0.001


for i in range(int(time/dt)):
#Earth
    v_ex.append(v_ex[i]+dt*(4*math.pi**2*(x_s[i]-x_e[i])/(r_es[i]**3)+4*math.pi**2*m_j/m_s*(x_j[i]-x_e[i])/(r_ej[i]**3)))
    x_e.append(x_e[i]+v_ex[i+1]*dt)
    v_ey.append(v_ey[i]+dt*(4*math.pi**2*(y_s[i]-y_e[i])/(r_es[i]**3)+4*math.pi**2*m_j/m_s*(y_j[i]-y_e[i])/(r_ej[i]**3)))
    y_e.append(y_e[i]+v_ey[i+1]*dt)
#Jupiter
    v_jx.append(v_jx[i]+dt*(4*math.pi**2*(x_s[i]-x_j[i])/(r_js[i]**3)+4*math.pi**2*m_e/m_s*(x_e[i]-x_j[i])/(r_ej[i]**3)))
    x_j.append(x_j[i]+v_jx[i+1]*dt)
    v_jy.append(v_jy[i]+dt*(4*math.pi**2*(y_s[i]-y_j[i])/(r_js[i]**3)+4*math.pi**2*m_e/m_s*(y_e[i]-y_j[i])/(r_ej[i]**3)))
    y_j.append(y_j[i]+v_jy[i+1]*dt)
#Sun
    v_sx.append(v_sx[i]+dt*(4*math.pi**2*m_e/m_s*(x_e[i]-x_s[i])/(r_es[i]**3)+4*math.pi**2*m_j/m_s*(x_j[i]-x_s[i])/(r_js[i]**3)))
    x_s.append(x_s[i]+v_sx[i+1]*dt)
    v_sy.append(v_sy[i]+dt*(4*math.pi**2*m_e/m_s*(y_e[i]-y_s[i])/(r_es[i]**3)+4*math.pi**2*m_j/m_s*(y_j[i]-y_s[i])/(r_js[i]**3)))
    y_s.append(y_s[i]+v_sy[i+1]*dt)

    r_es.append(math.sqrt((x_e[i+1]-x_s[i+1])**2+(y_e[i+1]-y_s[i+1])**2))
    r_js.append(math.sqrt((x_j[i+1]-x_s[i+1])**2+(y_j[i+1]-y_s[i+1])**2))
    r_ej.append(math.sqrt((x_e[i+1]-x_j[i+1])**2+(y_e[i+1]-y_j[i+1])**2))

    t.append(t[i]+dt)
return [x_e,y_e,x_j,y_j,x_s,y_s,t]
m_e=1.0
m_j=316.7*1000
m_s=333333.3
thr=three_orbits(m_e,m_j,m_s)
x_e=thr[0]
y_e=thr[1]
x_j=thr[2]
y_j=thr[3]
x_s=thr[4]
y_s=thr[5]
t=thr[6]

#plot
figure(figsize=[8,8])
plot(x_e,y_e,color='blue',label='earth')
plot(x_j,y_j,color='purple',label='jupiter')
plot(x_s,y_s,color='red',label='sun')
legend(('Earth','Jupiter','Sun'),'upper left')
title('three-body simulation Earth plus Jupiter',fontsize=15)
plt.xlabel('x/AU')
plt.xlim(-40,40)
plt.ylabel('y/AU')
plt.ylim(-15,15)
savefig('three-body trajectory.png')
legend(fontsize=12)
show()
#3D plot
fig = figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot(x_e,y_e,t,color='blue')
ax.plot(x_j,y_j,t,color='purple')
ax.plot(x_s,y_s,t,color='red')
ax.legend(('Earth','Jupiter','Sun'),'upper left')
ax.set_xlabel('x/Au')
ax.set_ylabel('y/AU')
ax.set_zlabel('t/yr')
savefig('three-body trajectory 3D.png')
show()

本代码借鉴了丁冬冬学姐的代码在此感谢