@rhj
2017-10-20T23:33:34.000000Z
字数 4397
阅读 150
2.20 knucklball
homework
--- 2.20. Calculate the effect of the knuckleball force on a batted ball.Assume that the ball is a line drive hit at an initial speed of the 90 mph and an angle of 20° and that the ball dose not spin at all(clearly a gross assumption).Let the rough side of the ball always face one side,which is perpendicular to the direction the ball is hit,and use Figure2.11 to estimate the magnitude of the lateral force.With all of these assumptions,calculate the lateral deflection of the ball.Such ball hits with very little spin are observed by outfielders to effectively "flutter" from side to side as they move through air.
在棒球或者足球运动中,由于棒球或者足球表面的粗糙程度不同,存在缝线,会导致产生一种蝴蝶球(kunckball)。 这种球其自旋速度比较慢,但其产生的运动轨迹千变万化,难以捉摸。
其运动规律为
没有自旋的情况如下图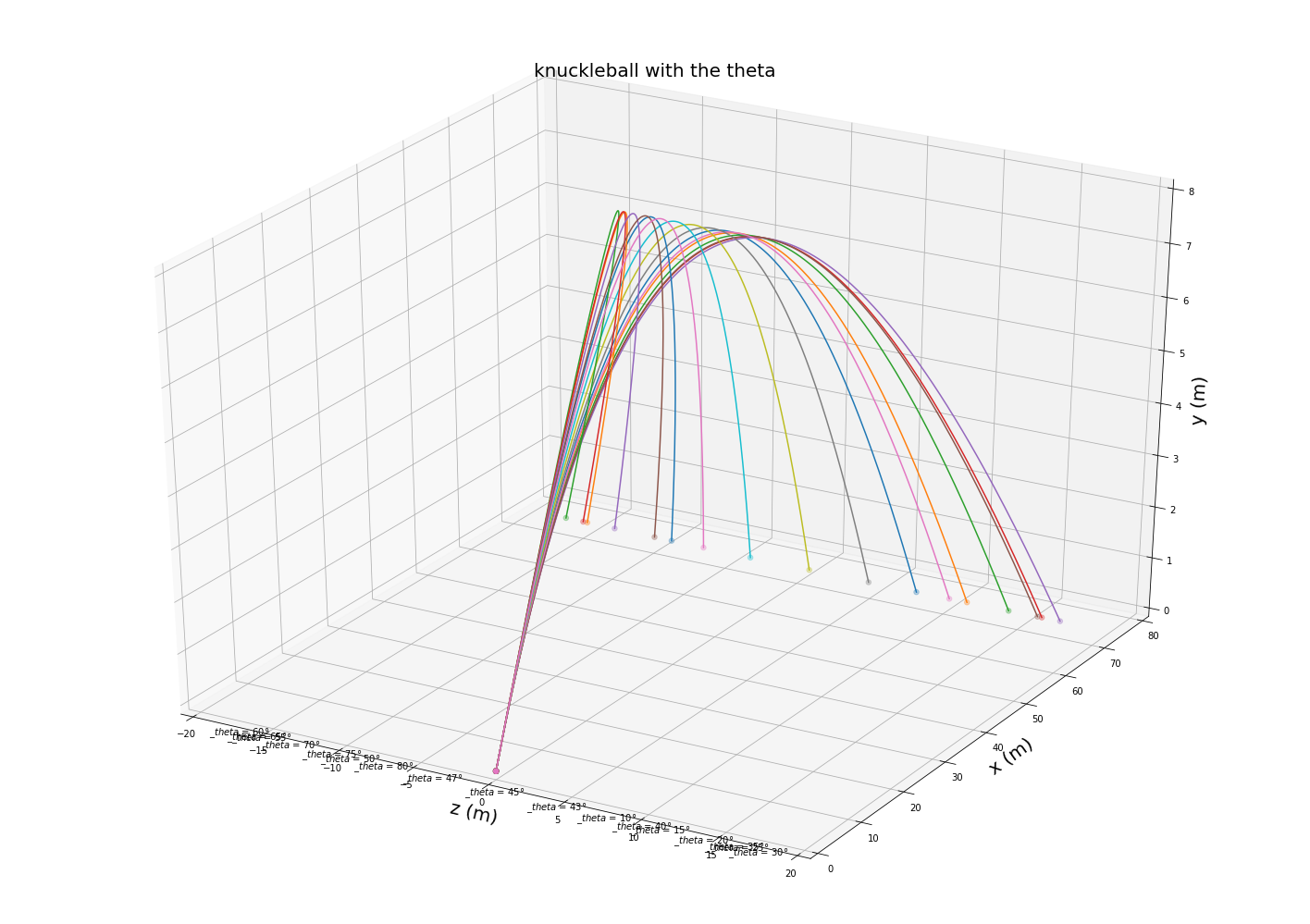
程序如下
import math
import matplotlib.pyplot as plt
def v_x0(v,angle):
v_x0=v*math.cos(math.radians(angle))
return v_x0
def v_y0(v,angle):
v_y0=v*math.sin(math.radians(angle))
return v_y0
def B2(v):
B2_m_=0.0039+0.0058/(1+math.exp((v-35)/5))
return B2_m_
def Fl_m(angles):
#偏转力#
angle=math.radians(angles)
a=math.sin(4*angle)
b=math.sin(8*angle)
c=math.sin(12*angle)
d=math.sin(16*angle)
F_lateral=0.5*(a-0.25*b+0.08*c-0.025*d)
F=F_lateral*9.8
return F
def v(v_x,v_y,v_z):
v=math.sqrt(v_x**2+v_y**2+v_z**2)
return v
class KNUCKLEBALL(object):
def __init__(self,_v,_angle,_theta,_omg=0):
self.v_x=[]
self.v_x0=v_x0(_v,_angle)
self.v_x.append(self.v_x0)
self.v_y=[]
self.v_y0=v_y0(_v,_angle)
self.v_y.append(self.v_y0)
self.v_z=[]
self.v_z.append(0)
self.v=[]
self.v.append(_v)
self.x=[]
self.x.append(0)
self.y=[]
self.y.append(0)
self.z=[]
self.z.append(0)
self.theta=[]
self.theta.append(_theta)
self.omg=_omg
self.B2=[]
self.B2.append(B2(_v))
self.Fl=[]
self.Fl.append(Fl_m(_theta))
self.dt=0.01
self.g=9.8
def calculate(self):
i=0
while self.y[i]>=0:
self.v_x.append(self.v_x[i]-self.B2[i]*self.v[i]*self.v_x[i]*self.dt)
self.x.append(self.x[i]+self.v_x[i]*self.dt)
self.v_y.append(self.v_y[i]-self.g*self.dt-self.B2[i]*self.v[i]*self.v_y[i]*self.dt)
self.y.append(self.y[i]+self.v_y[i]*self.dt)
self.v_z.append(self.v_z[i]+self.Fl[i]*self.dt)
self.z.append(self.z[i]+self.v_z[i]*self.dt)
self.v.append(v(self.v_x[i+1],self.v_y[i+1],self.v_z[i+1]))
self.B2.append(B2(self.v[i]))
self.theta.append(self.theta[i]+self.omg*self.dt)
self.Fl.append(Fl_m(self.theta[i+1]))
i=i+1
def graphics(self,_gra,_theta):
_gra.plot(self.z,self.x,self.y,label=r'$\_theta$ = %d°'%_theta)
_gra.scatter([self.z[0],self.z[-1]],[self.x[0],self.x[-1]],[self.y[0],self.y[-1]],s=30)
_gra.text(self.z[-1], self.x[-1]-80, self.y[-1],r'$\_theta$ = %d°'%_theta ,fontsize=10)
fig=plt.figure(figsize=(18,18))
ax=plt.subplot(1,1,1,projection='3d')
for theta in [10,20,30,40,43,45,47,50,60,70,80]:
knuckleball=KNUCKLEBALL(40.2336,20,theta,0)
knuckleball.calculate()
knuckleball.graphics(ax,theta)
ax.set_xlabel('z (m)', fontsize=20)
ax.set_ylabel('x (m)', fontsize=20)
ax.set_zlabel('y (m)', fontsize=20)
ax.set_title('knuckleball with the theta', fontsize=20)
ax.set_xlim(-20,20)
ax.set_ylim(0,80)
ax.set_zlim(0,8)
plt.show(fig)
分析图中数据可知在无自旋情况下存在两个角度使得其脱离原方向的距离最大。角度为42度时不发生偏转。
有自旋的情况如下图所示
程序如下
import math
import matplotlib.pyplot as plt
def v_x0(v,angle):
v_x0=v*math.cos(math.radians(angle))
return v_x0
def v_y0(v,angle):
v_y0=v*math.sin(math.radians(angle))
return v_y0
def B2(v):
B2_m_=0.0039+0.0058/(1+math.exp((v-35)/5))
return B2_m_
def Fl_m(angles):
#偏转力#
angle=math.radians(angles)
a=math.sin(4*angle)
b=math.sin(8*angle)
c=math.sin(12*angle)
d=math.sin(16*angle)
F_lateral=0.5*(a-0.25*b+0.08*c-0.025*d)
F=F_lateral*9.8
return F
def v(v_x,v_y,v_z):
v=math.sqrt(v_x**2+v_y**2+v_z**2)
return v
class KNUCKLEBALL(object):
def init(self,_v,_angle,_theta,_omg=0):
self.v_x=[]
self.v_x0=v_x0(_v,_angle)
self.v_x.append(self.v_x0)
self.v_y=[]
self.v_y0=v_y0(_v,_angle)
self.v_y.append(self.v_y0)
self.v_z=[]
self.v_z.append(0)
self.v=[]
self.v.append(_v)
self.x=[]
self.x.append(0)
self.y=[]
self.y.append(0)
self.z=[]
self.z.append(0)
self.theta=[]
self.theta.append(_theta)
self.omg=_omg
self.B2=[]
self.B2.append(B2(_v))
self.Fl=[]
self.Fl.append(Fl_m(_theta))
self.dt=0.01
self.g=9.8
def calculate(self):
i=0
while self.y[i]>=0:
self.v_x.append(self.v_x[i]-self.B2[i]*self.v[i]*self.v_x[i]*self.dt)
self.x.append(self.x[i]+self.v_x[i]*self.dt)
self.v_y.append(self.v_y[i]-self.g*self.dt-self.B2[i]*self.v[i]*self.v_y[i]*self.dt)
self.y.append(self.y[i]+self.v_y[i]*self.dt)
self.v_z.append(self.v_z[i]+self.Fl[i]*self.
由图中数据可以得出自转速度不同其运动轨迹也不同
结论 从图中可以看出自转速度,出手时的角度不同都会对蝴蝶球的运动轨迹产生较大影响。
致谢感谢康杰航同学对代码的编写的帮助
