计算物理期末作业

混沌（chaos)现象最初是由气象学家爱德华·罗伦兹通过计算机进行天气模拟时 无意中发现的。在其所描绘的天气动力学系统中，初始条件下的微小变动能够产生巨大的连锁反应，从而使的天气模式发生巨大的变化。又有人将此称为蝴蝶效应。

这是洛伦兹当时提出的方程 虽然现在看来这个方程描述天气有些过于简化了，但它却保留了最基本的情况。 其中r是表示温差影响x,y,z分别表示空气温度、密度、速度。这是取σ=10，r=30,b=8/3时的图形 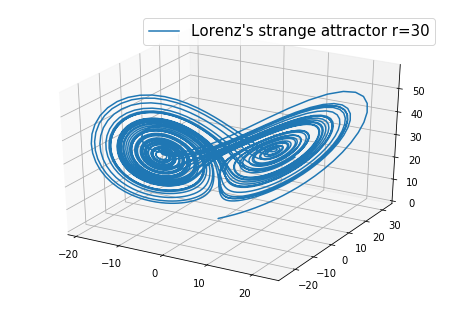程序如下 import matplotlib as mpl

from mpl_toolkits.mplot3d import Axes3D
#import numpy as np
import matplotlib.pyplot as plt
xs, ys, zs = [], [], []
def mkPoints():
σ,r,b = 10.0, 30, 8.0 / 3.0
h = 0.001
x0, y0, z0 = 0.1, 0, 0
    for i in range(5000):
    x1 = x0 + h * σ * (y0 - x0)
    y1 = y0 + h * (x0 * (r - z0) - y0)
    z1 = z0 + h * (x0 * y0 - b * z0)
    x0, y0, z0 = x1, y1, z1
    xs.append(x0)
    ys.append(y0)
    zs.append(z0)
if __name__ == "__main__":
mpl.rcParams["legend.fontsize"] = 15
fig = plt.figure()
ax = Axes3D(fig)
mkPoints()
ax.plot(xs, ys, zs, label = "Lorenz's strange attractor r=30")
ax.legend()
plt.show()`

这是洛伦兹方程所描绘的图形，即洛伦兹双吸引子。尽管Lorenz系统起源于大气对流模型，但实际上他是几个物理系统的共同简化模型，如激光装置及几个相关的对流问题。

另外Rössler attractor是一组三元非线性微分方程代表的吸引子

$\frac{dx}{dt}=-(y+z)$

$\frac{dy}{dt}=x+ay$

$\frac{dz}{dt}=z(x-c)+b$

取a=b=0.2 c=5.7画出右图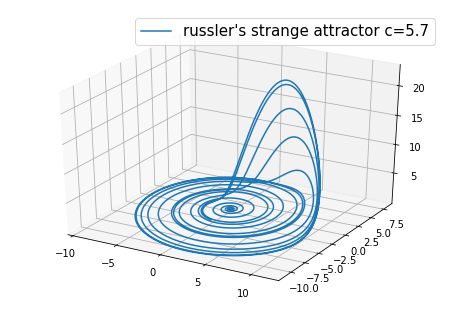 代码如下

import matplotlib as mpl
from mpl_toolkits.mplot3d import Axes3D
#import numpy as np
import matplotlib.pyplot as plt
import math
a=0.2
r=5.7
b=0.2
h=0.001
x0, y0, z0 = 0.1, 0, 0
for i in range(100000):
x1 = x0 - h * (y0 + z0)
    y1 = y0 + h * (x0 +a*y0)
    z1 = z0 + h * (z0*(x0-r)+b)
    x0, y0, z0 = x1, y1, z1
    xs.append(x0)
    ys.append(y0)
    zs.append(z0)
    if __name__ == "__main__":
mpl.rcParams["legend.fontsize"] = 15
fig = plt.figure()
ax = Axes3D(fig)
mkPoints()
ax.plot(xs, ys, zs, label = "russler's strange attractor c=5.7")
ax.legend()
plt.show()

rossler系统是一个人为设计的系统，其目的仅仅只是为了得到奇异吸引子的一个模型。事实上可以说rossler吸引子时lorenz模型的模型。

1983年由蔡少棠发表的蔡氏电路也可以表现出标准的混沌理论行为，其电路方程可以简化为

$\frac{dx}{dt}=p(-x+y-f(x))$

$\frac{dy}{dt}=x-y+z$

$\frac{dz}{dt}=-qy$

$f(x)=mx+1/2(m-n)(|x+1|-|x-1|)$

取p=10,q=14.87,m=-0.68,n=-1.27画出下图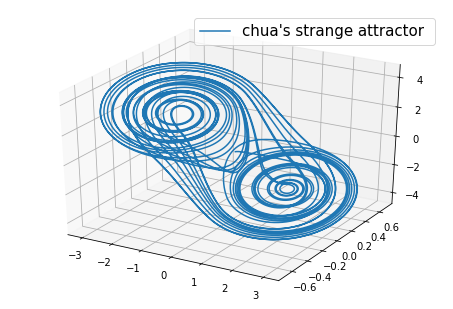 代码如下

import matplotlib as mpl
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import math
xs, ys, zs = [], [], []
p=10.0
q=14.87
m=-0.68
n=-1.27
def mkPoints():
p=10.0
q=14.87
m=-0.68
n=-1.27
h=0.001
x0, y0, z0 = 0.1, 0, 0
for i in range(100000):
x1 = x0 + h * p*(-x0+y0-m*x0-0.5*(n-m)*(abs(x0+1)-abs(x0-1)))
    y1 = y0 + h * (x0-y0+z0)
    z1 = z0 - h * q*y0
    x0, y0, z0 = x1, y1, z1
    xs.append(x0)
    ys.append(y0)
    zs.append(z0)
if name == "main":
mpl.rcParams["legend.fontsize"] = 15
fig = plt.figure()
ax = Axes3D(fig)`

这个图形是双涡旋的混沌吸引子。函数 f(x) 描述了非线性电阻的电子响应。作为一个最简单的实验实现的电路，并且存在一种简单而准确的理论模型相结合，使蔡氏电路成为一个研究混沌理论的许多基础研究和应用的问题的实用系统。二次迭代是确定性动力系统中的混沌最流行和最重要的范例，但同时，它也是奇异的分形之源。

曼德勃罗集是分形中最流行的分形。点集均出自公式$Z_{n+1}=Z_n^2+C$ 对于非线性迭代公式，所有使得无限迭代后的结果能保持有限数值的复数C的集合，构成曼德勃罗集。其图形如下

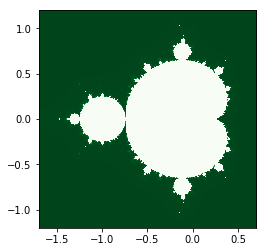代码如下

import numpy as np
import pylab as pl
from matplotlib import cm
def fractal(c):
z = c
for i in range(1, 1000): 
    if abs(z)>5: break
    z = z*z+c
return i
def mandelbrot(cx, cy, d)：
x0, x1, y0, y1 = cx-d, cx+d, cy-d, cy+d 
y,x = np.ogrid[y0:y1:400j,x0:x1:400j]
c = x + y*1j
mandelbrot = np.frompyfunc(fractal,1,1)(c).astype(np.float)
pl.imshow(mandelbrot, cmap=cm.Greens_r, extent=[x0,x1,y0,y1])
mandelbrot(-0.5,0,1.2)
pl.show()

另外当把迭代公式改变时如$z_{n+1}=z_n^3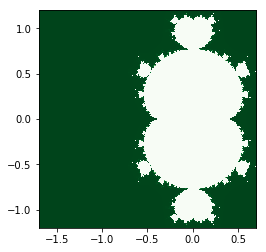+c$ 时图形如右图

而再变为$z_{n+1}=z_n^4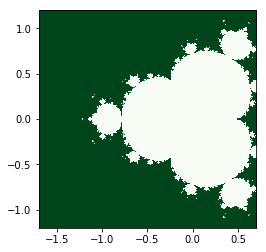+c​$ 时图形如右图

可以看出分形图形与迭代公式有着密切的联系。