第八次作业

homework

3.31 Study the behavior for other tppes of tables. One interesting posibility is a square table with a cicular interior wall located either in the center, or slightly off-center. Another possibility is an elliptical table.

摘要

视为质点的刚性球在不同的边界条件下来回碰撞边界，由物理学定理及计算机模拟得出其运动轨迹，改变其初始条件可以看出不同的轨迹，进而得出混沌的现象。

质点与边界碰撞时发生弹性碰撞，速度方向会发生改变
$v_i,_⊥= (v_i ·n)n$
$v_i,_∥=v_i-v_i,_⊥$
$v_f,_⊥=-v_i,_⊥$
$v_f,_∥=v_i,_∥$
n为碰撞点的法向量可$令n=ai+bj$
又有$dx/dt=v_x, dy/dt=v_y$
式子联立便可得出结果。
碰撞轨迹及相图如图所示
矩形时 $v_x/v_y=0.5$
$v_x/v_y=π$
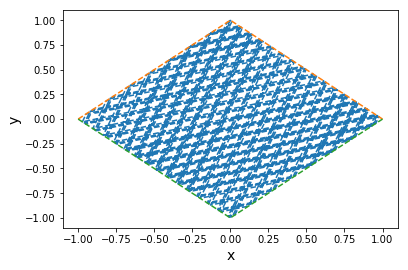
有缺陷的圆 α=0.01时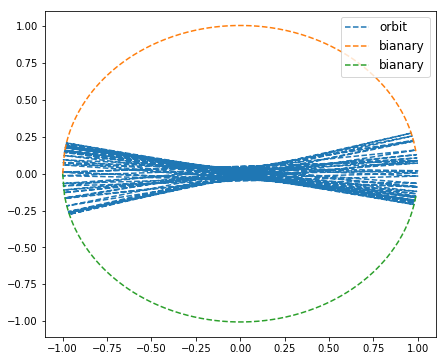
α=0.1
α=0时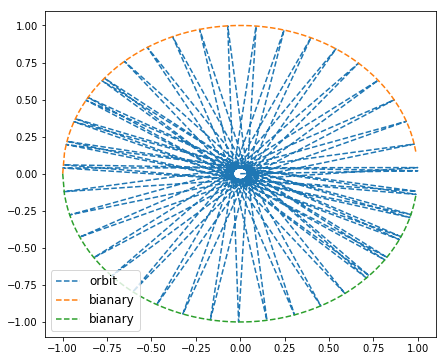
相图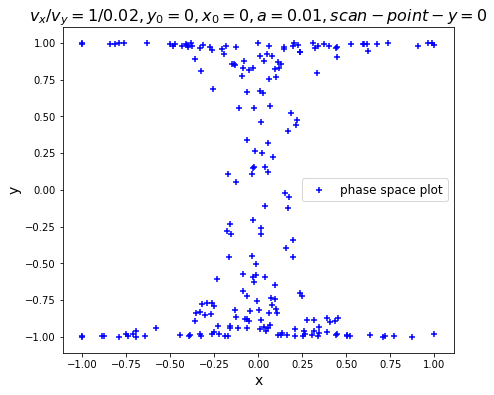


椭圆的碰撞轨迹如图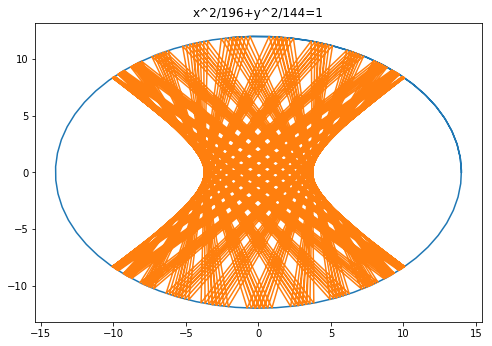
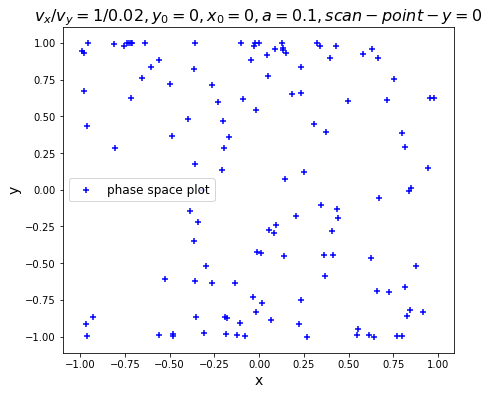
相图如图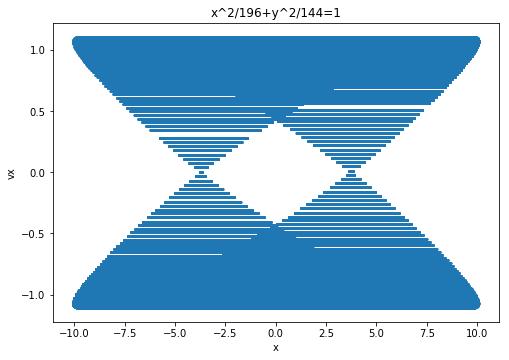
由图可以看出在有对称性破缺的几何图形中碰撞其运动轨迹会发生混沌

import math
x_0=0.2
y_0=0
v_x_0=0.1
v_y_0=v_x_0*math.pi
dt=0.01
end_t=500
x=[]
y=[]
v_x=[]
v_y=[]
t=[]
x.append(x_0)
y.append(y_0)
v_x.append(v_x_0)
v_y.append(v_y_0)
t.append(0)

for i in range(int(end_t/dt)):
x.append(x[i]+v_x[i]*dt)
y.append(y[i]+v_y[i]*dt)
v_x.append(v_x[i])
v_y.append(v_y[i])
t.append(t[i]+dt)
#print abs(x[i+1])+abs(y[i+1])
if  abs(x[i+1])+abs(y[i+1])>1:
    while abs(abs(x[i+1])+abs(y[i+1])-1)>0.00001:
          X=(x[i]+x[i+1])/2
          Y=(y[i]+y[i+1])/2
          a=(2**0.5/2.0)*abs(X)/X
          b=(2**0.5/2.0)*abs(Y)/Y 
          v_x[i+1]=(1-2*a**2)*v_x[i]-2*a*b*v_y[i]
          v_y[i+1]=(1-2*b**2)*v_y[i]-2*a*b*v_x[i]
          #v_y[i+1]=-((2.0*a**3-2.0*a)/b)*v_x[i+1]-(2*a**2-1)*v_y[i+1]
          if abs(X)+abs(Y)>1:
             x[i+1]=X
             y[i+1]=Y
             continue
          else:
             x[i]=X
             y[i]=Y
             continue
    #if abs(abs(X)+abs(Y)-1)<0.1:
      # break


x_1=[-1]
y_1=[0]
x_2=[-1]
y_2=[0]
dx=0.1
for j in range(20):
x_1.append(x_1[j]+dx)
y_1.append(1-abs(x_1[j+1]))
x_2.append(x_1[j]+dx)
y_2.append(-(1-abs(x_1[j+1])))


import matplotlib.pyplot as plt
import numpy as np
import math
plt.plot(x,y,'--' ,label='orbit')
plt.plot(x_1,y_1,'--',label='bianary')
plt.plot(x_2,y_2,'--',label='bianary')
plt.title(u'',fontsize=14)
plt.xlabel(u'x',fontsize=14)
plt.ylabel(u'y',fontsize=14)
plt.legend(fontsize=12,loc='best')
plt.show()
程序2
import numpy as np
from pylab import*
import math
m=14
n=12
def calculatea(vx,vy,x,y):
g=m*m*y*y+n*n*x*x
a=vx-2*n*n*x*x*vx/g-m*n*2*x*y*vy/g
return a
def calculateb(vx,vy,x,y):
g=m*m*y*y+n*n*x*x
b=-vy-m*n*2*x*y*vx/g+n*n*2*x*x*vy/g
return b
x=[1.6]
y=[2.1]
vx=[1.1]
vy=[1]
sx=[]
sy=[]
svx=[]
svy=[]
t=[0]
dt=0.01
sdt=0.0003

i=0
while t[i]<4000.01:
X=x[-1]+vx[-1]*dt
Y=y[-1]+vy[-1]*dt
if X*X/196+Y*Y/144<=1:
    vx.append(vx[-1])
    vy.append(vy[-1])
    x.append(x[-1]+vx[-1]*dt)
    y.append(y[-1]+vy[-1]*dt)
    t.append(t[-1]+dt)
    i=i+1
    if x[-1]*x[-2]<=0:
        sx.append(x[-1])
        sy.append(y[-1])
        svx.append(vx[-1])
else:
    X1=x[-1]+vx[-1]*sdt
    Y1=y[-1]+vy[-1]*sdt
    if X1*X1/196+Y1*Y1/144<=1:
        vx.append(vx[-1])
        vy.append(vy[-1])
        x.append(x[-1]+vx[-1]*sdt)
        y.append(y[-1]+vy[-1]*sdt)
        t.append(t[-1]+sdt)
        i=i+1
        if x[-1]*x[-2]<=0:
            sx.append(x[-1])
            sy.append(y[-1])
            svx.append(vx[-1])
    else:
        #print("vx",vx[-1],"vy",vy[-1],"x",x[-1],"y",y[-1])
        a=calculatea(vx[-1],vy[-1],x[-1],y[-1])
        b=calculateb(vx[-1],vy[-1],x[-1],y[-1])
        vx.append(a)
        vy.append(b)
        x.append(x[-1]+vx[-1]*sdt)
        y.append(y[-1]+vy[-1]*sdt)
        t.append(t[-1]+sdt)
        i=i+1
        if x[-1]*x[-2]<=0:
            sx.append(x[-1])
            sy.append(y[-1])
            svx.append(vx[-1]) 
c=[]
d=[]
theata=[]
theata.append(0)
while theata[-1]<8:
c.append(14*math.cos(theata[-1]))
d.append(12*math.sin(theata[-1]))
theata.append(theata[-1]+0.1)
plt.figure(figsize=(8,5.5))
plt.plot(c,d)
plt.plot(x,y)
#plt.scatter(sy,svx)
#plt.scatter(x,vx,2)
plt.title("x^2/196+y^2/144=1")
#plt.xlabel("x")
#plt.ylabel("vx")
plt.show()
感谢康杰航同学对对椭圆的代码编写的帮助