笛卡尔定理

计算几何

---

一个大圆$O_1$和三个小圆$O_2、O_3、O_4$内切，三个小圆相互外切，他们的半径满足如下等式：

$$(\frac{1}{r_2} + \frac{1}{r_3} + \frac{1}{r_4} - \frac{1}{r_1})^2 = 2(\frac{1}{r^2_1}+\frac{1}{r^2_2}+\frac{1}{r^2_3}+\frac{1}{r^2_4})$$

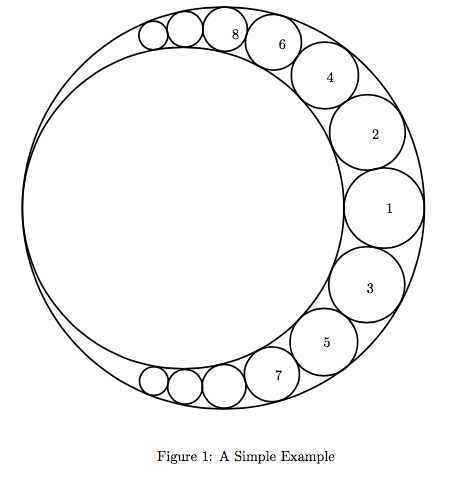
计算有标号圆的面积。
设大圆半径为$r_a$，左边的圆半径为$r_b$。则$r_1 = r_a - r_b$
只看上半部分的圆，对圆重新编号为1、2、3、……
$r_1 = r_a - r_b$
设第$k$个圆的半径为$r_k$，根据笛卡尔定理有如下等式

$$(\frac{1}{r_k}+\frac{1}{r_{k+1}}+\frac{1}{r_b}-\frac{1}{r_a})^2= 2(\frac{1}{r^2_k}+\frac{1}{r^2_{k+1}}+\frac{1}{r^2_b}+\frac{1}{r^2_a})$$
同时也有
$$(\frac{1}{r_k}+\frac{1}{r_{k-1}}+\frac{1}{r_b}-\frac{1}{r_a})^2= 2(\frac{1}{r^2_k}+\frac{1}{r^2_{k-1}}+\frac{1}{r^2_b}+\frac{1}{r^2_a})$$
上下两式相减，得到
$$(\frac{1}{r_{k+1}}-\frac{1}{r_{k-1}})(\frac{2}{r_k}+\frac{1}{r_{k+1}}+\frac{1}{r_{k-1}}+\frac{2}{r_b}-\frac{2}{r_a})= 2(\frac{1}{r^2_{k+1}} - \frac{1}{r^2_{k-1}})$$
将右边展开，得到
$$(\frac{1}{r_{k+1}}-\frac{1}{r_{k-1}})(\frac{2}{r_k}+\frac{1}{r_{k+1}}+\frac{1}{r_{k-1}}+\frac{2}{r_b}-\frac{2}{r_a})= 2(\frac{1}{r_{k+1}}-\frac{1}{r_{k-1}})(\frac{1}{r_{k+1}}+\frac{1}{r_{k-1}})$$
两边同时消去$(\frac{1}{r_{k+1}}-\frac{1}{r_{k-1}})$，得到
$$\frac{2}{r_k}+\frac{1}{r_{k+1}}+\frac{1}{r_{k-1}}+\frac{2}{r_b}-\frac{2}{r_a}= \frac{2}{r_{k+1}}+\frac{2}{r_{k-1}}$$
合并同类项，得到
$$\frac{2}{r_k}+\frac{2}{r_b}-\frac{2}{r_a}=\frac{1}{r_{k+1}}+\frac{1}{r_{k-1}}$$
移项得到
$$\frac{1}{r_{k+1}}=\frac{2}{r_k}+\frac{2}{r_b}-\frac{2}{r_a}-\frac{1}{r_{k-1}}$$
这是一个关于$r_k$的递推式，知道前两项就能递推出后一项。
但是现在只知道$r_1、r_a、r_b$，还不知道$r_2$，无法进行递推。
根据笛卡尔定理有
$$(\frac{1}{r_1} + \frac{1}{r_2} + \frac{1}{r_b} - \frac{1}{r_a})^2 = 2(\frac{1}{r^2_1}+\frac{1}{r^2_2}+\frac{1}{r^2_b}+\frac{1}{r^2_a})$$
将其左右展开有
$$\frac{1}{r^2_2} + 2 \times \frac{1}{r_2}(\frac{1}{r_1} + \frac{1}{r_b} - \frac{1}{r_a}) = 2 \times \frac{1}{r^2_2} + 2(\frac{1}{r^2_1}+\frac{1}{r^2_b}+\frac{1}{r^2_a})$$
移项合并同类型，得到如下
$$\frac{1}{r^2_2} - 2(\frac{1}{r_1} + \frac{1}{r_b} - \frac{1}{r_a})\frac{1}{r_2} +2(\frac{1}{r^2_1}+\frac{1}{r^2_b}+\frac{1}{r^2_a}) = 0$$
将$\frac{1}{r_2}$看作未知量，根据实际情况，方程的两个根应该相同，所以根据韦达定理有
$$\frac{1}{r_2} + \frac{1}{r_2} = 2(\frac{1}{r_1} + \frac{1}{r_b} - \frac{1}{r_a})$$
则
$$\frac{1}{r_2} = \frac{1}{r_1} + \frac{1}{r_b} - \frac{1}{r_a}$$
已经求得$r_1$和$r_2$，可以进行递推