第十次作业：洛伦兹模型

臧之昊 2013301020056

1、背景

洛伦兹研究流体力学的基本方程，也就是$Navier-Stokes$方程组，这个方程组是一个关于位置和时间的十分复杂的微分方程集合，描述了速度、温度、密度等等，但是在实际中它的解析解是十分难求解的。

为了解决这个问题，使得计算的方法能够行得通，洛伦兹做了一些工作，这也被称作$Rayleigh-B\acute{e}nard$问题,这个问题仅仅考虑在一个顶部与底部温度不同的容器中的流体，并且温度差还在不断增加，这样流体就会经历从静止状态到稳定运动状态再到混沌状态的变化。

2、正文

事实上，洛伦兹将这个问题极大地简化了，最后只有如下三个方程： $$\frac{{\rm d}x}{{\rm d}t}=\sigma(y-x)$$ $$\frac{{\rm d}y}{{\rm d}t}=-xz+rx-y$$ $$\frac{{\rm d}z}{{\rm d}t}=xy-bz$$

这三个方程现在也被称为洛伦兹方程组，其中$\sigma$、$r$、$b$是描述流体中温度变化或阻尼的几个参量，通过这个模型可以观察到混沌效应。

1）设定初始状态$x=1,y=z=0,\si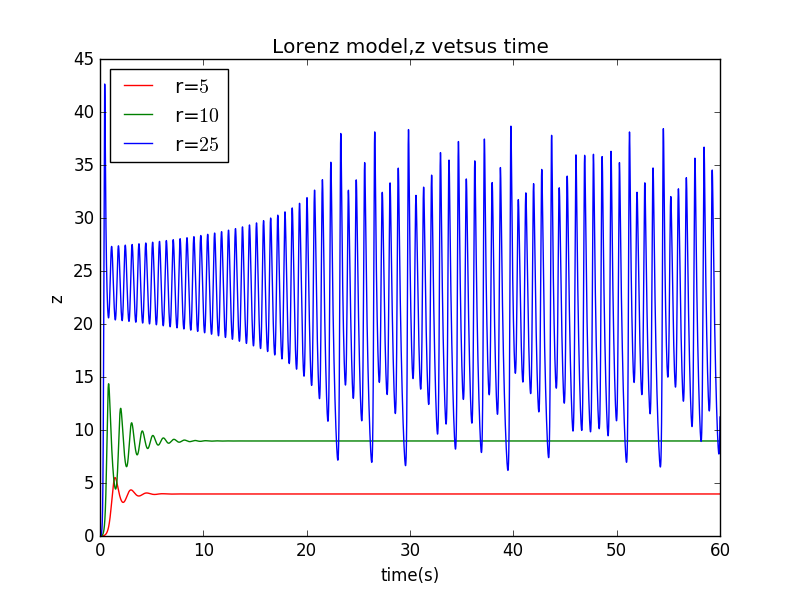gma=10,b=8/3$,改变$r$值观察$z-t$关系：

从图中可以看出当$r=5$时，$z$随时间衰减，最后保持在一个定值；当然，在$r=10$时，情况也是一样，只不过衰减的时间长了一点。但当$r=25$时，情况就完全不一样，一开始的瞬变现象还是大概是周期变化的，但是大概到了$t=20s$之后，它的运动就变得不规律了。

2）保持$r=25$和另外两个参量不变，初始条件为$x=1,y=z=0$，得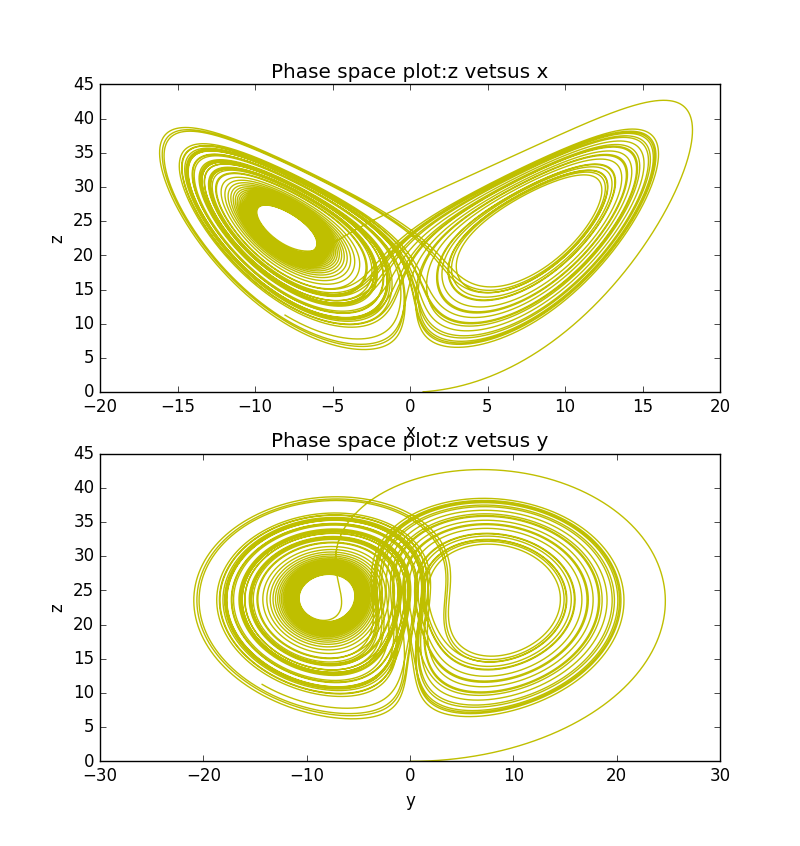到如下$x-z,y-z$模型：

可以看出系统在$x=0$的一侧要经历类似于周期性的振动，然后运动到另一侧经历一系列新的振动。

3）我们还可以作出截面图：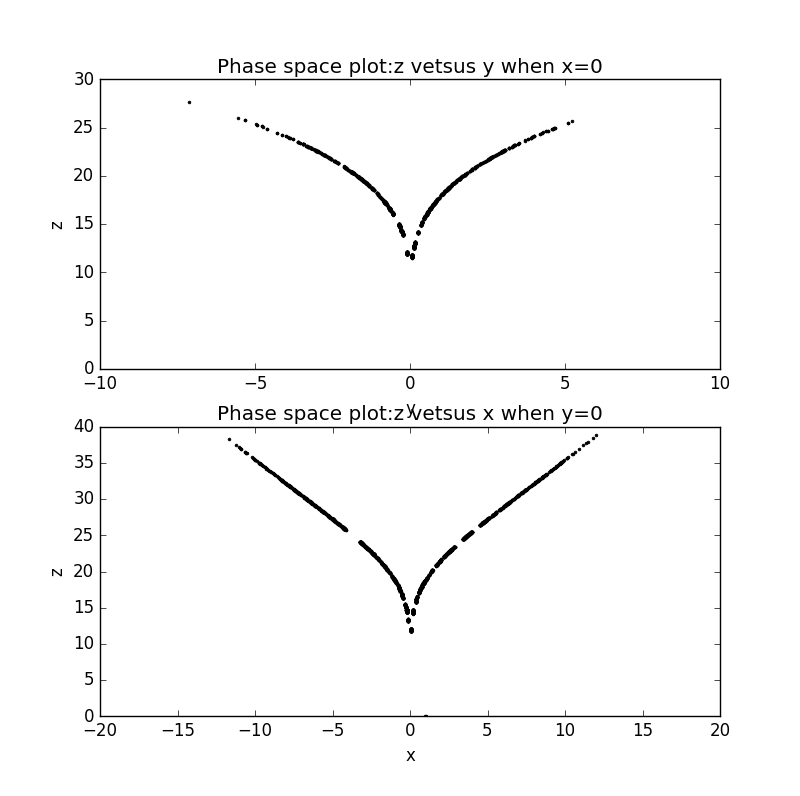

尽管运动行为是十分混乱的，但是在相空间中的轨迹是十分有规律可循的。通过这两个图可以发现相空间中吸引子的表面可以认为是与初始条件无关的。因此，尽管与时间有关的行为是不可预测的，但是我们可以预测相空间中系统在吸引子的表面某处。

4）其他条件不变，增大$r$值至$160$左右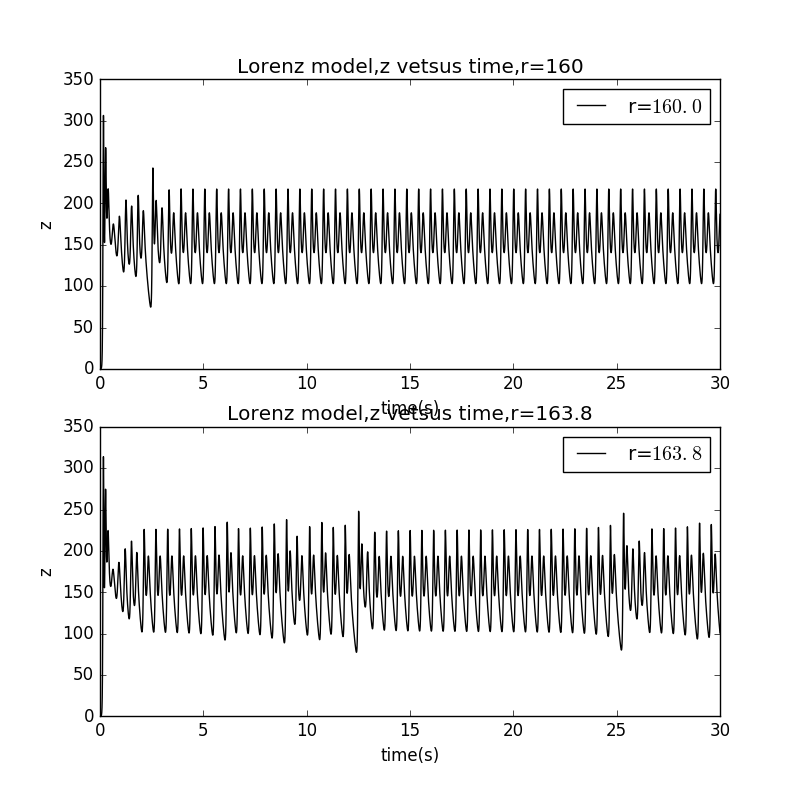，有如下图：

可以看出$r=160$时，几乎是周期性运动，然后$r=163.8$时，又有一些混沌现象产生。

3、总结

本文讨论了不同$r$值情况下的洛伦兹模型，随着$r$的变化，模型也会有混沌-周期-混沌的变化，说明洛伦兹模型对于初始条件是十分敏感的，然而它在相空间的吸引子表面的轨迹是不随初始条件变化的。

4、致谢

感谢钟惠舟同学的程序。