@cybercser 2015-11-18T12:44:10.000000Z 字数 5883 阅读 72

第八课：基本着色

第八课：基本着色

OpenGL 教程

在第八课中，我们将学习基本的着色方法。包括：

物体离光源越近会越亮
直视反射光时会有高亮（镜面反射）
当光没有直接照射物体时，物体会更暗（漫反射）
用环境光简化计算

不包括：

阴影。这个主题涵盖甚广，必须开设专题教程。
类镜面反射（包括水）
任何复杂的光与物质的相互作用，像次表面散射（subsurface scattering）（比如蜡）
各向异性材质（比如拉丝金属（brushed metal））
追求真实感的，基于物理的着色（Physically-based shading）
环境遮挡（Ambient Occlusion）（凹陷处显得更暗）
辉映（Color Bleeding）（一块红色的地毯会在白色天花板上映出红色）
透明
各种全局光照（Global Illumination）（以上各种技术的总称）

总而言之：只讲基础知识。

法线

前面的教程中我们一直在处理法线，但是并不知道法线到底是什么。

三角形法线

一个平面的法线是一个长度为1并且垂直于这个平面的向量。
一个三角形的法线是一个长度为1并且垂直于这个三角形的向量。通过简单地将三角形两条边进行叉乘计算（向量a和b的叉乘结果是一个同时垂直于a和b的向量，还记得吗？），然后归一化：使长度为1。伪代码如下：

triangle ( v1, v2, v3 )
edge1 = v2-v1
edge2 = v3-v1
triangle.normal = cross(edge1, edge2).normalize()

不要将法线(normal)和normalize()混淆。Normalize()是让一个向量（任意向量，不一定是法线）除以其长度，从而使新长度为1。法线(normal)则是某一类向量的名字。

顶点法线

引申开来：顶点的法线，是包含该顶点的所有三角形的法线的均值。这带来了不少便利——因为在顶点着色器中，我们处理顶点，而不是三角形；所以最好把信息放在顶点上。况且在OpenGL中，我们没有任何办法获得三角形信息。伪代码如下：

vertex v1, v2, v3, ....
triangle tr1, tr2, tr3 // all share vertex v1
v1.normal = normalize( tr1.normal + tr2.normal + tr3.normal )

在OpenGL中使用顶点法线

在OpenGL中使用法线很简单。法线是顶点的属性，就像位置，颜色，UV坐标等一样；按处理其他属性的方式处理即可。第七课的loadOBJ函数已经将它们从OBJ文件中读出来了。

     GLuint normalbuffer;
     glGenBuffers(1, &amp;normalbuffer);
     glBindBuffer(GL_ARRAY_BUFFER, normalbuffer);
     glBufferData(GL_ARRAY_BUFFER, normals.size() * sizeof(glm::vec3), &normals[0], GL_STATIC_DRAW);

和

     // 3rd attribute buffer : normals
     glEnableVertexAttribArray(2);
     glBindBuffer(GL_ARRAY_BUFFER, normalbuffer);
     glVertexAttribPointer(
         2,                                // attribute
         3,                                // size
         GL_FLOAT,                         // type
         GL_FALSE,                         // normalized?
         0,                                // stride
         (void*)0                          // array buffer offset
     );

有这些准备就可以开始了。

漫反射（Diffuse）分量

表面法线的重要性

当光源照射一个物体，其中重要的一部分光向各个方向反射。这就是“漫反射分量”。（我们稍后会看到光的其他分量）

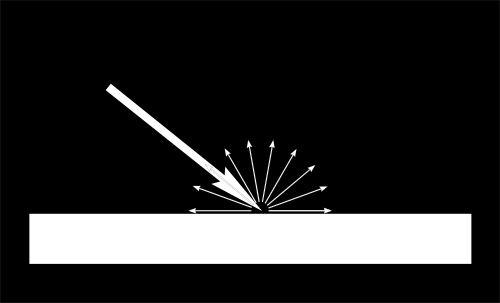
diffuseWhite

当一定量的光线到达某表面，该表面根据光到达时的角度而不同程度地被照亮。

如果光线垂直于表面，它将汇聚在一小片表面上。如果同等强度的光线以一个倾斜角到达表面，则其照亮的面积更大：

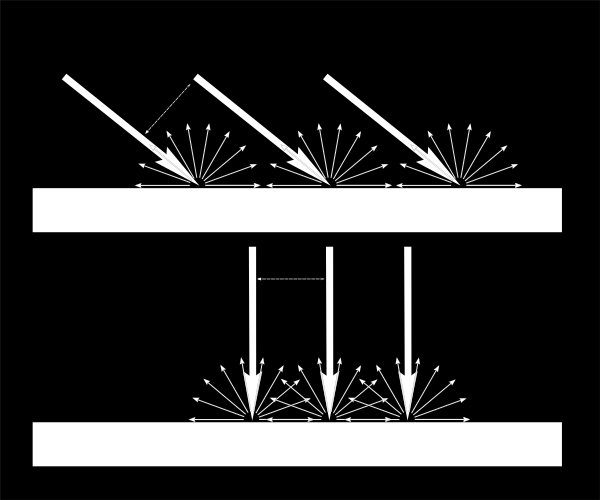
diffuseAngle

这意味着斜射下的表面各点会较暗（但请记住，更多的点会被照射到，总光强度仍然是一样的）

也就是说，当计算像素的颜色时，入射光和表面法线的夹角很重要。故有：

    // Cosine of the angle between the normal and the light direction,
    // clamped above 0
    //  - light is at the vertical of the triangle -> 1
    //  - light is perpendicular to the triangle -> 0
    float cosTheta = dot( n,l );
    color = LightColor * cosTheta;

在这段代码中，n是表面法线，l是从表面到光源的单位向量（和光线方向相反。虽然不直观，但能简化数学计算）。

注意正负号

求cosTheta的公式有漏洞。如果光源在三角形后面，n和l方向相反，那么n.l是负值。这意味着colour将是一个负值，没有意义。因此这种情况下必须用clamp()将cosTheta截取为0：

    // Cosine of the angle between the normal and the light direction,
    // clamped above 0
    //  - light is at the vertical of the triangle -> 1
    //  - light is perpendicular to the triangle -> 0
    //  - light is behind the triangle -&gt; 0
    float cosTheta = clamp( dot( n,l ), 0,1 );
    color = LightColor * cosTheta;

材质颜色

当然，输出颜色也受材质颜色的影响。在下图中，白光由绿、红、蓝光组成。当光碰到红色材质时，绿光和蓝光被吸收，只有红光得以保留。

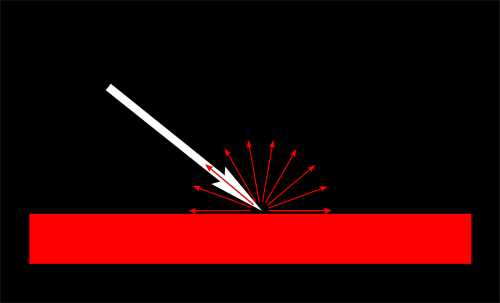
diffuseRed

我们可以用一个简单的乘法来建模：

    color = MaterialDiffuseColor * LightColor * cosTheta;

建立光照模型

首先假设在空间中有一个点光源，它像蜡烛一样向所有方向发射光线。

对于该光源，我们的表面收到的光通量（luminous flux）依赖于表面到光源的距离：越远光越少。实际上，光通量与距离的平方成反比：

    color = MaterialDiffuseColor * LightColor * cosTheta / (distance*distance);

最后，需要另一个参数来控制光的强度。我们可以将其作为LightColor（随后的课程中会讲到）的变量，但是现在暂且只含一个颜色值（如白色）和一个强度（如60瓦）。

    color = MaterialDiffuseColor * LightColor * LightPower * cosTheta / (distance*distance);

汇总

我们还需要一些参数（各种颜色和强度）和代码让程序运行起来。

可直接从纹理中获取MaterialDiffuseColor。

通过GLSL的uniform变量在着色器中设置LightColor和LightPower。

cosTheta由n和l决定。我们可以在任意空间中表示它们，最终结果都是一样的。这里选择摄像机空间，是因为在其中计算光源位置比较简单：

    // Normal of the computed fragment, in camera space
     vec3 n = normalize( Normal_cameraspace );
     // Direction of the light (from the fragment to the light)
     vec3 l = normalize( LightDirection_cameraspace );

在顶点着色器中计算Normal_cameraspace和LightDirection_cameraspace，然后传给片段着色器：

    // Output position of the vertex, in clip space : MVP * position
    gl_Position =  MVP * vec4(vertexPosition_modelspace,1);
    // Position of the vertex, in worldspace : M * position
    Position_worldspace = (M * vec4(vertexPosition_modelspace,1)).xyz;
    // Vector that goes from the vertex to the camera, in camera space.
    // In camera space, the camera is at the origin (0,0,0).
    vec3 vertexPosition_cameraspace = ( V * M * vec4(vertexPosition_modelspace,1)).xyz;
    EyeDirection_cameraspace = vec3(0,0,0) - vertexPosition_cameraspace;
    // Vector that goes from the vertex to the light, in camera space. M is ommited because it's identity.
    vec3 LightPosition_cameraspace = ( V * vec4(LightPosition_worldspace,1)).xyz;
    LightDirection_cameraspace = LightPosition_cameraspace + EyeDirection_cameraspace;
    // Normal of the the vertex, in camera space
    Normal_cameraspace = ( V * M * vec4(vertexNormal_modelspace,0)).xyz; // Only correct if ModelMatrix does not scale the model ! Use its inverse transpose if not.

这段代码看起来很牛，其实就是第三课的所学内容：矩阵。每个向量命名时，都嵌入了所在的空间名，这样在跟踪时更简单。 这种做法值得借鉴。

M和V分别是模型和观察矩阵，并用与MVP完全相同的方式传给着色器。

实战时间

现在有了编写漫反射光源的一切必要条件。赶快动手把它实现出来吧。:)

结果

只有漫反射分量时，我们得到以下结果（呵呵，不好意思，纹理还是这么单调）：

diffuse_only

这次的结果比之前的好，不过还是感觉少了些什么。特别是由于使用了clamp()，Suzanne的背后完全是黑色的。

环境光(Ambient)分量

环境光分量是最具欺骗性的。

我们希望Suzanne的背后有一点亮光，因为在现实生活中灯泡会照亮它背后的墙，而墙会反过来（微弱地）照亮物体的背后。

但计算这种光照的代价大得可怕。

因此通常可以简单地以假的光源代替这种计算。实际中一般直接让三维模型发光，使它看起来不是漆黑一片就行了。

可这样操作：

    vec3 MaterialAmbientColor = vec3(0.1,0.1,0.1) * MaterialDiffuseColor;
    color =
     // Ambient : simulates indirect lighting
     MaterialAmbientColor +
     // Diffuse : "color" of the object
     MaterialDiffuseColor * LightColor * LightPower * cosTheta / (distance*distance) ;

来看看结果

结果

好的，效果变好些了。可以把(0.1,0.1,0.1)换成别的值来获得更好的效果。

diffuse_ambiant

镜面光（Specular）分量

另一个反射光分量就是镜面光分量。这部分光在表面有确定的反射方向。

specular

如图所示，镜面反射光形成了一个波瓣（lobe）。极端情况下，漫反射分量可为零，这时波瓣非常窄（所有的光往一个方向反射），这样就形成了镜子。

（确实可以通过调整参数值得到镜面；但在这个例子中镜面反射的只有光源，渲染结果看起来会很奇怪)

    // Eye vector (towards the camera)
    vec3 E = normalize(EyeDirection_cameraspace);
    // Direction in which the triangle reflects the light
    vec3 R = reflect(-l,n);
    // Cosine of the angle between the Eye vector and the Reflect vector,
    // clamped to 0
    //  - Looking into the reflection > 1
    //  - Looking elsewhere -> < 1
    float cosAlpha = clamp( dot( E,R ), 0,1 );
    color =
        // Ambient : simulates indirect lighting
        MaterialAmbientColor +
        // Diffuse : &quot;color&quot; of the object
        MaterialDiffuseColor * LightColor * LightPower * cosTheta / (distance*distance) ;
        // Specular : reflective highlight, like a mirror
        MaterialSpecularColor * LightColor * LightPower * pow(cosAlpha,5) / (distance*distance);

R是反射光的方向，E是视线的反方向（就像之前对“l”的假设）；如果二者夹角很小，意味着视线与反射光线重合。

pow(cosAlpha,5)用来控制镜面反射的波瓣。可以通过增大第二个参数（译注：镜面高光指数）得到更大的波瓣。

最终结果

diffuse_ambiant_specular

注意观察，由于有了镜面反射，鼻子和眉毛显得更亮了。

这个着色模型得益于其简单性，已经使用多年。但它存在很多问题，因而被microfacet BRDF（bidirectional reflection distribution function，微表面双向反射分布函数）之类的基于物理的（physically-based）模型所取代，这些内容后面会讲到。

下节课是第一节中级课程！我们将学习怎样提高VBO的性能。

© http://www.opengl-tutorial.org/

Written with Cmd Markdown.