离散数学补充 群论（四）

离散数学 群论

Communication

1. 信息的基本单位是报文(message)：一个有限字母表中的有限字符序列。
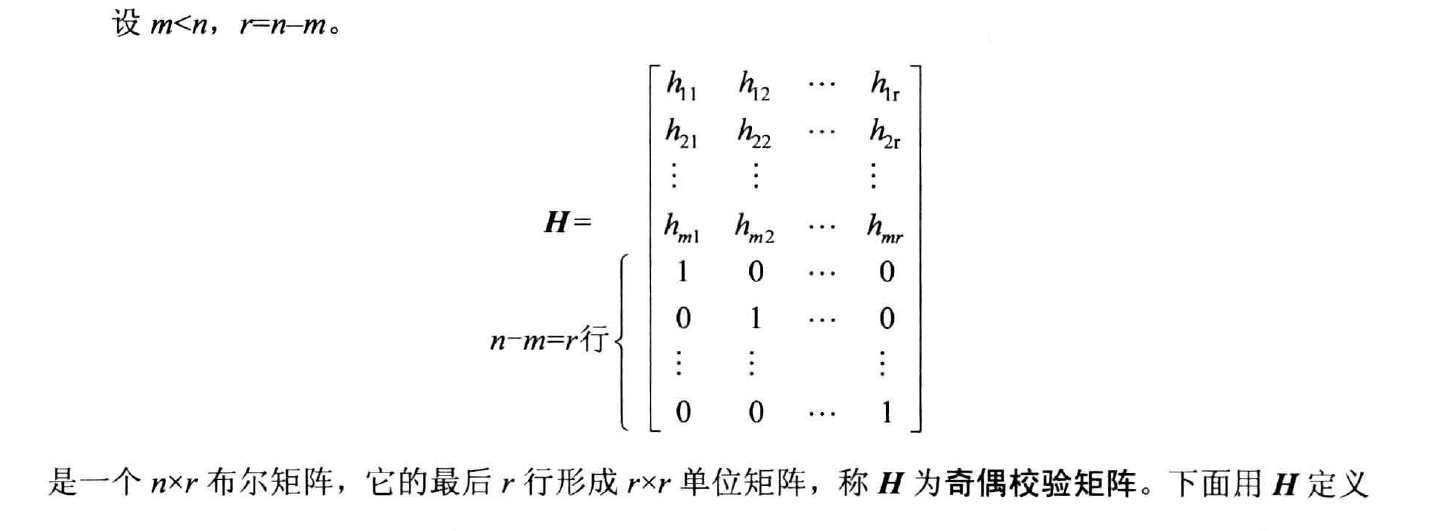
   基本单位：字(word), $m$ 个 0，1组成的序列。
2. 传输通道可能遭到的干扰（噪声）可能引起 $0$ 作为 $1$ 被接收，或者反过来。
3. 选取一个 $n>m$ , 和一个单射(因为不同字应该对应不同的代码字）函数 $e: B^n \rightarrow B^m$, 函数 $e$： 编码函数（encoding function）， $b \in B^m$, $e(b)$: $b$ 的代码字（code word）。
   
   • 如果 $x$ 和 $x_t$ 传输中有至少1个，但不超过 $k$ 个错误，就说 $x = e(b)$ 有 $k$ 个或更少的错误传送 ($k$ or fewer errors)。 如果任何时刻，$x = e(b)$ 都以 $k$ 个或更少错误传送，那么 $x_t$ 不是一个代码字。（否则它会指向另一条信息，因此两个不同的代码子至少有k+1个位不同）则说 $e$ 可以检测到 $k$ 个或更少错误(detect $k$ or fewer errors)。
     
4. 对于 $x \in B^n$， 把其中1的个数称为 $x$ 的权（weight）
5. 奇偶校验码（parity check code)
   
   它不能检测偶数个错误。
6. Hamming distance
   
   其中 $\oplus$ 表示异或，即按位加。
   
   • 距离性质:
     其中性质 $(d)$ 的证明如下：
     
     第一个不等式等号成立条件当且仅当 $a,b$ 所有位都相异。
   • Minimum distance
     
     
     定理2在上面已经被阐释过了。

群码（group code）

一个 $(m,n)$ 编码函数 $e$，如果 $e(B^m) = \{e(b)| b\in B^m\} = Ran(e)$ 是 $B^n$ 的一个子群，那么这个编码函数被称作一个群码。

根据群的性质，

• Theorem 3
  
  定理3 可用来直接计算一个群码的最小距离，而不需要把所有距离计算出来取最小值。
• Theorem 5
  
  略去的定理4说的是布尔积的分配律。
  Corollary 1
  
• 奇偶校验矩阵（parity check matrix）
  
  
• Theorem 6
  
  而根据上述奇偶校验矩阵中编码函数的定义，$x_i = b_1\cdot h_{1i} + b_2\cdot h_{2i}+...b_m\cdot h_{mi}$,则等式两边的字每一位都相同，相加必为0,反过来，相加为0说明每一位都相同，也就相等。故得证。
  Corollary 2
  
  $x*H = \overline 0\Leftrightarrow x = e_H(b)$, 推论1说明了 $N = \{x \in B^n| x*H = \overline 0\}$ 是正规子群， 而 $e_H(B^m) = N$。

Decoding and error correction

• 译码函数（decoding function）
  
  
  
  
  
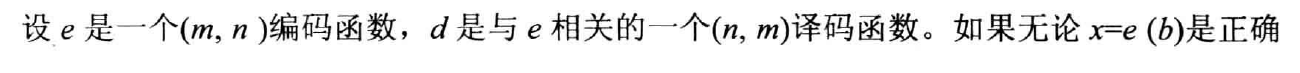
• 最大似然方法（maximum likelihood technique）
  最大似然译码函数（maximum likelihood decoding function)
  
• Theorem 1
  
  因为 $x_t$ 必须和唯一的代码字最接近。
  
  

• 陪集首部（coset leader）
  
  
  如果是群码，可按如下步骤进行：
  
  对于步骤1和步骤2,详细说明如下：
  
  （注：因为$\epsilon$ 和 $y$在同一个等价类中）
  

• 利用上面提到的奇偶校验矩阵可以简化上述步骤。
  由 $f_H(x) = x *H$ 定义的函数 $f_H: B^n \rightarrow B^r$ 是群 $B^n$ 到群 $B^r$ 上的一个同态。

• Theorem 3
  
• 校验子（syndrome）
  
  
  则新步骤如下：
  
  通过做题我对这部分的步骤有了一些经验：
  
  1. 先列出所有的校验子，在前面补上0填满。这样获得的就是处在不同陪集中的字。
  2. 把其中1的个数不满足“最少”的字与 $N$ 取异或（即按位加），在结果中找到1数量最少的字，即为陪集首部；其他满足最少的字本身就是陪集首部。
     (只有1个“1”的字一定是一个陪集首部，所以 2. 中的步骤仅针对不可能只有1个“1”的情况使用就好了）
     这样就能很快完成步骤1和步骤2。