机器学习week2 ex1 review

机器学习 编程作业 吴恩达

• 这周的作业主要关于线性回归。

1. Linear regression with one variable

1.1 Plotting the Data

• 通过已有的城市人口和盈利的数据，来预测在一个新城市营业的收入。
  文件ex1data1.txt包含了以下数据：

  第一列是城市人口数据，第二列是盈利金额（负数代表亏损）。

• 可以首先通过绘图来直观感受。
  这里我们可以使用散点图（scatter plot ）。
  通过 Octave/MATLAB 实现。
  数据存储在ex1data1.txt中，如下图所示：
  
  文件ex1.m将ex1data1.txt中的所有数据载入data：

data = load('ex1data1.txt');      % read comma separated data

Octave/MATLAB 会根据数据文件中的逗号来分隔数据。这里的data以矩阵形式存储。因为有两组数据，所以是两列。
然后分别将人口和盈利存入 $X$ 和 $y$ 中。

X = data(:,1); y = data(:,2);
m = length(y);

$X$ 取data的第一列，$y$ 取第二列。$m$ 是 training example 的数量。因为 $X$ 和 $y$ 大小相同，用哪个都无所谓。

下一步调用 PlotData 函数绘制散点图。
我们需要首先把这个函数补充完整。
这是文件中包含的原始版本：

function plotData
%PLOTDATA Plots the data points x and y into a new figure 
%   PLOTDATA(x,y) plots the data points and gives the figure axes labels of
%   population and profit.
figure; % open a new figure window
% ====================== YOUR CODE HERE ======================
% Instructions: Plot the training data into a figure using the 
%               "figure" and "plot" commands. Set the axes labels using
%               the "xlabel" and "ylabel" commands. Assume the 
%               population and revenue data have been passed in
%               as the x and y arguments of this function.
%
% Hint: You can use the 'rx' option with plot to have the markers
%       appear as red crosses. Furthermore, you can make the
%       markers larger by using plot(..., 'rx', 'MarkerSize', 10);
% ============================================================
end

我们可以看到他要求我们绘制散点图，并给横纵坐标加上 population 和 profit 的标签。
Hint 提示我们这样做：

• 使用figure打开一个图形窗口。
• 使用plot函数绘图。用xlabel和ylabel分别设置横纵坐标的标签。rx将散点设置为红十字形（red cross）。通过'Markersize'，10'设置散点大小。

代码如下：

plot(x, y, 'rx', 'Markersize', 10);           % plot the data
ylabel('Profit in $10,000s');                 % set the y-axis label
xlabel('Population of City in 10,000s');      % set the x-axis label

这时再运行ex1.m,就可以得到如下图形：

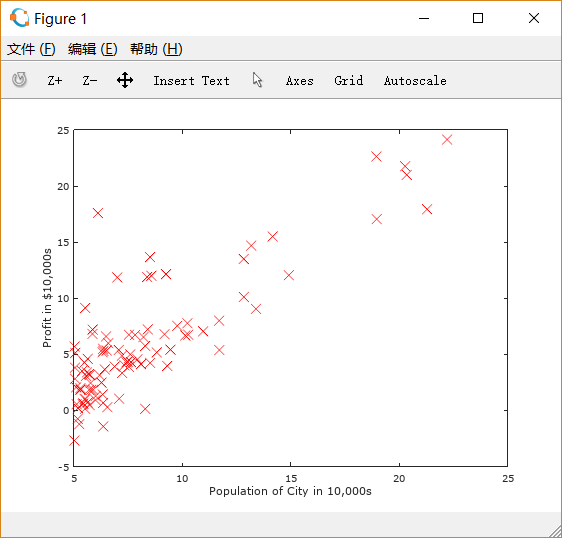
1.2 Gradient Descent

• 通过梯度下降算法计算线性回归参数 $\theta$。
  
  

1.2.1 Update Equations

线性回归的目标就是使代价函数最小
$J(\theta) = \displaystyle{\frac {1} {2m}\sum_{i=1}^{m}}(h_\theta(x^{(i)})-y^{(i)})^2$
其中
$h_\theta(x) = \theta^Tx = \theta_0+\theta_1x_1$

使用批量梯度下降法（batch gradient descent ) 以使 $J(\theta)$ 最小。
$\theta_j := \theta_j -\alpha \displaystyle{\frac{1}{m}\sum_{i=1}^{m}}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}$
( simultaneously update $\theta_j$ for all $j$ )

1.2.2 Implementation

目前的 $X$ 是一个列向量，每一行存储一个 training example，即 $x_1$。
因此在脚本文件ex1.m中，为了处理 $\theta_0$ , 给每一行增加一个 $x_0 = 1$。

X = [ones(m,1) data(:,1)];   % Add a column of ones to x

因为只有一个变量 $x_1$ 影响盈利，
$\theta = \left[ \begin{matrix} \theta _{0}\\\theta _{1}\end{matrix} \right]$
初始化 $\theta$ 为 $\left[ \begin{matrix} 0 \\ 0 \end{matrix} \right]$

theta = zeros(2,1);  % initialize fitting parameters

设置迭代次数和 $\alpha$ 的值：

iterations = 1500;
alpha = 0.01;

1.2.3 Computing the cost $J(\theta)$

根据上述公式，完成computeCost以计算代价函数 $J(\theta)$

function J = computeCost(X, y, theta)
%COMPUTECOST Compute cost for linear regression
%   J = COMPUTECOST(X, y, theta) computes the cost of using theta as the
%   parameter for linear regression to fit the data points in X and y
% Initialize some useful values
m = length(y); % number of training examples
prediction = X * theta;
sqError = (prediction - y).^2;
% You need to return the following variables correctly 
J = 0;
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta
%               You should set J to the cost.
J = 1/(2 * m) * sum(sqError);
% =========================================================================
end

我们来看一下脚本文件ex1.m中这一部分的测试代码

fprintf('\nTesting the cost function ...\n')
% compute and display initial cost
J = computeCost(X, y, theta);
fprintf('With theta = [0 ; 0]\nCost computed = %f\n', J);
fprintf('Expected cost value (approx) 32.07\n');
% further testing of the cost function
J = computeCost(X, y, [-1 ; 2]);
fprintf('\nWith theta = [-1 ; 2]\nCost computed = %f\n', J);
fprintf('Expected cost value (approx) 54.24\n');
fprintf('Program paused. Press enter to continue.\n');
pause;

它对两组数据进行了测试。一组是我们之前初始化后的$\theta = \left[ \begin{matrix} 0 \\ 0 \end{matrix} \right]$ , 另一组是$\left[ \begin{matrix} -1 \\ 2 \end{matrix} \right]$。
如果你的computeCost.m计算正确的话，输出的两个答案应该是32.072734和54.242455。

1.2.4 Gradient descent

• 根据之前的公式
  $\theta_j := \theta_j -\alpha \displaystyle{\frac{1}{m}\sum_{i=1}^{m}}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}$
  ( simultaneously update $\theta_j$ for all $j$ )

补充gradientDescent.m的代码。如下：

%GRADIENTDESCENT Performs gradient descent to learn theta
%   theta = GRADIENTDESCENT(X, y, theta, alpha, num_iters) updates theta by 
%   taking num_iters gradient steps with learning rate alpha
% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
temp = theta;
n = length(theta);
for iter = 1:num_iters
    % ====================== YOUR CODE HERE ======================
    % Instructions: Perform a single gradient step on the parameter vector
    %               theta. 
    %
    % Hint: While debugging, it can be useful to print out the values
    %       of the cost function (computeCost) and gradient here.
    %
    for j = 1:n
        temp(j) = theta(j) - 1/m*alpha*sum((X*theta-y).*X(:,j));
    end;
    theta = temp;
    % ============================================================
    % Save the cost J in every iteration    
    J_history(iter) = computeCost(X, y, theta);
end
end

事实上这已经解决了多变量的线性回归问题，尽管这里只用处理 $n=2$ 的情况。

再来看一下脚本文件里这一部分的内容：

fprintf('\nRunning Gradient Descent ...\n')
% run gradient descent
theta = gradientDescent(X, y, theta, alpha, iterations);
% print theta to screen
fprintf('Theta found by gradient descent:\n');
fprintf('%f\n', theta);
fprintf('Expected theta values (approx)\n');
fprintf(' -3.6303\n  1.1664\n\n');
% Plot the linear fit
hold on; % keep previous plot visible
plot(X(:,2), X*theta, '-')
legend('Training data', 'Linear regression')
hold off  % do not overlay any more plots on this figure
% Predict values for population sizes of 35,000 and 70,000
predict1 = [1, 3.5] *theta;
fprintf('For population = 35,000, we predict a profit of %f\n',...
    predict1*10000);
predict2 = [1, 7] * theta;
fprintf('For population = 70,000, we predict a profit of %f\n',...
    predict2*10000);
fprintf('Program paused. Press enter to continue.\n');
pause;

使用梯度下降法后输出计算得到的 $\theta$:

与正确情况吻合。

之后绘制图线。对之前的散点图使用hold on，保留图形。
再绘制经过梯度下降后得到的 $X$ 和 $h_\theta(x) = X\theta$ 的图线。
得到如下图形：

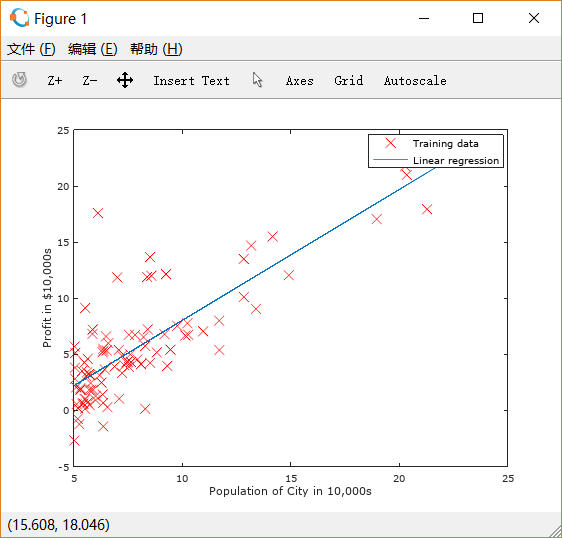
再对population = 35000 和 70000的情况进行估计，输出这两种情况下的估计值：

1.3 Visualizing $J(\theta)$

脚本文件ex1.m提供了对 $J(\theta)$ 可视化的部分。

fprintf('Visualizing J(theta_0, theta_1) ...\n')
% Grid over which we will calculate J
theta0_vals = linspace(-10, 10, 100);
theta1_vals = linspace(-1, 4, 100);

函数 linspace（BASE,LIMIT,N=100) 返回一个从BASE到LIMIT的等间距分布的行向量；如果BASE和LIMIT是列向量的话，返回一个矩阵。不输入N的时候默认为100。

% initialize J_vals to a matrix of 0 s
J_vals = zeros(length(theta0_vals), length(theta1_vals));
% Fill out J_vals
for i = 1:length(theta0_vals)
    for j = 1:length(theta1_vals)
      t = [theta0_vals(i); theta1_vals(j)];
      J_vals(i,j) = computeCost(X, y, t);
    end
end

对 $\theta_0$ 和 $\theta_1$ 平面上的点求出其代价函数值。
绘制曲面图：

% Because of the way meshgrids work in the surf command, we need to
% transpose J_vals before calling surf, or else the axes will be flipped
J_vals = J_vals';
% Surface plot
figure;
surf(theta0_vals, theta1_vals, J_vals)
xlabel('\theta_0'); ylabel('\theta_1');

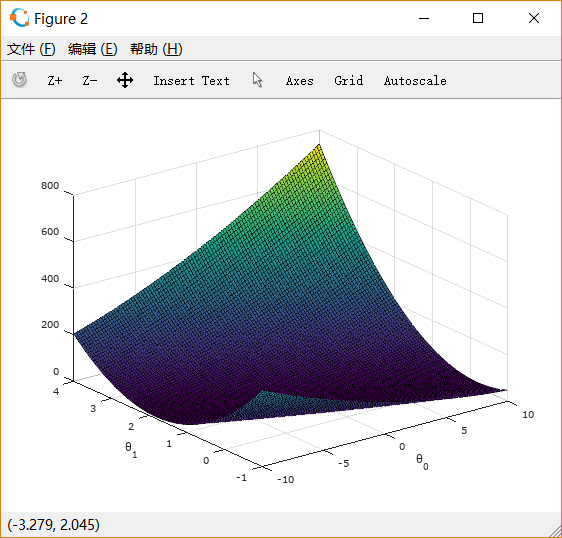
绘制等值线图：

% Contour plot
figure;
% Plot J_vals as 15 contours spaced logarithmically between 0.01 and 100
contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 3, 20))
xlabel('\theta_0'); ylabel('\theta_1');
hold on;
plot(theta(1), theta(2), 'rx', 'MarkerSize', 10, 'LineWidth', 2);

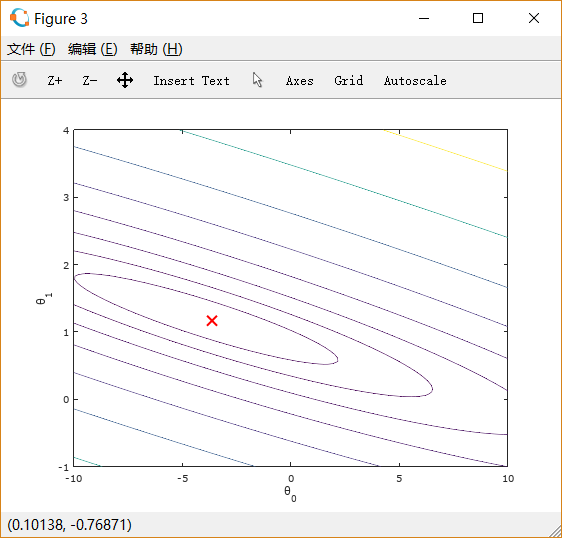
从图中可以看出最小值所在的位置。

2. Linear regression with multiple variables

这一次需要处理多变量的线性回归。比如预测房价，需要考虑的因素可能就包括房子的大小、卧室的数量。
在文件ex1data2.txt中有多变量的 training example。 如下图所示：

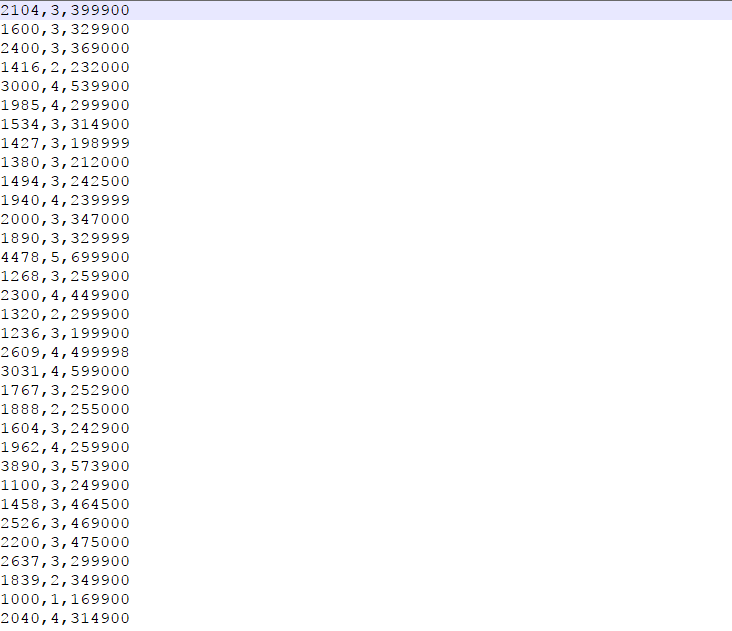
共有三列，第一列是房子面积（单位：平方英尺），第二列是卧室数量，第三列是房价。

2.1 Feature normalization

脚本文件ex1_multi中首先展示部分数据：

%% Load Data 
data = load('ex1data2.txt');
X = data(:, 1:2);
y = data(:, 3);
m = length(y);
% Print out some data points
fprintf('First 10 examples from the dataset: \n');
fprintf(' x = [%.0f %.0f], y = %.0f \n', [X(1:10,:) y(1:10,:)]');
fprintf('Program paused. Press enter to continue.\n');
pause;

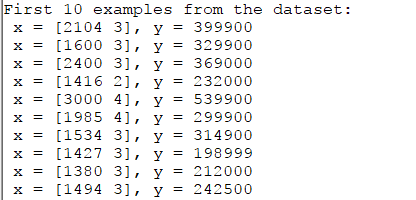
通过观察数据可以发现，第一列数据大小比第二列数据高三个数量级，需要进行标准化（Normalization ）
标准化包括如下步骤：
* 减去平均值
* 除以标准差（因为大部分数据会落在平均值$\pm$标准差的范围内），也可以直接选择用max-min来代替

代码如下：

function [X_norm, mu, sigma] = featureNormalize(X)
%FEATURENORMALIZE Normalizes the features in X 
%   FEATURENORMALIZE(X) returns a normalized version of X where
%   the mean value of each feature is 0 and the standard deviation
%   is 1. This is often a good preprocessing step to do when
%   working with learning algorithms.
% You need to set these values correctly
X_norm = X;
mu = zeros(1, size(X, 2));
sigma = zeros(1, size(X, 2));
% ====================== YOUR CODE HERE ======================
% Instructions: First, for each feature dimension, compute the mean
%               of the feature and subtract it from the dataset,
%               storing the mean value in mu. Next, compute the 
%               standard deviation of each feature and divide
%               each feature by it's standard deviation, storing
%               the standard deviation in sigma. 
%
%               Note that X is a matrix where each column is a 
%               feature and each row is an example. You need 
%               to perform the normalization separately for 
%               each feature. 
%
% Hint: You might find the 'mean' and 'std' functions useful.
% 
mu = mean(X);
sigma = std(X);
for i = 1:size(X,1)
   X_norm(i,:) = (X(i,:)-mu)./sigma;
end;
% ============================================================
end

mean 和 std 分别用来计算向量的平均值和标准差，如果是对象是矩阵的话，默认计算每列的平均值和标准差，然后返回一个行向量。

2.2 Gradient descent

这一部分（包括梯度下降和代价函数），我们在单变量的时候处理的时候已经可以用于多变量了。略去。
值得一提的是，在计算代价函数的时候，用如下方法计算是很有效的：

2.2.1 Selecting learning rates

可以通过修改ex1_multi.m中的learning rate来直观感受其作用。
其中有如下代码：

% Init Theta and Run Gradient Descent 
theta = zeros(3, 1);
[theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters);
% Plot the convergence graph
figure;
plot(1:numel(J_history), J_history, '-b', 'LineWidth', 2);
xlabel('Number of iterations');
ylabel('Cost J');
% Display gradient descent's result
fprintf('Theta computed from gradient descent: \n');
fprintf(' %f \n', theta);
fprintf('\n');

这段代码的功能是画出 $J(\theta)$ 随迭代次数的变化情况。
numel函数返回对象的元素个数。
J_history内存储了每次迭代后的代价函数值。在gradientDescentMulti.m中，我们每一次循环中有这样的步骤来计算J_history：

    % Save the cost J in every iteration    
    J_history(iter) = computeCostMulti(X, y, theta);

设置learning rate $\alpha$ 为 0.01，0.03，0.1，1，1.5 画出的图像依次如下所示：

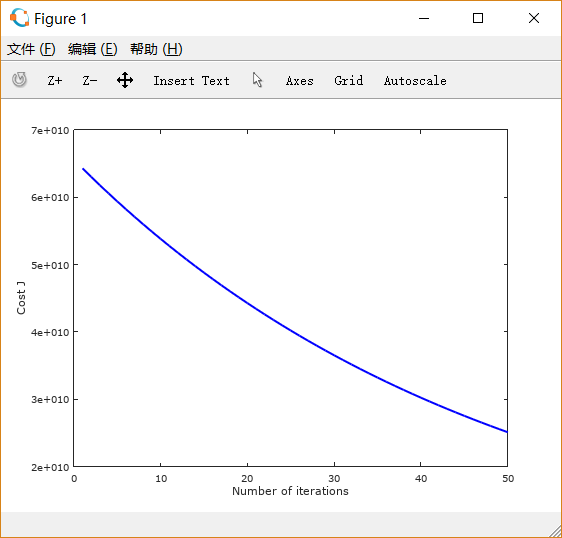
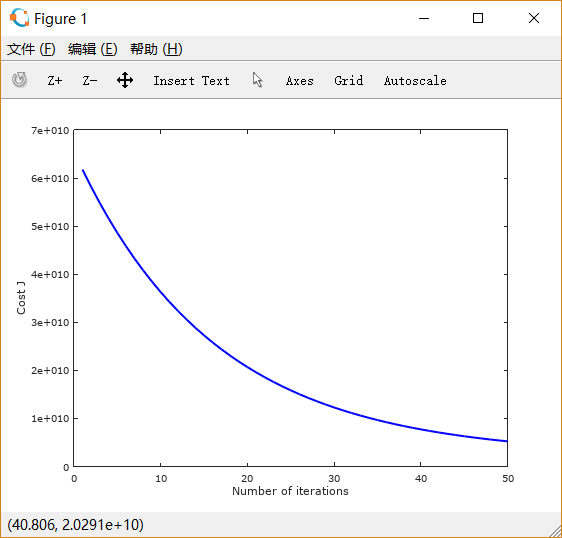
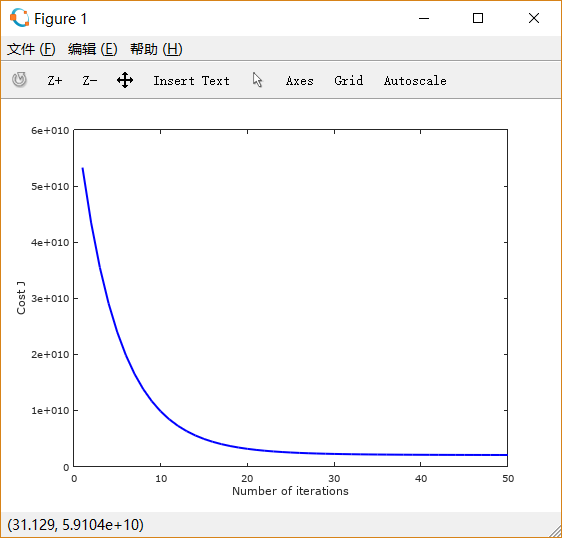
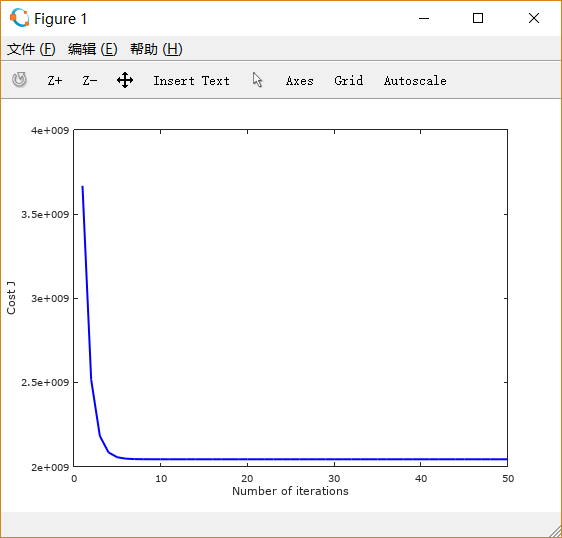
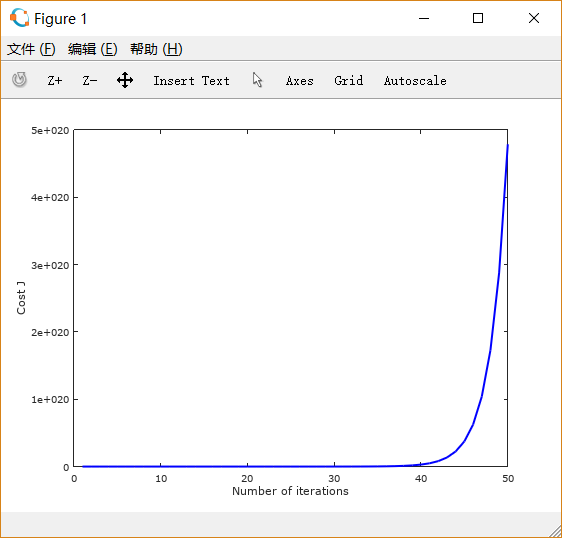
可以注意到，起初 $\alpha$ 设置得很小的时候，下降非常缓慢；$\alpha$ 适当增大之后，下降速度变快；而 $\alpha$ 过大时，图线不降反升。

用梯度下降法在ex1_multi中计算1650平方英尺，3间卧室的房子的价格：

testify = [1,1650, 3];
price = (testify - [0 mu]) ./ [1 sigma] * theta;

需要记得，在使用时要先进行normalization。
输出的结果是：

2.3 Normal equations

$\theta = (X^TX)^{-1}X^T\vec {y}$

代码相当简单：

function [theta] = normalEqn(X, y)
%NORMALEQN Computes the closed-form solution to linear regression 
%   NORMALEQN(X,y) computes the closed-form solution to linear 
%   regression using the normal equations.
theta = zeros(size(X, 2), 1);
% ====================== YOUR CODE HERE ======================
% Instructions: Complete the code to compute the closed form solution
%               to linear regression and put the result in theta.
%
% ---------------------- Sample Solution ----------------------
theta = pinv(X' * X) * X' * y;
% -------------------------------------------------------------
% ============================================================
end

用normal Equation在ex1_multi中计算1650平方英尺，3间卧室的房子的价格：

price = testify * theta;

normal equation 不需要进行normalization。
输出的结果是：

与之前用梯度下降法求出的结果吻合得相当精确。