离散数学第九章 关系（一）

离散数学 关系

part 1. 相关概念

1. 用两个相关元素构成的有序对来表达两个集合元素之间的关系。由有序对组成的集合就叫做二元关系。
2. $A$ 和 $B$ 是集合，一个从 $A$ 到 $B$ 的二元关系是 $A\times B$ 的子集。
3. $aRb\equiv (a,b)\in R, a\not Rb \equiv (a,b) \not \in R$
4. $(a,b) \in R$ 时，$a$ 与 $b$ 有关系 $R$。
5. 函数作为关系： $R$ 是 $A$ 到 $B$ 的关系, 满足：$A$ 中每个元素恰好是 $R$ 中一个有序对的第一元素, $R$ 就可以定义一个函数的图示。（即对 $A$ 中每个元素 $a$ 可指定唯一的 $b \in B$, 使得$(a,b) \in R$。）
6. 集合 $A$ 上的关系是从 $A$ 到 $A$ 的关系。

part 2. 性质

1. 关系的性质：自反性, 对称性， 反对称性，非对称性, 传递性。
   
   • 自反性：$\forall a \in R , 都有(a,a) \in R$，那么定义在 $A$ 上的关系$R$成为自反的(reflexive).
   • 对称性： $\forall a,b \in A, 只要(a,b) \in R, 就有 (b,a) \in R$,则称定义在集合 $A$ 上的关系 $R$ 为对称的(symmetric).
   • 反对称性： $\forall a,b \in A, 若(a,b) \in R 且 (b,a) \in R, 一定有 a=b$,则称定义在$A$上的关系 $R$ 为反对称的(antisymmetric).
   • 非对称性：$\forall a,b \in A, 若(a,b) \in R, 一定有 (b,a) \not \in R$,则称定义在集合 $A$ 上的关系 $R$ 是非对称的(asymmetric).
   • 传递性：$对\forall a,b,c \in A, (a,b) \in R, 且 (b,c) \in R, 则(a,c) \in R$,则称定义在集合 $A$ 上的关系 $R$ 是 传递的(transitive).

用图[1]来表示：

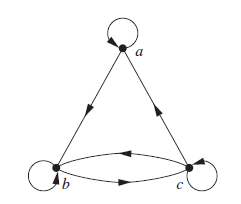
      自反

      对称

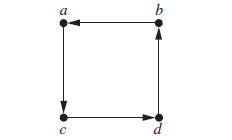
   传递+非对称+反对称

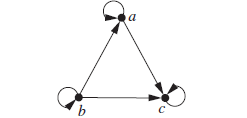
   自反+传递+反对称

2. 关系的组合：$R$ 是从 $A$ 到 $B$的关系， $S$ 是从 $B$ 到 $C$ 的关系。$R$ 与 $S$ 的合成是由有序对$(a,c)$ 构成的关系，其中 $a \in A, c \in C$，且存在$b \in B$，使得$(a,b) \in R, (b,c) \in S$。用 $S \circ R$ 表示。
3. 自身的合成：$R$ 的 $n$ 次幂 $R^{n}$ $(n = 1,2,3...)$递归定义为：
  $R^{1}=R$ 和 $R^{n+1}=R^{n} \circ R$
4. 一个定理：集合 $A$ 上的关系 $R$ 是传递的 $\Leftrightarrow$ 对$n = 1,2,3,...$有 $R^{n} \subseteq R$ .

part 3. 表示方法

1. 用矩阵表示关系：
   $m_{ij}=\begin{cases} 1 \ \ \ \ \left( a_{i},b_{i}\right) \in R\\ 0 \ \ \ \ \left( a_{i},b_{i}\right) \not\in R\end{cases}$
   
   • 自反： 对于$i = 1,2,3,...,n, m_{ij} = 1$.如下所示：
     $$\begin{bmatrix} 1 & & & & & & \\ & 1 & & & & & \\ & & 1 & & & & \\ & & & . & & & \\ & & & & . & & \\ & & & & & 1 & \\ & & & & & & 1 \\ & & & & & & & \end{bmatrix}$$
   • 对称：只要 $m_{ij} = 1$,就有 $m_{ji} = 1$，也就意味着，只要 $m_{ij} = 0$,就有 $m_{ji} = 0$。
     亦即，$M_{R} = (M_{R})^{T}$
   • 反对称：当$i \not = j$ 时, $m_{ij} = 0$或者 $m_{ji} = 0$(也就是说二者不能同时为 $1$）。
     $i = j$ 时 $m_{ij} = 0$ 或 $1$ 均可。
     
   • 非对称：非对称和反对称的区别就是主对角线上不能为 $1$.
   • 关系的合成直接用矩阵的布尔积计算即可，即：
     $M_{S \circ R} = M_{S} \odot M_{R}$
2. 用图的方式表示
   
   • 有向图：由顶点[2]（或结点[3]）集 $V$ 和边[4](或弧[5]集 $E$ 组成。
   • 自反：图示见上。有向图每个顶点都有环(loop)。
   • 对称：图示见上。有向图不同顶点之间的每一条边都存在一条方向相反的边。
   • 反对称：图示见上。有向图两个不同顶点之间不存在两条方向相反的边。（可能存在一条边或没有边）
   • 非对称：图示见上。在反对称条件的基础上，每个顶点都不能有环。