Final Project: Random systems:"random walks","random walks and diffusion" and "diffusion,entropy,and the arrow of time"

一.摘要

1.①.Routine rwalk for simulating one-dimensional random walks and the of x($\Delta{x}$) with $P_{left}=P_{right}=0.5$;②.the value of $\Delta{x}$ with $P_{left}=0.25,P_{right}=0.75$ ;

2.①.The average of the displacement after n steps $<x^2>$ with $P_{left}=P_{right}=0.5$;②.the value of $<x^2>$ with $P_{left}=0.25,P_{right}=0.75$ ;

3.Time evolution calculated from the diffusion equation in one dimension at different values of t;

4.Random-walk simulation of diffusion of cream in coffee and the value of $<r^2>$ in two dimensions.

二.背景介绍

1.$x_n=\sum_{i=0}^n s_i,\Delta{x}=x_1-x,(1)$when $P_{left}=P_{right}=0.5$,we can get a random number r=rnd between 0 and 1;If r<0.5,update x to x+1,otherwise to x-1;

2.Firstly,initialize an array $<x^2=0>$ for i from 1 to n;then accumulate the squared displacement:$<x^2>=<x^2>+x^2,(2)$;lastly,we can get the mean squared displacement:$<x^2>=<x^2>/m,(3)$ for i from 1 to n.

3.The total probability to arrive at x=i is:P(i,n)=1/2[P(i-1,n)+P(i+1,n);the density obeys the equation: $$\frac{\partial \rho}{\partial t}=D*\frac{\partial^2 \rho}{\partial x^2},(4)$$ ;lastly,we can express the density: $$\rho(x,t)=\frac{exp(-\frac{x^2}{2\sigma^2})}{\sigma},(5)$$

4.$x_n=\sum_{i=0}^n s_i,y_n=\sum_{i=0}^n s_i$,for $P_{left}=P_{right}=P_{up}=P_{down}=0.25$,similiarly,we can get a random number r=rnd between 0 and 1;If r<0.25,update x to x+1;elif r<0.5,to x-1;elif r<0.75,update y=y+1;otherwise to y-1.

三.正文

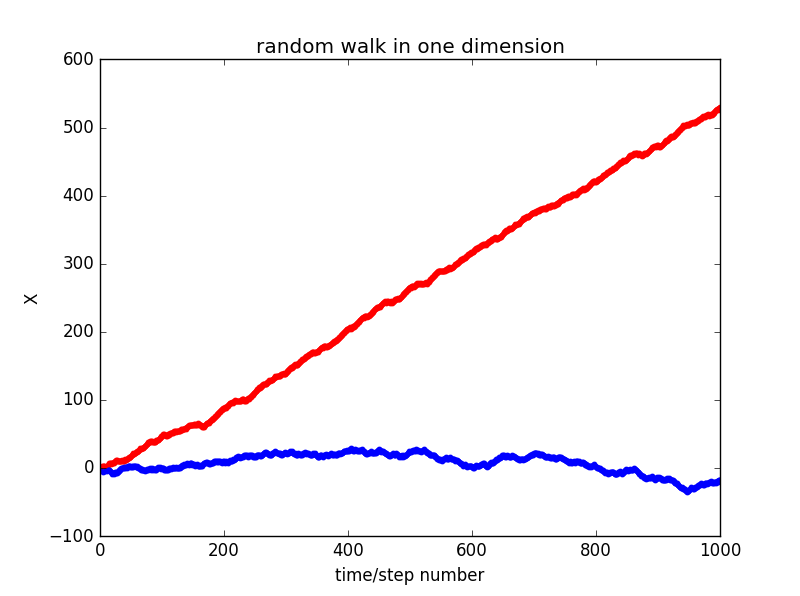
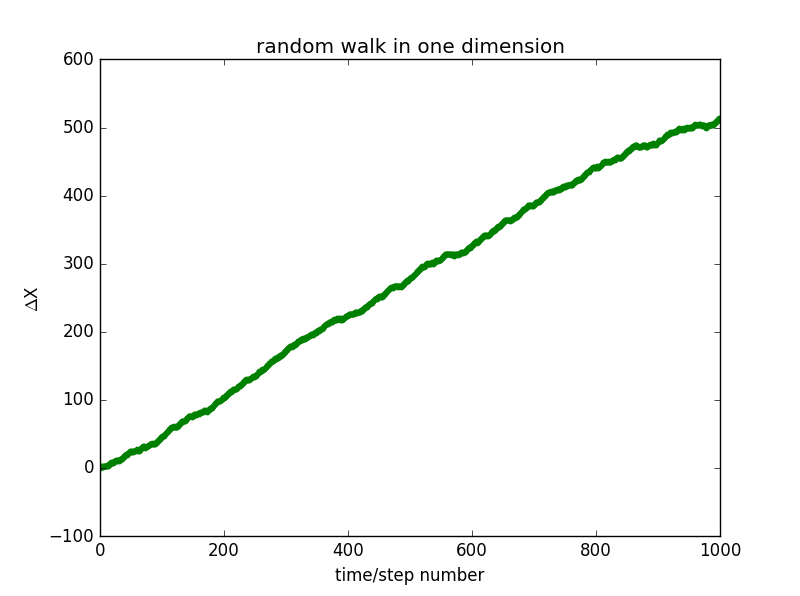
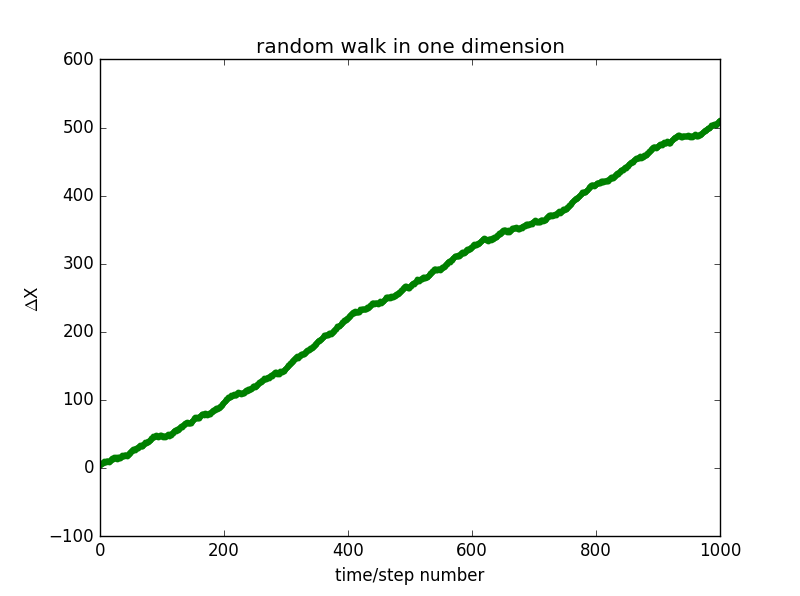
1.①$P_{left}=P_{right}=0.5$,x versus step number and $\Delta{x}$ for two random walks in one dimension:

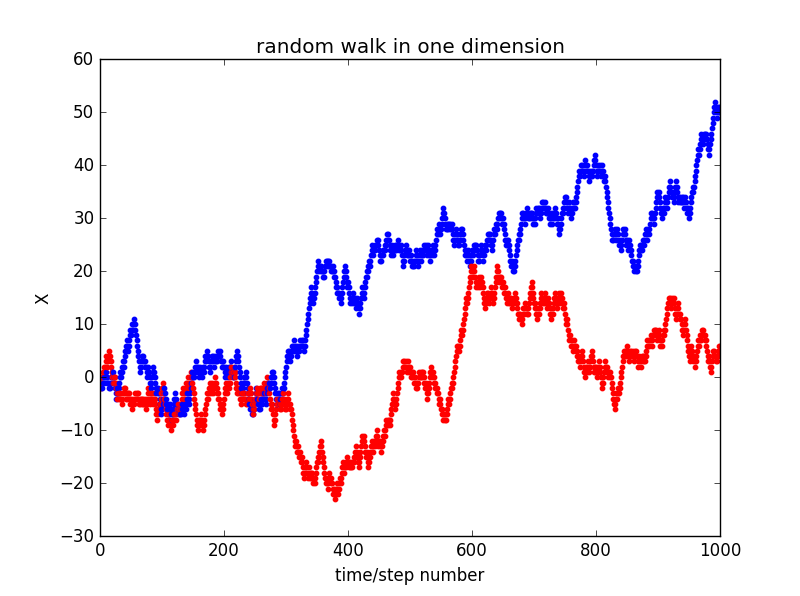
x0=0

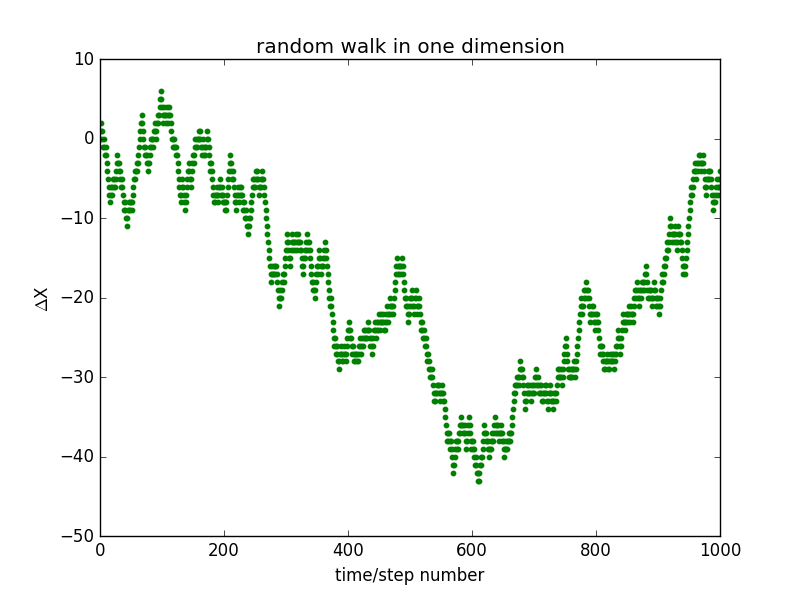
x0=1

import random 
import numpy as np 
import matplotlib.pyplot as plt 
import math 
def randpath(tt): 
    b=[]
    b1=[]
    bb=[] 
    b.append(0)
    b1.append(0)
    bb.append(0) 
    b_=[] 
    b_1=[]
    d=[]
    for i in range(tt): 
        c=random.random() 
        bb.append(i+1) 
        if c<=0.5: 
            b.append(b[-1]+1) 
            b1.append(b1[-1]+1)
        else: 
            b.append(b[-1]-1)
            b1.append(b1[-1]-1)
        d.append(abs(b1[i])-abs(b[i]))
    for j in range(len(b)): 
         b_.append(b[j]) 
    for l in range(len(b1)): 
         b_1.append(b1[l]) 
    return b,b1,bb,b_,b_1 
a,b,b1,c,d=randpath(1000)
for k in range(len(d)): 
    plt.scatter(k,[d[k],],10,color='green')
plt.xlim(0,1000) 
plt.xlabel('time/step number') 
plt.ylabel('$\Delta$X') 
plt.title('random walk in one dimension') 
plt.show() 

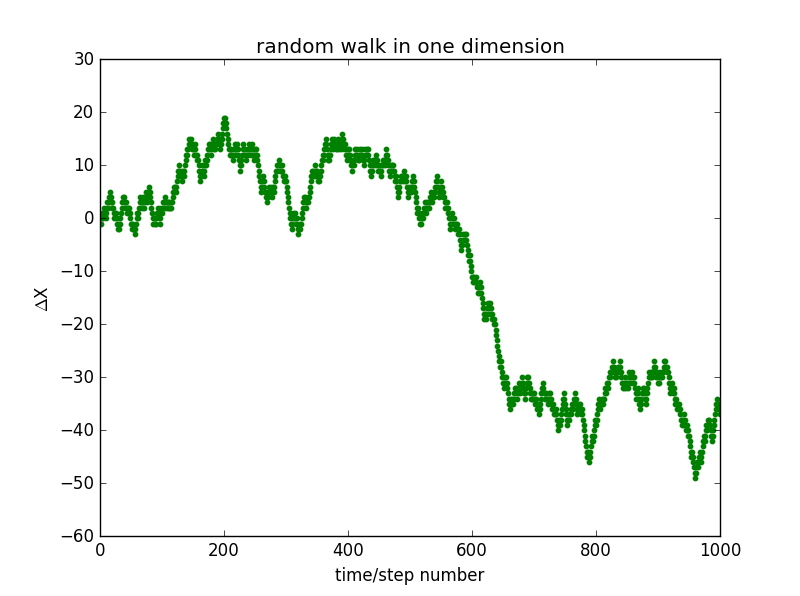
②$P_{left}=0.25,P_{right}=0.75,x_0=0$:

$x_0=1$

$x_0=5$

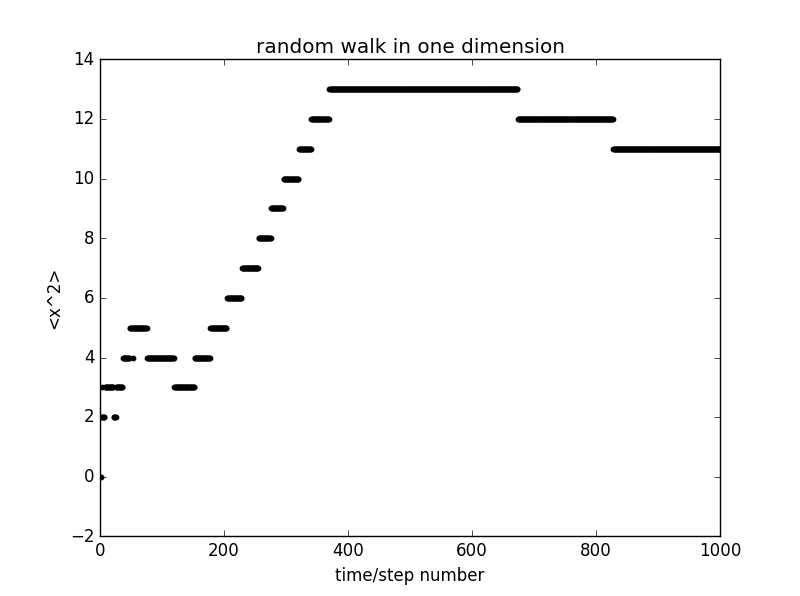
2. ①$P_{left}=P_{right}=0.5$:

import random 
import numpy as np 
import matplotlib.pyplot as plt 
import math 
def randpath(tt): 
    b=[] 
    bb=[]
    a=[]
    a_=[]
    b.append(0) 
    bb.append(0) 
    a.append(0)
    a_.append(0)
    b2=[] 
    for i in range(tt): 
        c=random.random() 
        bb.append(i+1) 
        if c<0.75: 
            b.append(b[-1]+1) 
        else: 
            b.append(b[-1]-1)
        a.append(abs(a[i])+abs((b[i])^2))
        if i>0:
            a_.append(a[i]/i)
        else:
            a_.append(0)
    for j in range(len(b)): 
         b2.append(b[j]) 
    return a,a_,b,bb,b2 
a,a_,b,bb,c=randpath(1000)  
for k in range(len(b)): 
    plt.scatter(k,[a_[k],],10,color='purple')
plt.xlim(0,1000) 
plt.xlabel('time/step number') 
plt.ylabel('<x^2>') 
plt.title('random walk in one dimension') 
plt.show() 

②$P_{left}=0.25,P_{right}=0.75$:

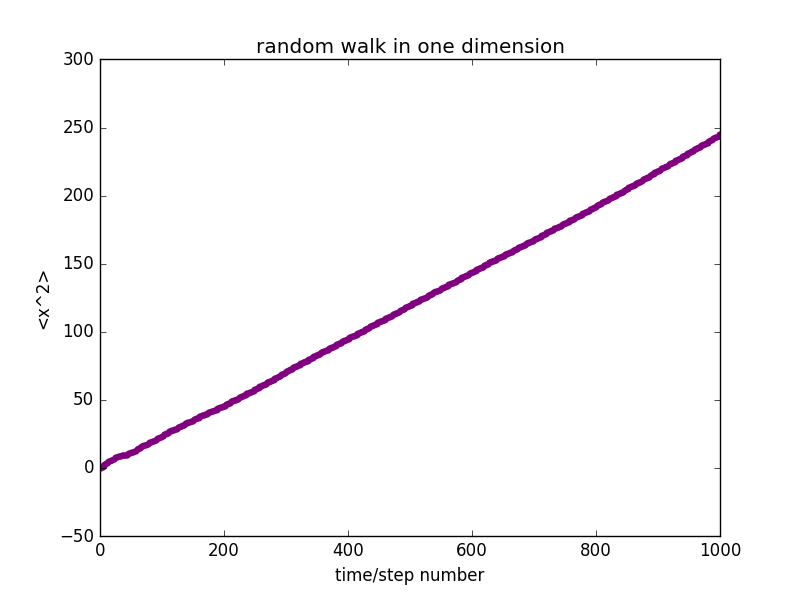
3.Diffusion in one dimension with different values of t:

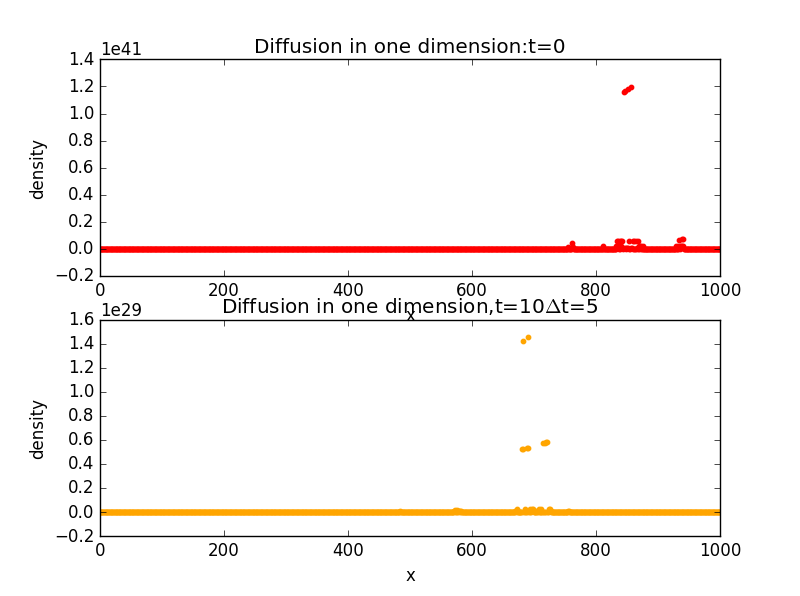
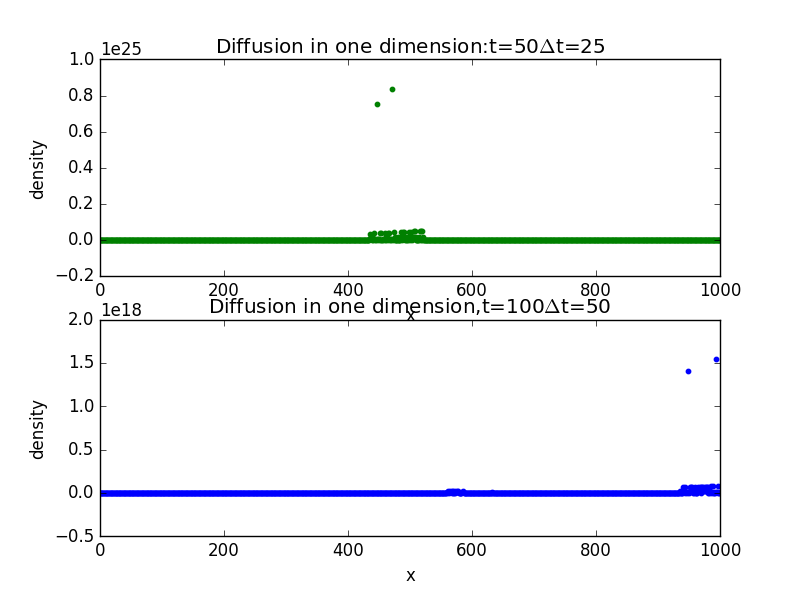
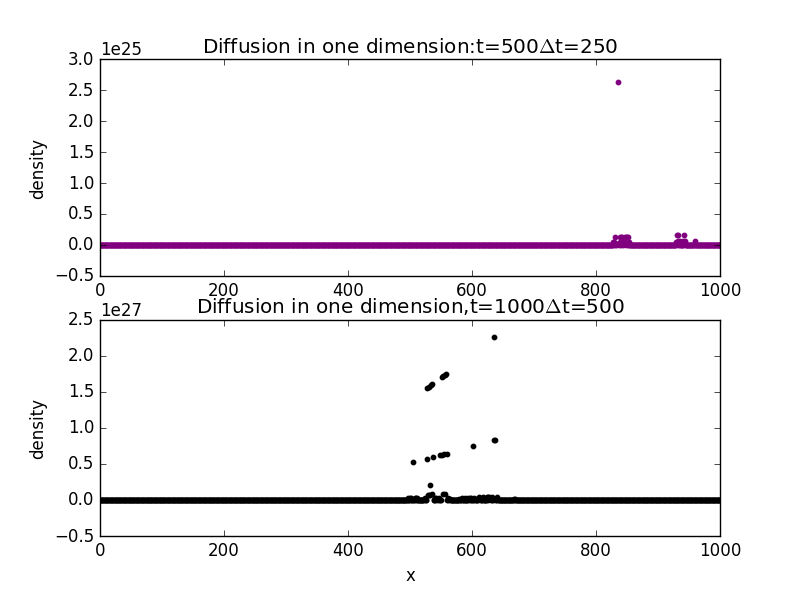
import random 
import numpy as np 
import matplotlib.pyplot as plt 
import math 
def randpath(tt): 
    b=[] 
    bb=[]
    a=[]
    a_=[]
    b.append(0) 
    bb.append(0) 
    a.append(0)
    a_.append(0)
    b2=[] 
    for i in range(tt): 
        c=random.random() 
        bb.append(i+1) 
        if c<=0.5: 
            b.append(b[-1]+1) 
        else: 
            b.append(b[-1]-1)
        a.append(abs(math.exp(abs(-b[i]^2))*abs((4*bb[i])^(-1))))
        if bb[i]>0:
            if a[i]>0:
                a_.append((abs(a[i])*abs((2*bb[i])^(-2))))
            else:
                a_.append(0)
        elif bb[i]<=0:
            a_.append(b[i])
    a_[0]=0 
    a_[-1]=0
    for j in range(len(b)): 
         b2.append(b[j]) 
    return a,a_,b,bb,b2 
plt.subplot(211)
a,a_,b,bb,c=randpath(1000)
bb[-1]=250
for k in range(len(b)): 
    plt.scatter(k,[a_[k],],10,color='purple')
plt.xlim(0,1000)
plt.ylabel('density') 
plt.title('Diffusion in one dimension:t=500$\Delta$t=250') 
plt.subplot(212)
a,a_,b,bb,c=randpath(1000)
bb[-1]=500
for k in range(len(b)): 
    plt.scatter(k,[a_[k],],10,color='black')
plt.xlim(0,1000)
plt.xlabel('x') 
plt.ylabel('density') 
plt.title('Diffusion in one dimension,t=1000$\Delta$t=500') 
plt.show()

4.Cream in coffee with different values of t:

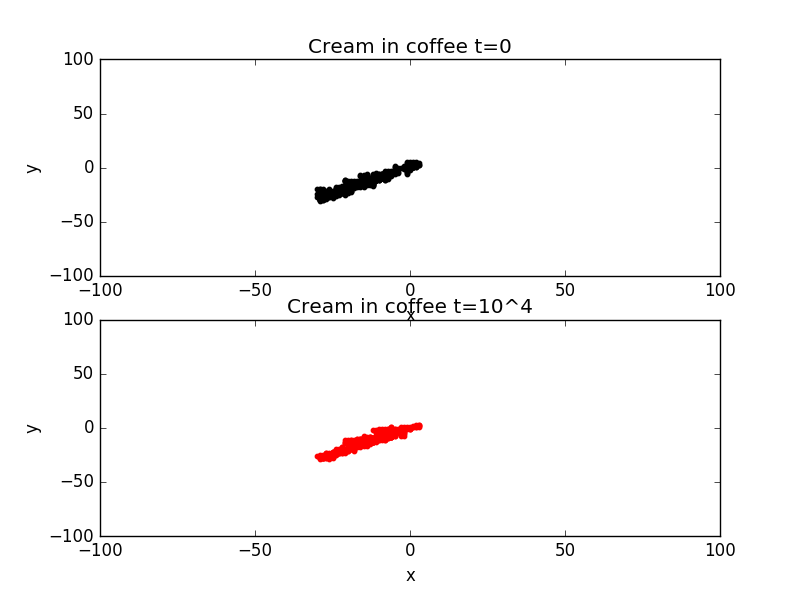
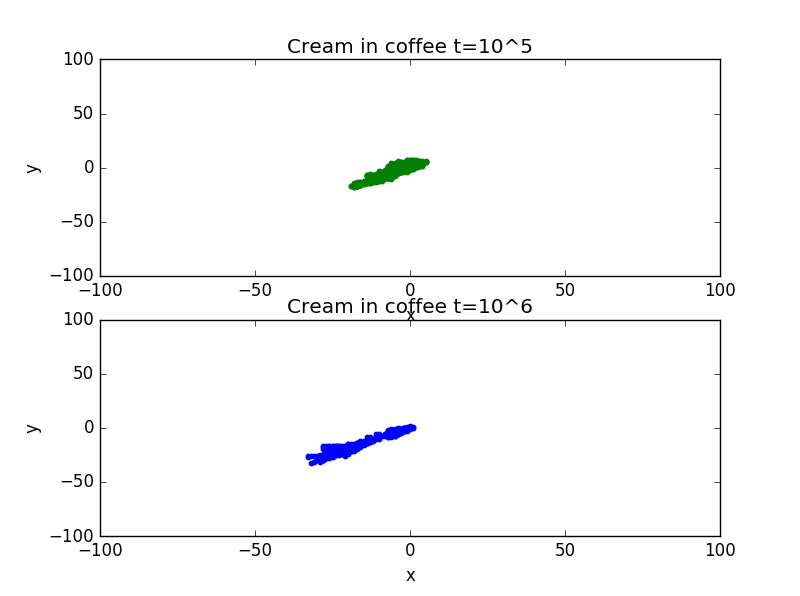
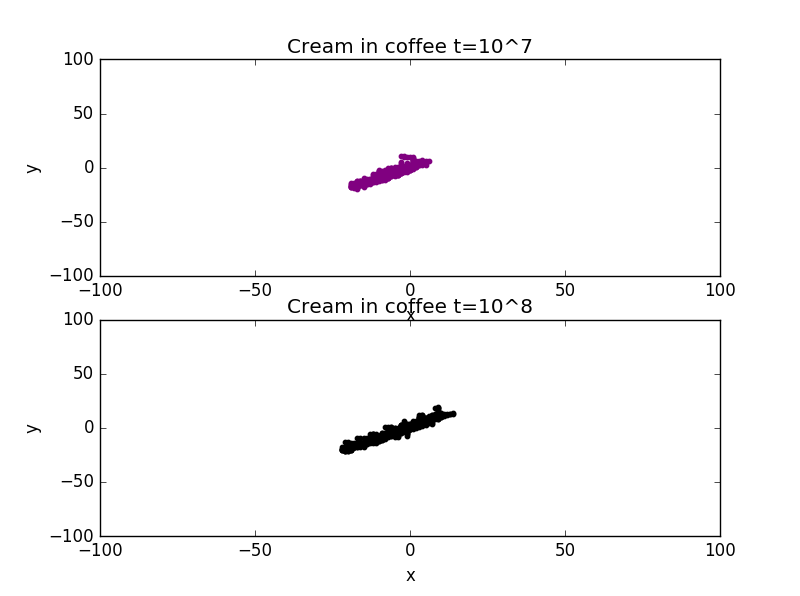
import random 
import numpy as np 
import matplotlib.pyplot as plt 
import math 
def randpath(tt): 
    b=[]
    b1=[]
    bb=[]
    a=[]
    a_=[]
    b.append(0)
    b1.append(0)
    bb.append(0) 
    a.append(0)
    a_.append(0)
    b2=[] 
    for i in range(tt): 
        c=random.random() 
        bb.append(i+1) 
        if c<=0.25: 
            b.append(b[-1]+1)
            b1.append(b[-1])
        elif c<=0.5:
            b.append(b[-1]-1)
            b1.append(b1[-1])
        elif c<=0.75:
            b.append(b[-1])
            b1.append(b1[-1]+1)
        else: 
            b.append(b[-1])
            b1.append(b1[-1]-1)
        a.append(abs(a[i])+abs((b[i])^2)+abs((b1[i])^2))
        if i>0:
            a_.append(a[i]/i)
        else:
            a_.append(0)
    for j in range(len(b)): 
         b2.append(b[j]) 
    return a,a_,b,bb,b1 
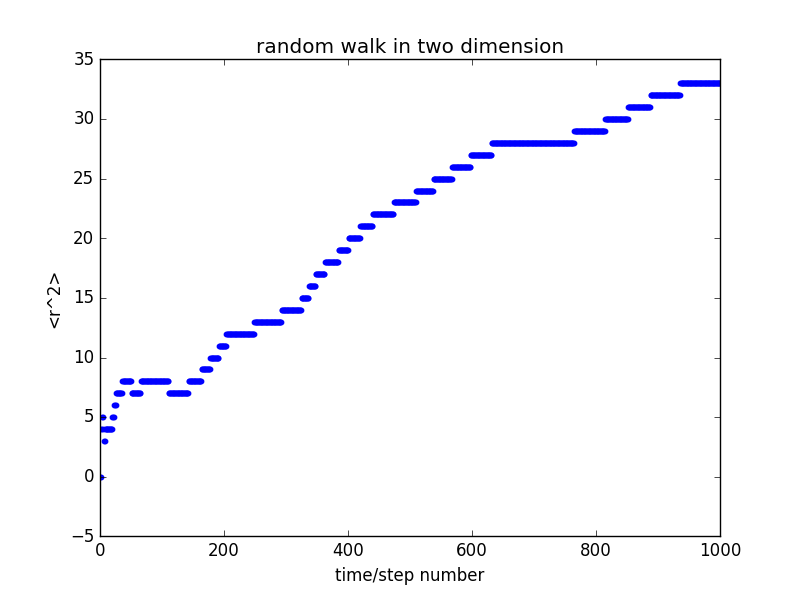
a,a_,b,bb,b1=randpath(1000)  
for k in range(len(b)): 
    plt.scatter([b[k],],[b1[k],],10,color='blue')
plt.xlim(0,1000) 
plt.xlabel('time/step number') 
plt.ylabel('x') 
plt.title('random walk in two dimension') 
plt.show() 

四.结论

1.When the initial displacement $x_0$ is different,the rate of variation of $\Delta{x}$ is different;

2.$<x^2>$ is proportional to time/step number;while,with different values of $P_{left} and P_{right}$,the slope of $<x^2> verus time/number$ is different;

3.The density is almostly distributed at a smaller range of x;

4.In two dimensions $<r^2>$ is also proportional to time/step number;as the time going by,the distribution will change in some degree.