Exercise_10: Chapter 4 Proroblem 4.10&4.11

一.摘要:

Investigate how the precession of the perihelion of a planet's orbit due to general relativity varies as a function of the eccentricity of the orbit.

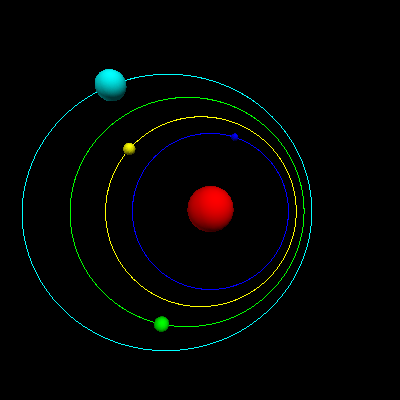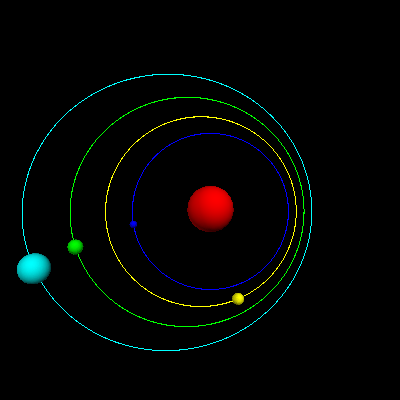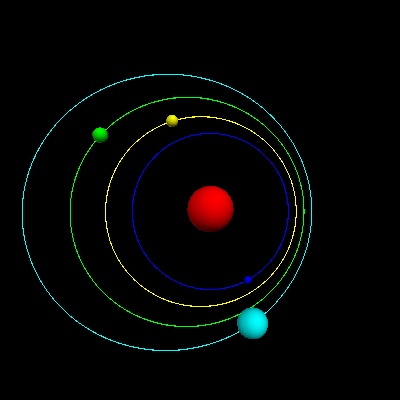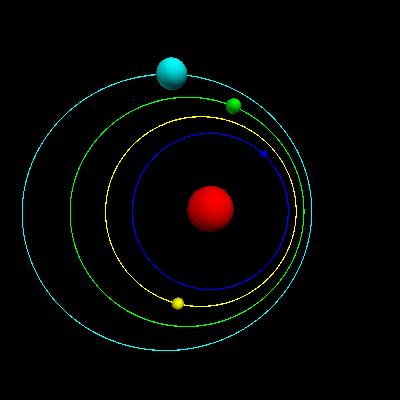
二.背景介绍：

1.The force law predicted by general relativity is $$F_G=\frac{G*M_S*M_M}{r^2}*(1+\frac{\alpha}{r^2}),(10-1)$$

2.From Newton's second law of motion,we have $$\ddot{x}=\frac{F_{G,x}}{M_E},(10-2)$$ $$\ddot{y}=\frac{F_{G,y}}{M_E}$$

3.$F_{G,x}=-F_G*cos{\theta}=-\frac{G*M_S*M_M}{r^3}*(1+\frac{\alpha}{r^2})*(x+ae),(10-3)$$F_{G,y}=-F_G*cos{\theta}=-\frac{G*M_S*M_M}{r^3}*(1+\frac{\alpha}{r^2})*y$

4. $$v_{x,i+1}=v_{x,i}-\frac{4*{\pi}^2}{r_i^3}*(1+\frac{\alpha}{r_i^2})*(x_i+ae)*\Delta{t},(10-4)$$ $$x_{i+1}=x_i+v_{x,i+1}*\Delta{t}$$ $$v_{y,i+1}=v_{y,i}-\frac{4*{\pi}^2}{r_i^3}*(1+\frac{\alpha}{r_i^2})*y_i*\Delta{t}$$ $$y_{i+1}=y_i+v_{y,i+1}*\Delta{t}$$ $$r_i=(x_i^2+y_i^2)^0.5$$

三正文：

1.Simulation of the precession of Mercury with different eccentricity:

from numpy import *
import matplotlib.pyplot as plt
_alpha=0.000000011
class INVERSE(object):
''’
e: ellipticity
m: mass of central star
dt, time : time step size and total time
'''
def init(self, _e=0., _m=4*(pi**2), _dt=0.0001, _time=100):
self.m=_m
self.e=_e
self.x, self.y=[1.],[0.]
self.vx, self.vy=[0],[sqrt(_m)*sqrt((1.-_e)/(1.+_e))]
self.alpha=_alpha
self.dt=_dt
self.time= _time
self.n=int(_time/_dt)
#print self.x[-1],self.y[-1],self.vx[-1],self.vy[-1]
def cal(self): # use Euler-Cromer Method to calculate the trajectory of stars
for i in range(self.n):
self.r=sqrt(self.x[-1]**2+self.y[-1]**2)
self.vx.append(self.vx[-1]+self.dt*(-self.m*(self.x[-1]+self.e)*(1.+self.alpha/self.r**2.)/self.r**3.))
self.vy.append(self.vy[-1]+self.dt*(-self.m*self.y[-1]*(1.+self.alpha/self.r**2.)/self.r**3.))
self.x.append(self.x[-1]+self.vx[-1]*self.dt)
self.y.append(self.y[-1]+self.vy[-1]*self.dt)
def plot_trajectory(self): # plot the trajectory
plt.plot(self.x,self.y,markersize=0.5,label='e= %.2f'%self.e)
plt.plot([self.x[-1]],[self.y[-1]],markersize=8)
plt.plot([0],[0],'or',markersize=20)
def precession_rate(self): # calculate the precession rate
self.x_critical=0
self.y_critical=0
self.t_critical=0
for i in range(len(self.x)-2):
self.r_i=sqrt(self.x[i]**2+self.y[i]**2)
self.r_i1=sqrt(self.x[i+1]**2+self.y[i+1]**2)
self.r_i2=sqrt(self.x[i+2]**2+self.y[i+2]**2)
if self.r_iself.r_i2:
self.x_critical=self.x[i+1]
self.y_critical=self.y[i+1]
self.t_critical=self.dt*(i+1)
break
self.rate = arctan(self.y_critical/self.x_critical)/self.t_critical
return self.rate
# calculate the trajectory of planet with different ellipticity
for i in range(5):
fig=plt.figure(figsize=(10,10))
plt.xlim(-1.2,1.2)
plt.ylim(-4,1.2)
plt.xlabel(r'$x$'+' (AU)',fontsize=18)
plt.ylabel(r'$y$'+' (AU)',fontsize=18)
plt.title(r'$\alpha=0.01$'+' '+'e='+str(i*0.2),fontsize=18)
cmp=INVERSE(0.01,i*0.2)
cmp.cal()
cmp.plot_trajectory()
plt.show()

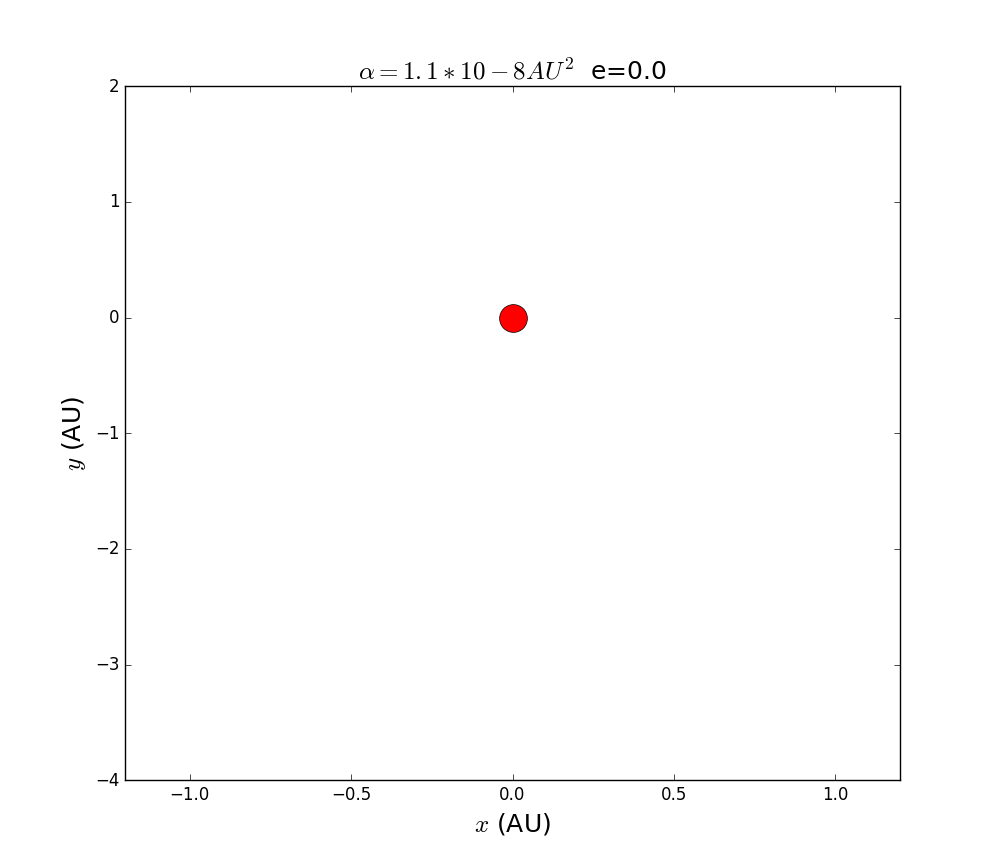
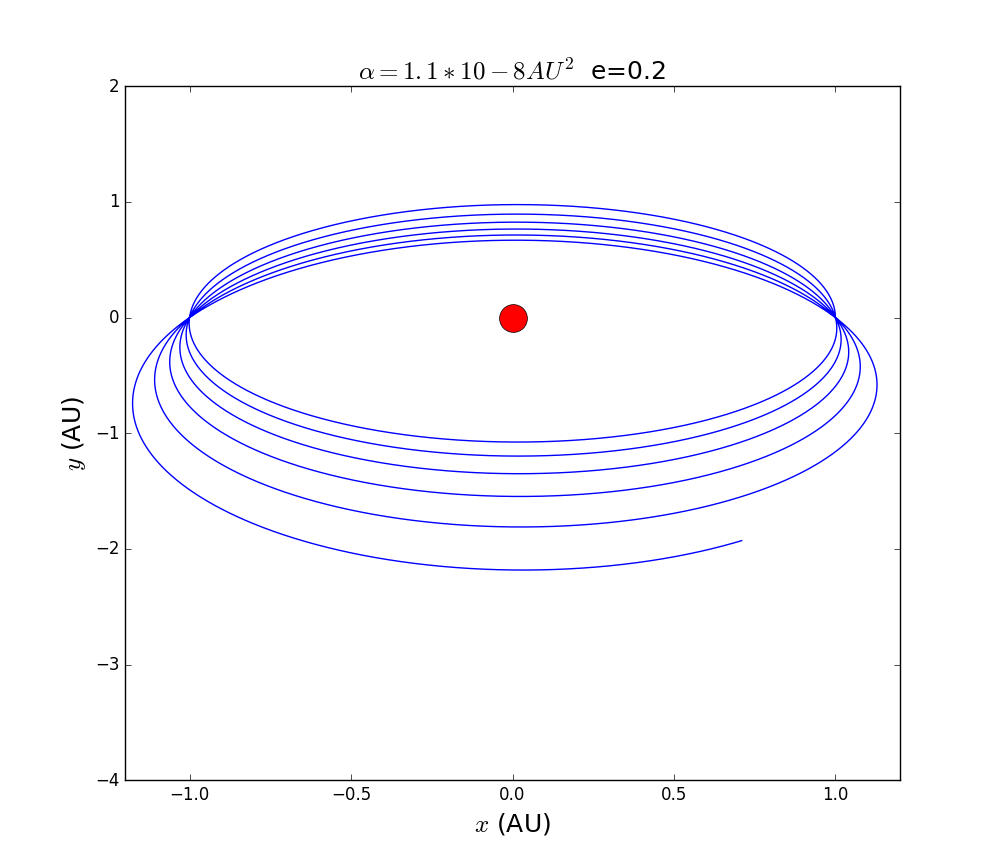
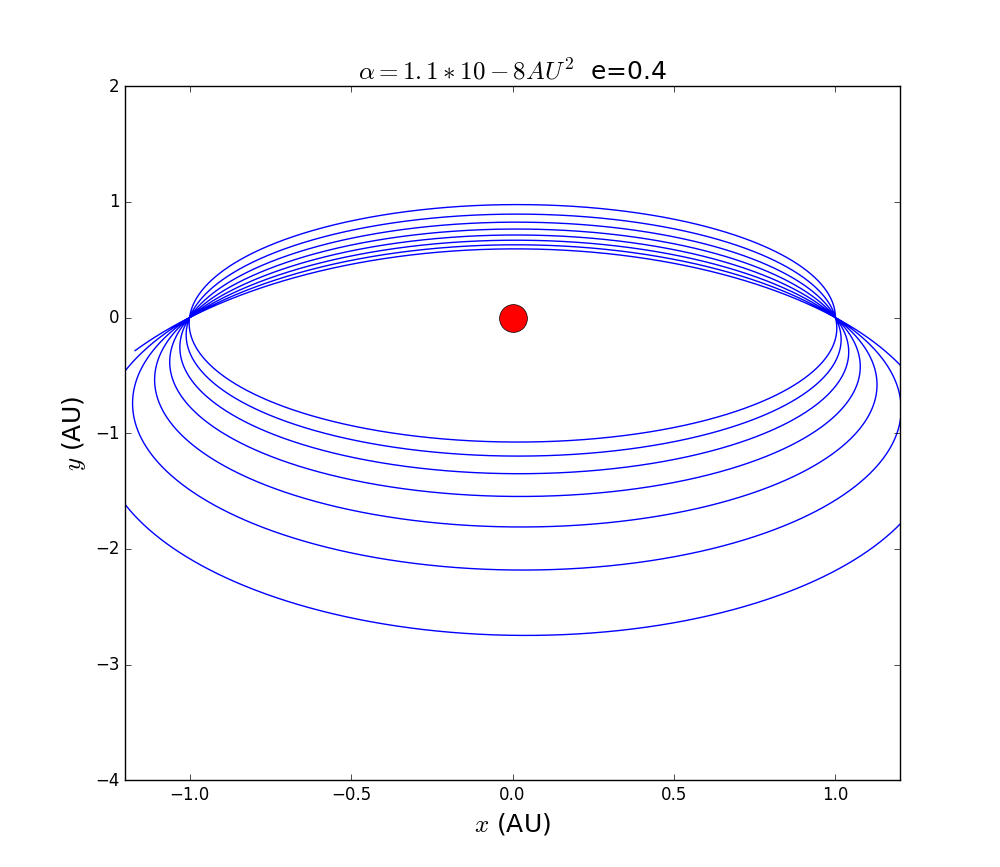
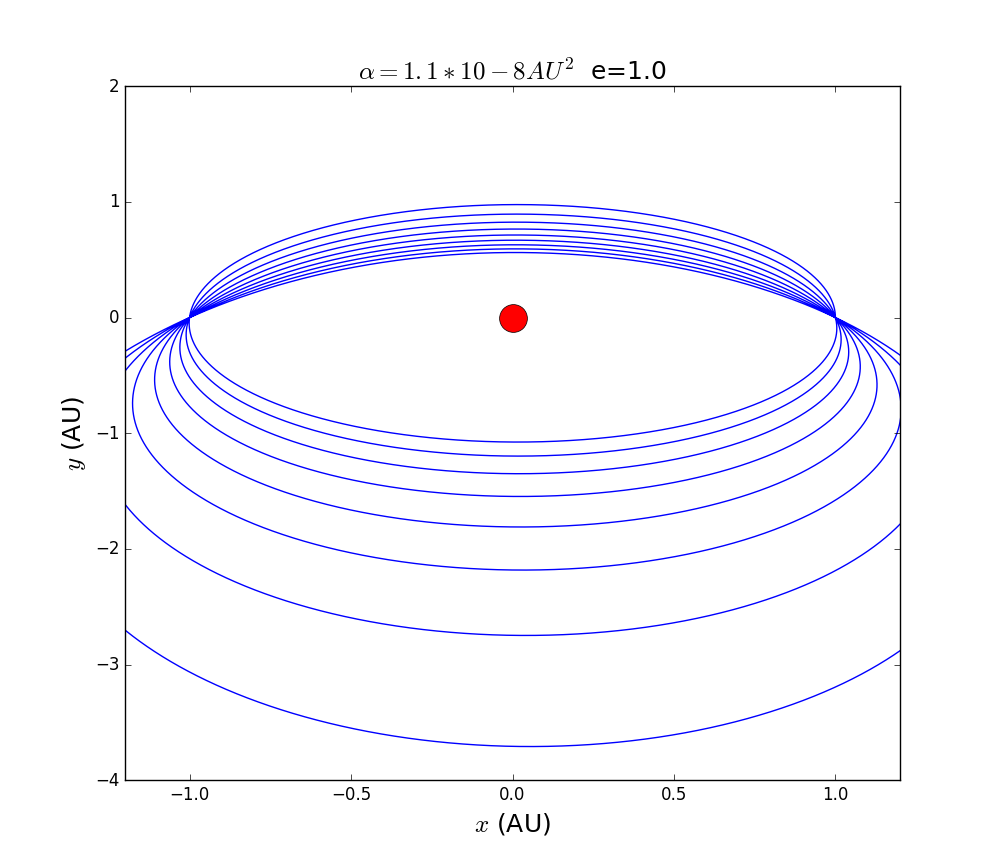
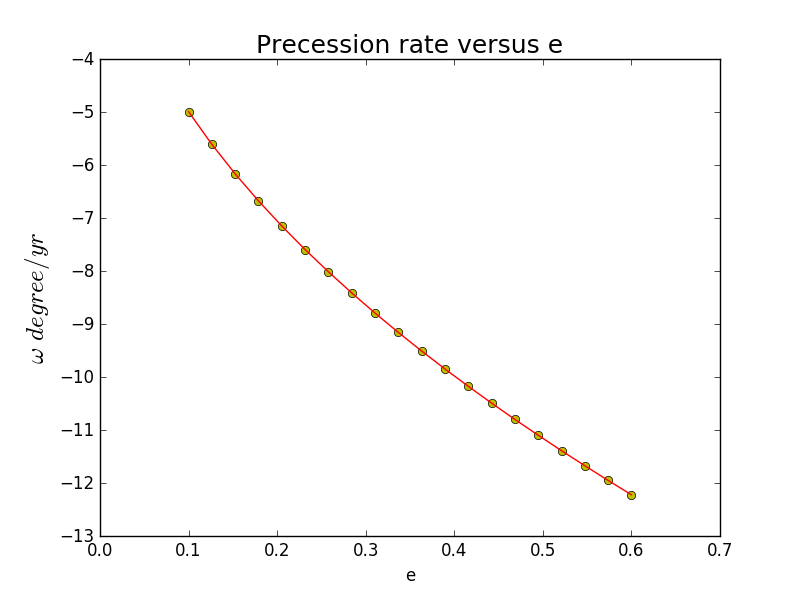
2.Simulation of the precession of Mercury:

e=[]
rate=[]
for i in linspace(0.1,0.6,20):
cmp= INVERSE(0.01,i)
cmp.cal()
e.append(i)
rate.append(180/pi*cmp.precession_rate())
plt.xlim(-0,0.7)
plt.xlabel(r'e')
plt.ylabel(r'$\omega$ '+r'$degree/yr$',fontsize=18)
plt.title(r'Precession rate versus e',fontsize=18)
plt.plot(e,rate,'oy')
plt.plot(e,rate,'-r')
plt.show()

四.结论：由图像'Precession rate versus e'可知，当a=1时，离心率越大，水星进动的角速度越小，即水星进动的角速度与离心率呈反比例。

五.致谢：Grateful to Dingdongdong for reference.