Exercise_11: Chapter 4 problem 4.19 &4.20

一.摘要:

Study the behavior of Hyperion for different initial conditions;Estimate the Lyapunov exponent fron calculation of $\Delta{\theta}$ ;Considering $\Delta{\theta}$ as a discontinuous jump.

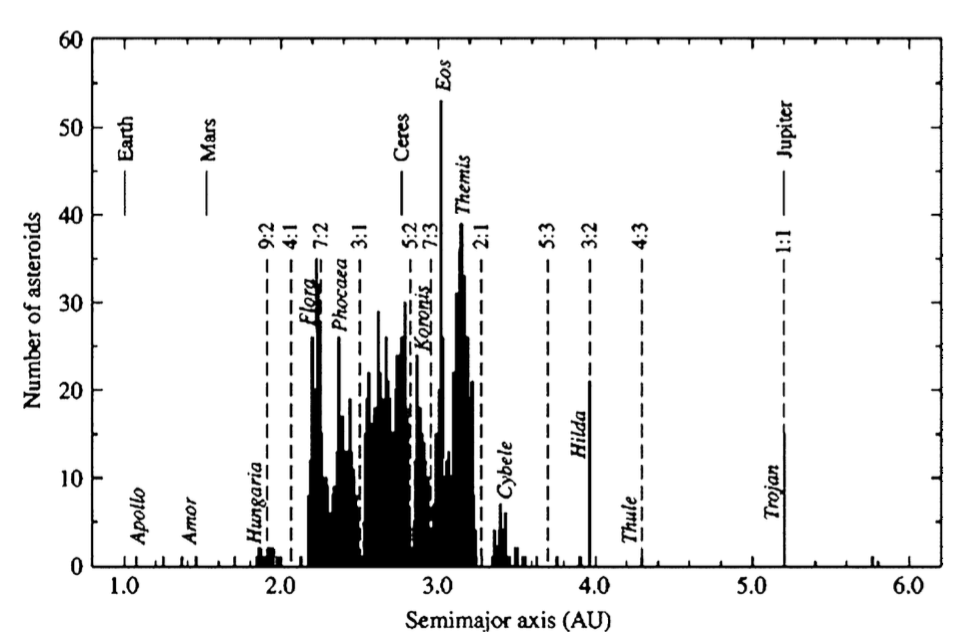
二.背景介绍:

1.The force law predicted by general relativity is $$F_G=\frac{G*M_{Sat}*M_{Hyp}}{r^2},(11-1)$$

2.From Newton's second law of motion,we have $$\ddot{x}=\frac{F_{G,x}}{M_{Hyp}},(11-2)$$ $$\ddot{y}=\frac{F_{G,y}}{M_{Hyp}}$$

3.$F_{G,x}=-F_G*cos{\theta},(11-3)$$F_{G,y}=-F_G*sin{\theta}$

4. $$v_{x,i+1}=v_{x,i}-\frac{4*{\pi}^2*x_i}{r_i^3}*\Delta{t},(10-4)$$ $$x_{i+1}=x_i+v_{x,i+1}*\Delta{t}$$ $$v_{y,i+1}=v_{y,i}-\frac{4*{\pi}^2*y_i}{r_i^3}*\Delta{t}$$ $$y_{i+1}=y_i+v_{y,i+1}*\Delta{t}$$ $$r_i=(x_i^2+y_i^2)^{0.5},$$ $$\omega_{i+1}=\omega_i-\frac{3*GM_{Sat}}{r_i^5}*{x_i*sin{\theta_i}-y_i*cos{\theta_i}}*{x_i*cos{\theta_i}-y_i*sin{\theta_i}}*\Delta{t}$$ $$\theta_{i+1}=\theta_i+\omega_{i+1}*\Delta{t}$$

三.正文:

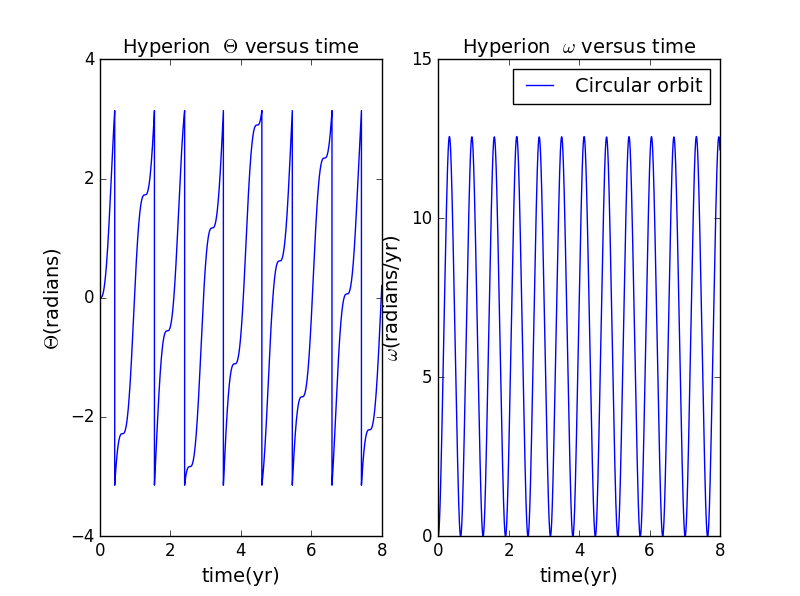
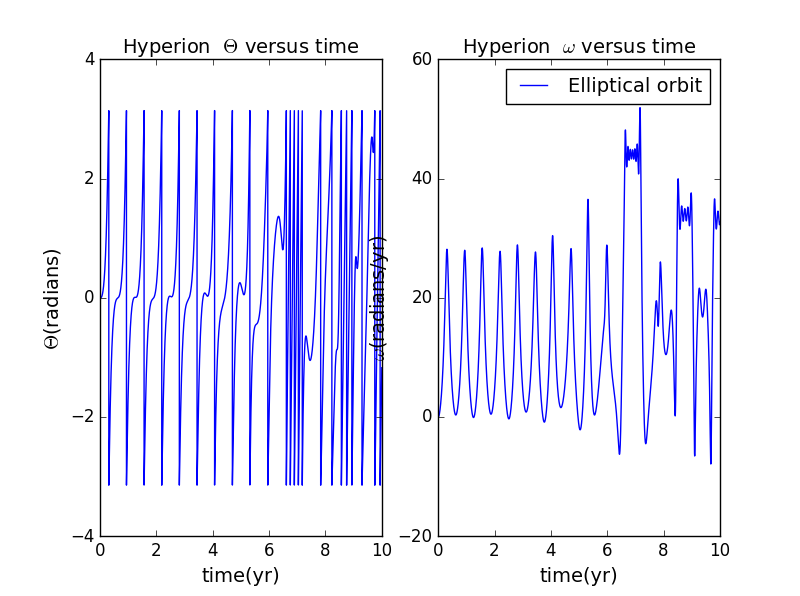
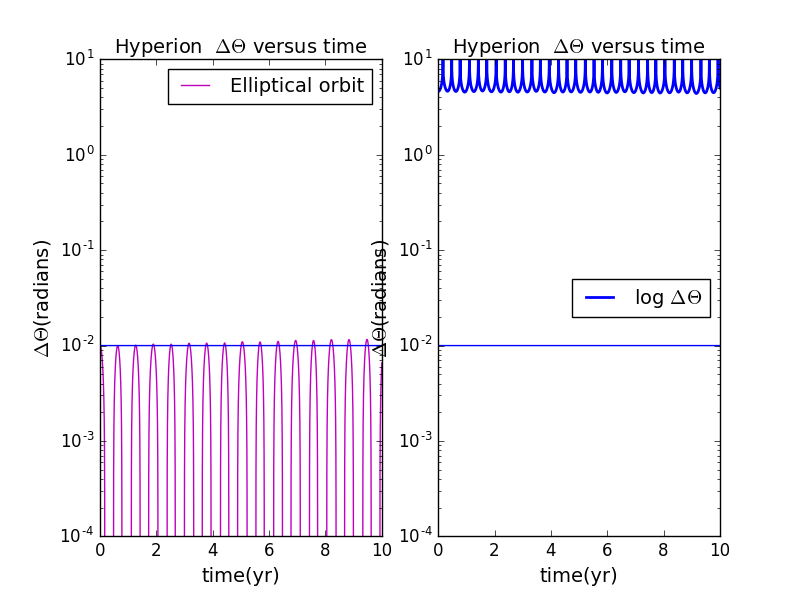
1.The behavior of Hyperion when $\theta$ is restricted to the range of $-\pi$ to $\pi$ for $v_1={\frac{4{\pi}^2(1-e)}{a(1+e)}}^{1/2}=1$,when a=1 and e=0.95;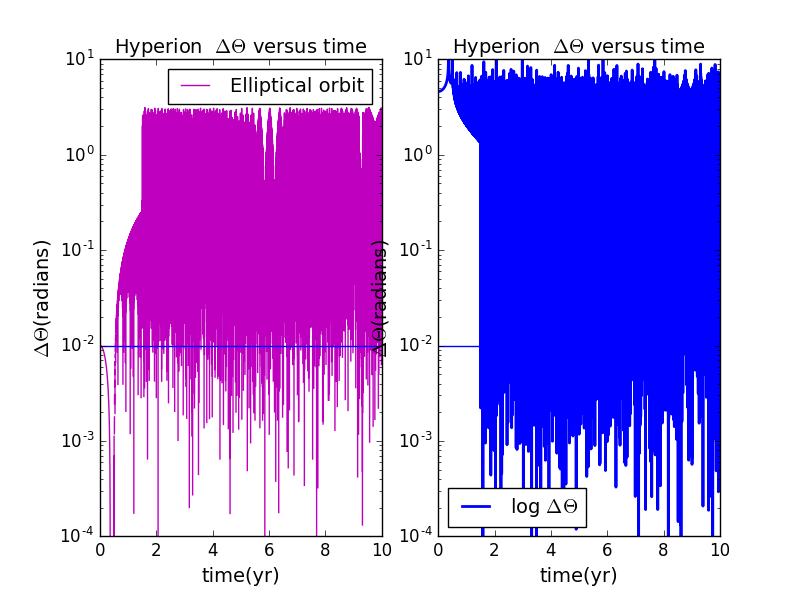

2.when $v_1=2$ and e=0.816:

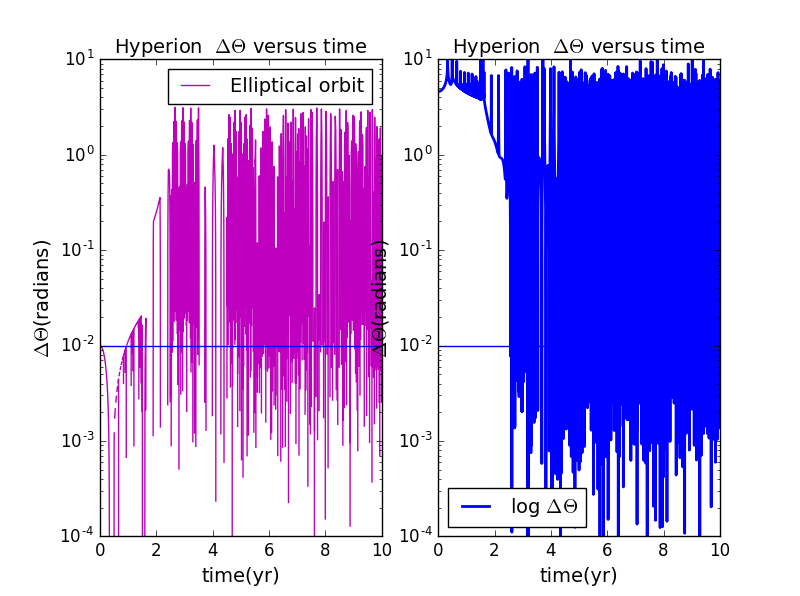
3.when $v_1=3$ and e=0.629:

4.when $v_1=4$ and e=0.423:

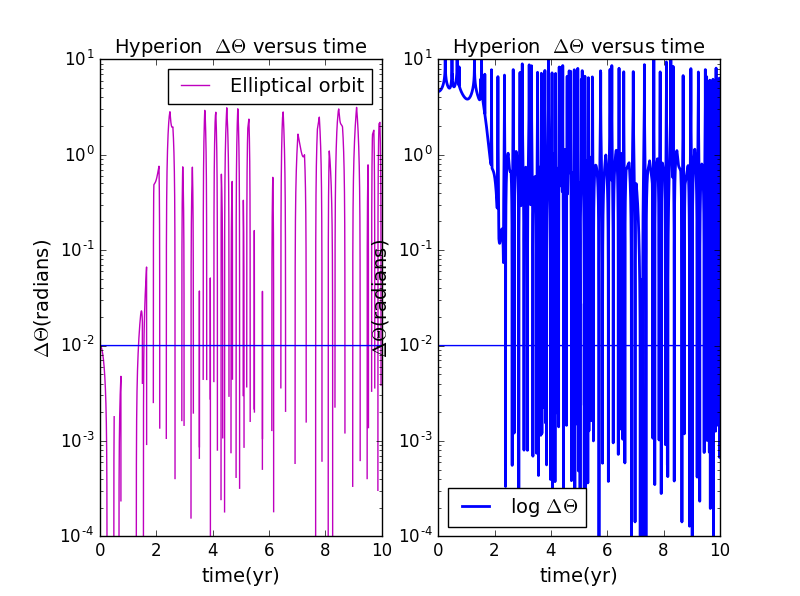
5.when $v_1=5$ and e=0.225:

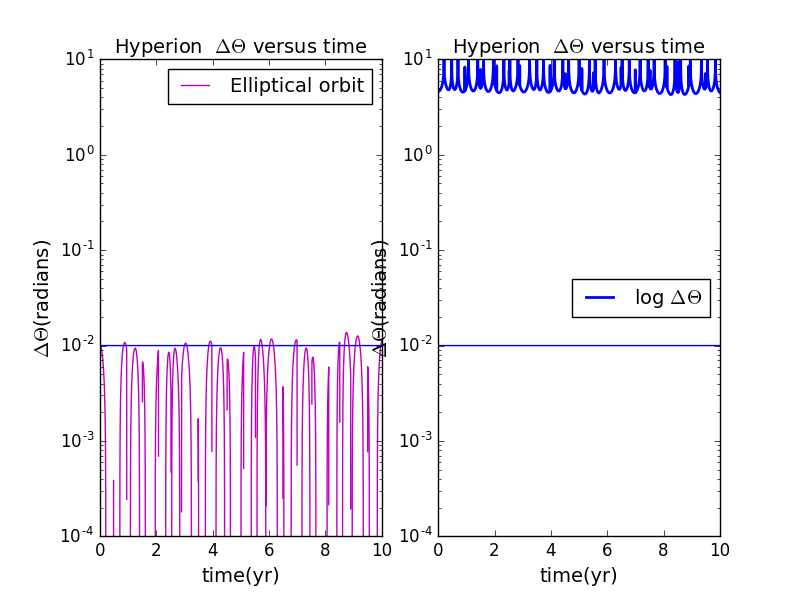
6.when $v_1=6$ and e=0.05:

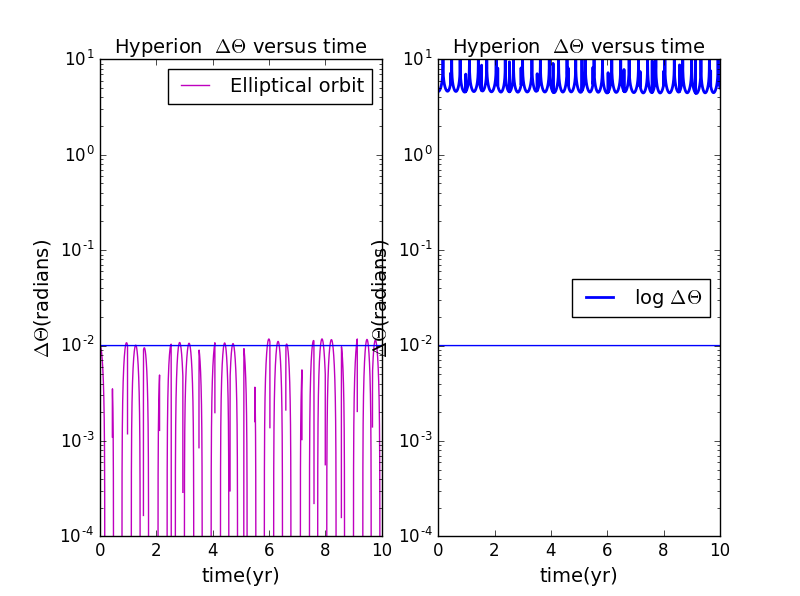
import matplotlib.pyplot as plt
import numpy as np
from pylab import *
import math
class hyperion:
def init(self,GM=4*math.pi**2,dt=0.0001,time=10):
self.GM=GM
self.e=e
self.x1=[1.05]
self.y1=[0]
self.vx1=[0]
self.vy1=6
self.x2=[1.05]
self.y2=[0]
self.vx2=[0]
self.vy2=6
self.dt=dt
self.time=time
self.r1=[math.sqrt(self.x1[0]**2+self.y1[0]**2)]
self.r2=[math.sqrt(self.x2[0]**2+self.y2[0]**2)]
self.t=[0]
self.w1=[0]
self.theta1=[0]
self.w2=[0]
self.theta2=[0.01]
self.Deltatheta=[0.01]
self.L=[0]
def calculate(self):
for i in range(int(self.time//self.dt)):
self.vx1.append(self.vx1[i]-self.GM*self.x1[i]*self.dt/self.r1[i]**3)
self.vy1.append(self.vy1[i]-self.GM*self.y1[i]*self.dt/self.r1[i]**3)
self.x1.append(self.x1[i]+self.vx1[i+1]*self.dt)
self.y1.append(self.y1[i]+self.vy1[i+1]*self.dt)
self.r1.append(math.sqrt(self.x1[i+1]**2+self.y1[i+1]**2))
self.w1.append(self.w1[i]-3*self.GM/self.r1[i]**5*(self.x1[i]*math.sin(self.theta1[i])-self.y1[i]math.cos(self.theta1[i]))(self.x1[i]*math.cos(self.theta1[i])+self.y1[i]*math.sin(self.theta1[i]))*self.dt)
self.theta1.append(self.theta1[i]+self.w1[i+1]*self.dt)
self.vx2.append(self.vx2[i]-self.GM*self.x2[i]*self.dt/self.r2[i]**3)
self.vy2.append(self.vy2[i]-self.GM*self.y2[i]*self.dt/self.r2[i]**3)
self.x2.append(self.x2[i]+self.vx2[i+1]*self.dt)
self.y2.append(self.y2[i]+self.vy2[i+1]*self.dt)
self.r2.append(math.sqrt(self.x2[i+1]**2+self.y2[i+1]**2))
self.w2.append(self.w2[i]-3*self.GM/self.r2[i]**5*(self.x2[i]*math.sin(self.theta2[i])-self.y2[i]math.cos(self.theta2[i]))(self.x2[i]*math.cos(self.theta2[i])+self.y2[i]*math.sin(self.theta2[i]))*self.dt)
self.theta2.append(self.theta2[i]+self.w2[i+1]*self.dt)
self.Deltatheta.append(abs(self.theta2[i])-abs(self.theta1[i]))
self.L.append(abs(math.log(abs(self.Deltatheta[i]))))
self.t.append(self.t[i]+self.dt)
if self.theta1[i+1]<-math.pi:
self.theta1[i+1]=self.theta1[i+1]+2*math.pi
if self.theta1[i+1]>math.pi:
self.theta1[i+1]=self.theta1[i+1]-2*math.pi
if self.theta2[i+1]<-math.pi:
self.theta2[i+1]=self.theta2[i+1]+2*math.pi
if self.theta2[i+1]>math.pi:
self.theta2[i+1]=self.theta2[i+1]-2*math.pi
def show_results(self,color):
subplot(121)
plt.plot(self.t,self.Deltatheta,'m',label=r'Elliptical orbit')
plt.title(r'Hyperion $\Delta$$\Theta$ versus time',fontsize=14)
plt.xlabel(u'time(yr)',fontsize=14)
plt.ylabel(u'$\Delta$$\Theta$(radians)',fontsize=14)
plt.xticks([0,2,4,6,8,10])
plt.xlim(0,10)
plt.ylim(0.0001,10)
plt.legend(fontsize=14,loc='best')
plt.semilogy(self.Deltatheta)
subplot(122)
plt.plot(self.t,self.L,color="blue",label="log $\Delta$$\Theta$",linewidth=2)
plt.title(r'Hyperion $\Delta$$\Theta$ versus time',fontsize=14)
plt.xlabel(u'time(yr)',fontsize=14)
plt.ylabel(u'$\Delta$$\Theta$(radians)',fontsize=14)
plt.xticks([0,2,4,6,8,10])
plt.xlim(0,10)
plt.ylim(0.0001,10)
plt.legend(fontsize=14,loc='best')
plt.semilogy(self.Deltatheta)
a=hyperion()
a.calculate()
a.show_results('b')
plt.show()

(1)The behavior of Hyperion when $\theta$ is not restricted to the range of $-\pi$ to $\pi$ for $v_1={\frac{4{\pi}^2(1-e)}{a(1+e)}}^{1/2}=1$,when a=1 and e=0.95;

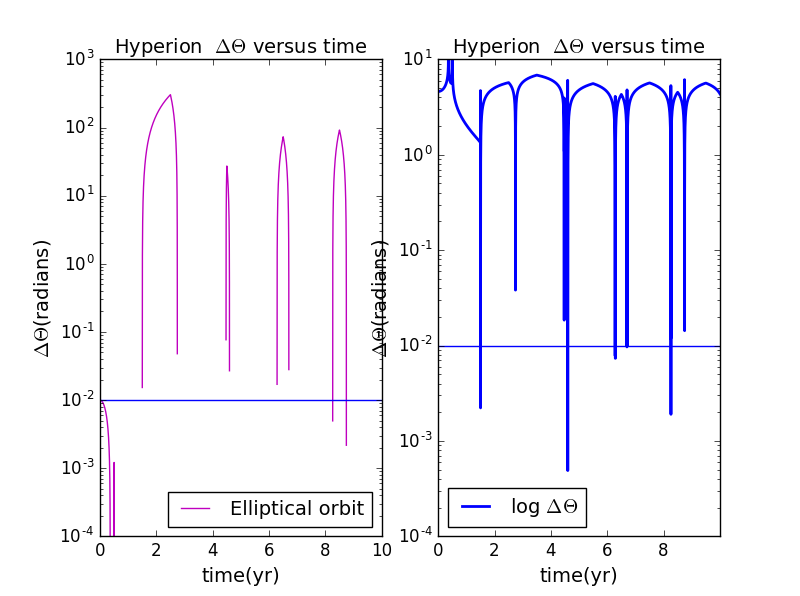
(2).when $v_1=3$ and e=0.629:

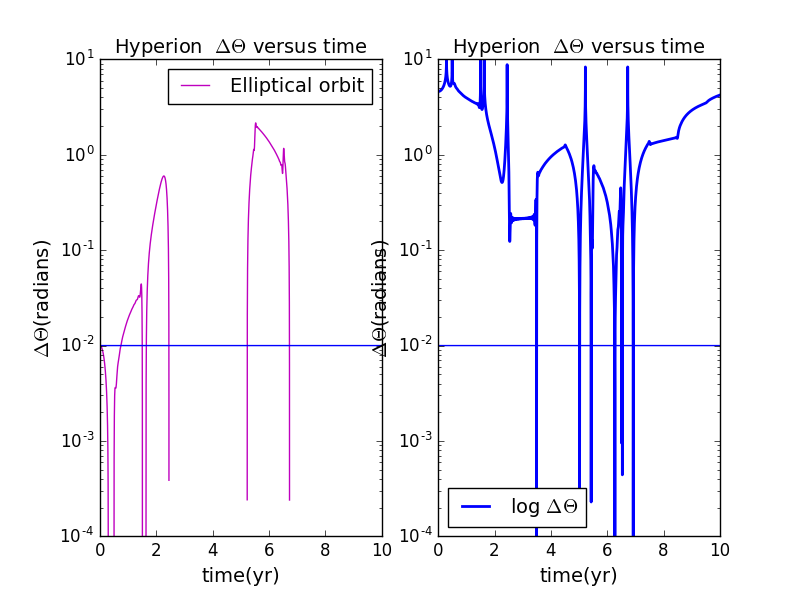
(3).when $v_1=4$ and e=0.423:

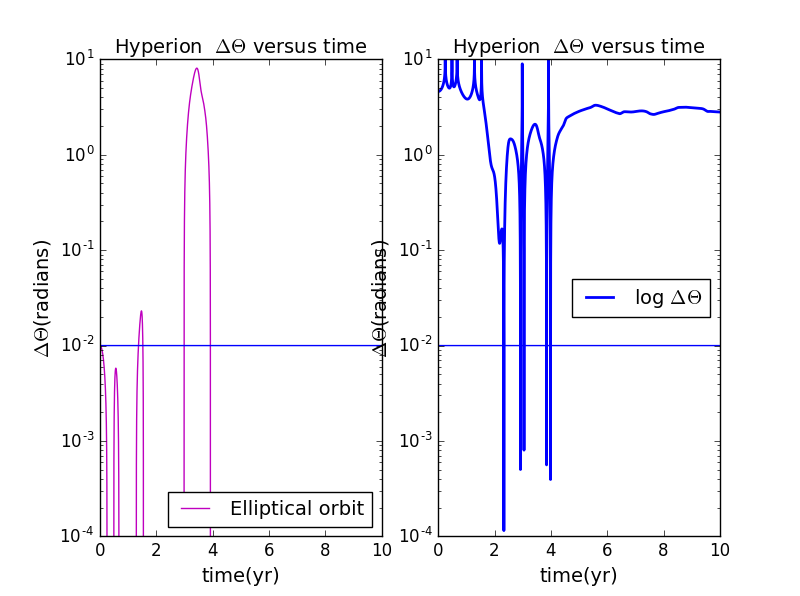
(4).when $v_1=5$ and e=0.225:

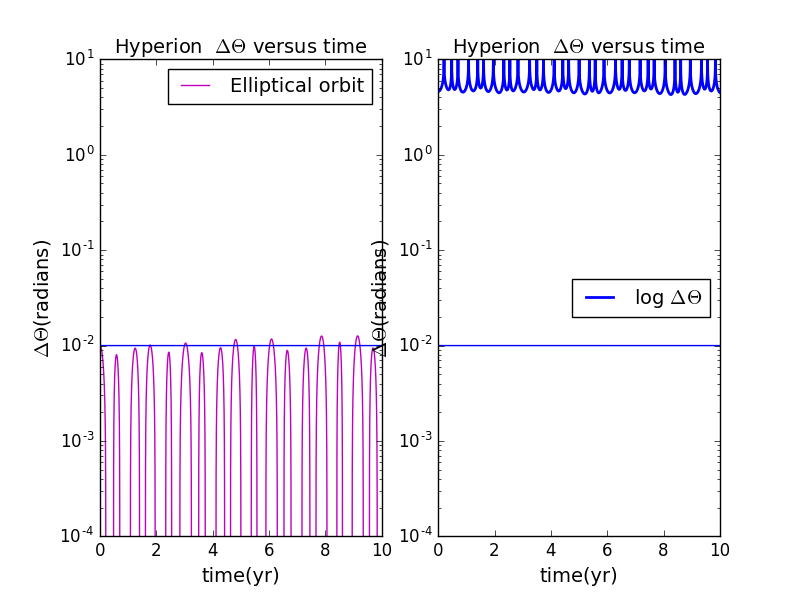
6.when $v_1=6$ and e=0.05:

if self.theta1[i+1]<-math.pi:
self.theta1[i+1]=self.theta1[i+1]+2*math.pi
if self.theta1[i+1]>math.pi:
self.theta1[i+1]=self.theta1[i+1]-2*math.pi
if self.theta2[i+1]<-math.pi:
self.theta2[i+1]=self.theta2[i+1]+2*math.pi
if self.theta2[i+1]>math.pi:
self.theta2[i+1]=self.theta2[i+1]-2*math.pi

四.结论:

五.致谢:

Thanks to 2014301510065 for reference.