Exercise_12:Chapter 5 Problem 5.4&5.7:Electric potentials andfields of two capacitor

一摘要：

Investigate how the magnitude of the fringing field of a parallel plate capacitor varies as a function of the plate seperation;And using the Gauss-Seidel method to solve the capacitor problem of Figures 5.6&5.7.

二背景介绍：

（1）①.Laplace's equation: $$\frac{\partial^2 V}{\partial x^2}+\frac{\partial^2 V}{\partial y^2}+\frac{\partial^2 V}{\partial z^2}=0,(5.1)$$

②. $$\frac{\partial V}{\partial x}=\frac{V(i+1,j,k)-V(i-1,j,k)}{2*\Delta{x}},(5.2)$$ $$\frac{\partial^2 V}{\partial x^2}=\frac{V(i+1,j,k)+V(i-1,j,k)-2V(i,j,k)}{(\Delta{x}^2},(5.3)$$ $$V(i,j,k)=\frac{1}{6}*[V(i+1,j,k)+V(i-1,j,k)+V(i,j+1,k)+V(i,j-1,k)+V(i,j,k+1)+V(i,j,k-1)],(5.4)$$

(2)A two-dimensional problem of calculating the electric potential inside the square box: $$V(i,j)=\frac{1}{4}*[V(i+1,j,k)+V(i-1,j,k)+V(i,j+1,k)+V(i,j-1,k)],(5.5)$$ $$E_x=-\frac{\partial V}{\partial x},(5.6)$$ $$E_x(i,j)=-\frac{V(i+1,j)-V(i-1,j)}{2*\Delta{x}},(5.7)$$

(3)The Jacobi method: $$V_{new}(i,j)=\frac{1}{4}*[V_{old}(i+1,j)+V_{old}(i-1,j)+V_{old}(i,j+1)+V_{old}(i,j-1)],(5.8)$$

(4)The Gauss-Seidel method: $$V_{new}(i,j)=\frac{1}{4}*[V_{old}(i+1,j)+V_{new}(i-1,j)+V_{old}(i,j+1)+V_{new}(i,j-1)],(5.9)$$

三正文：

1.$\Delta{V}=10$:

(1)the plate separation is 0,and the number of iterations is 42:

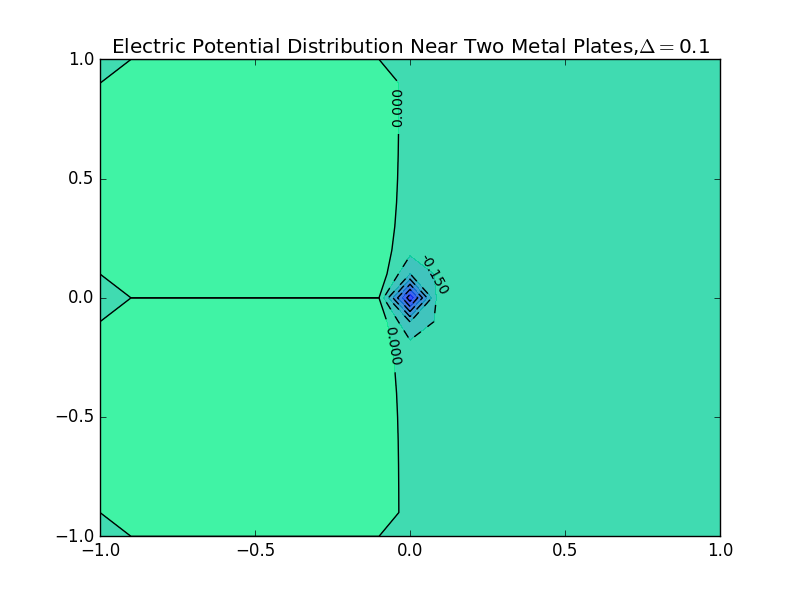
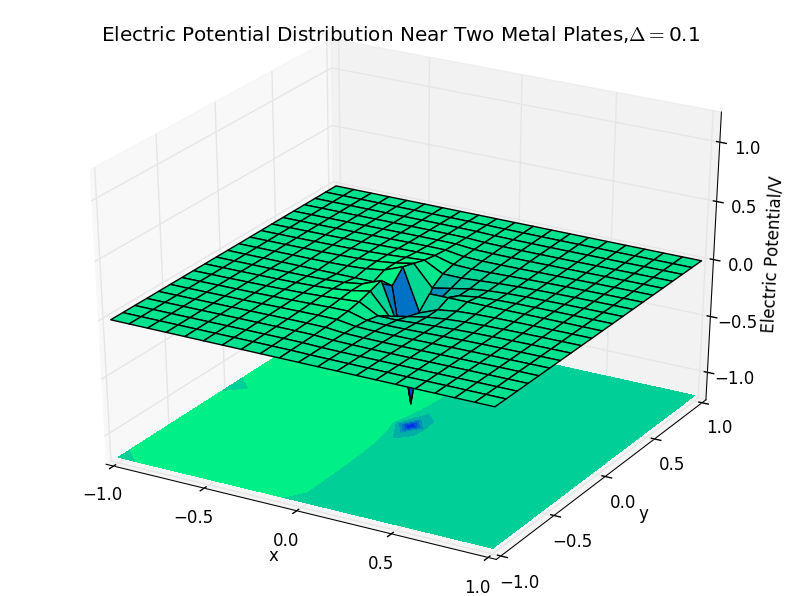
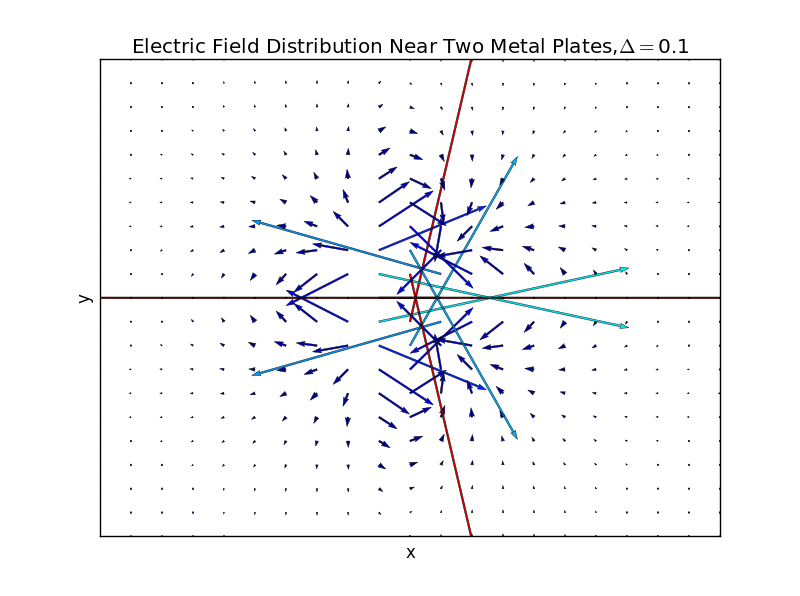
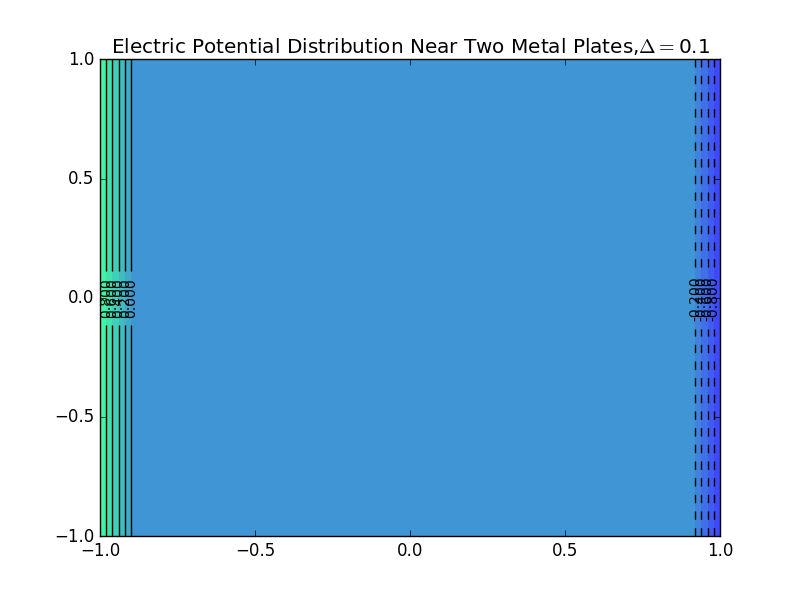
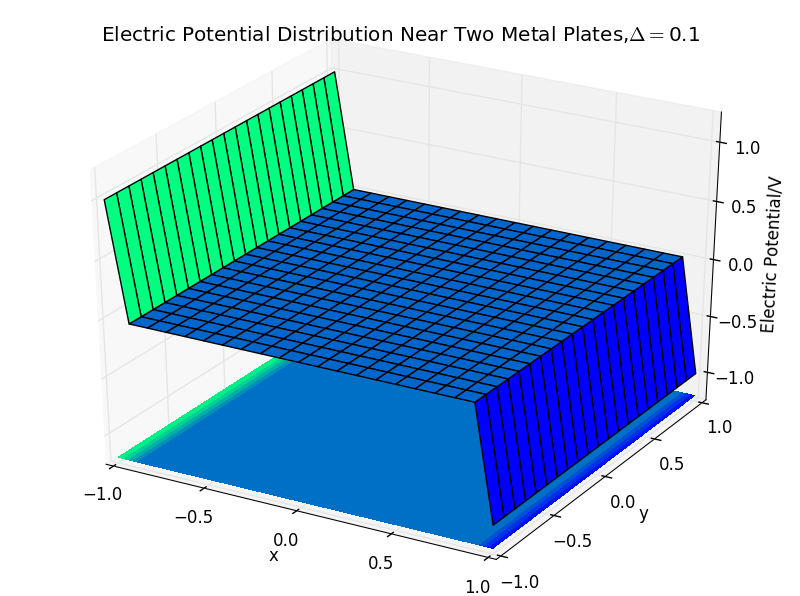
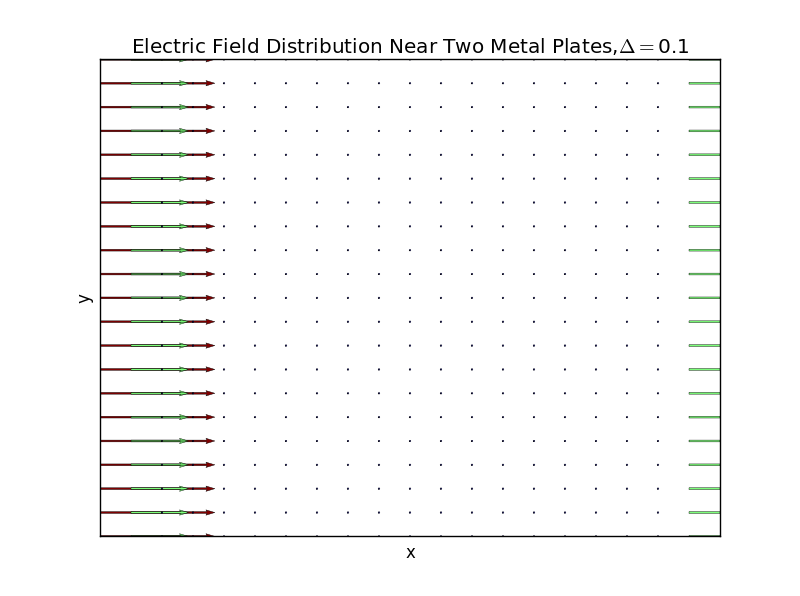
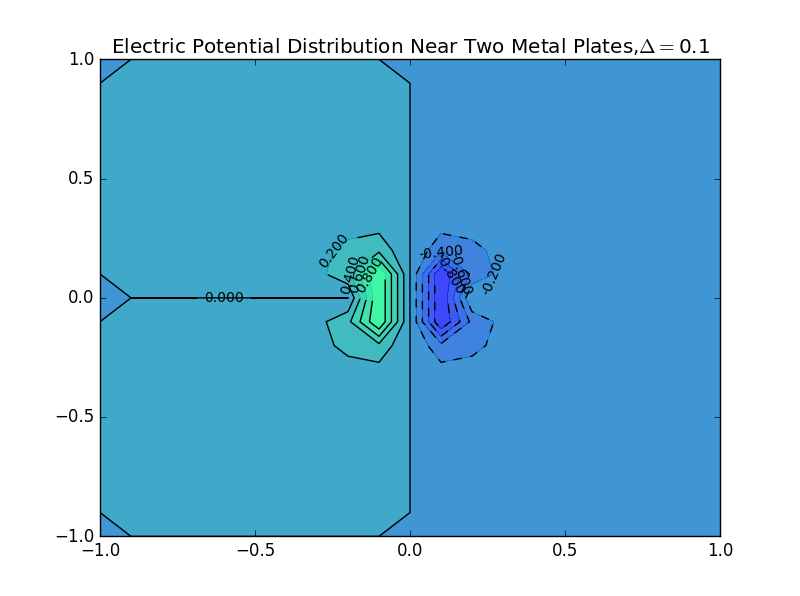
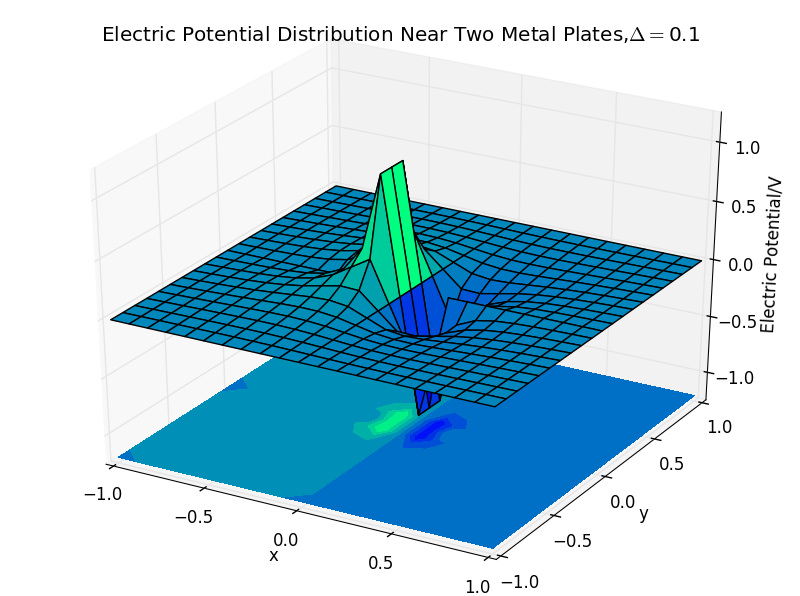
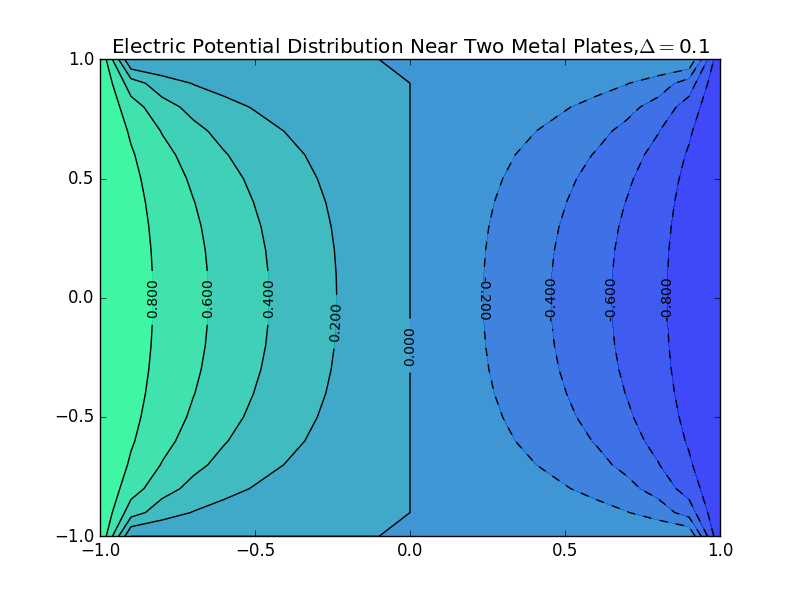
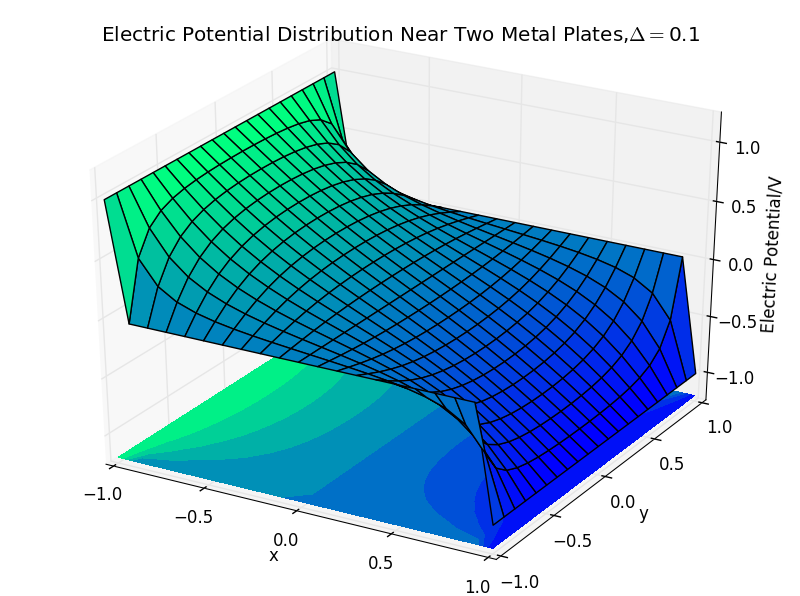
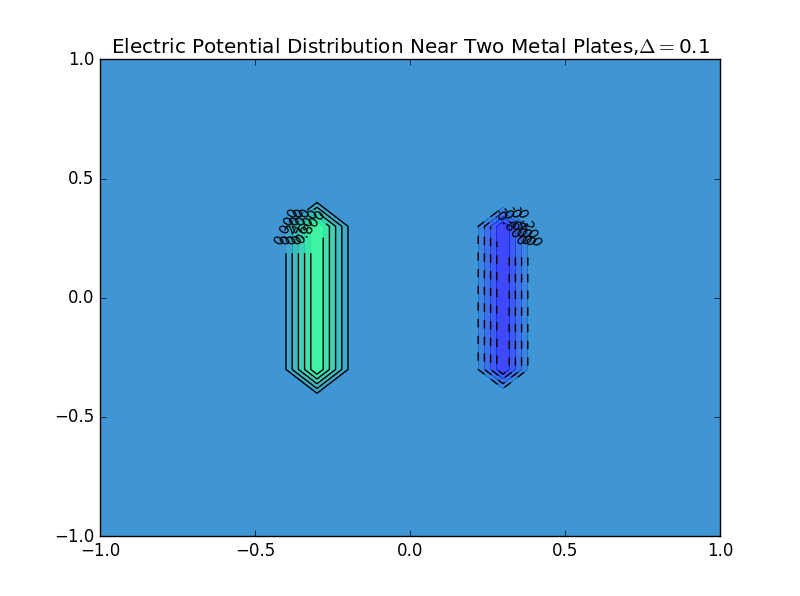
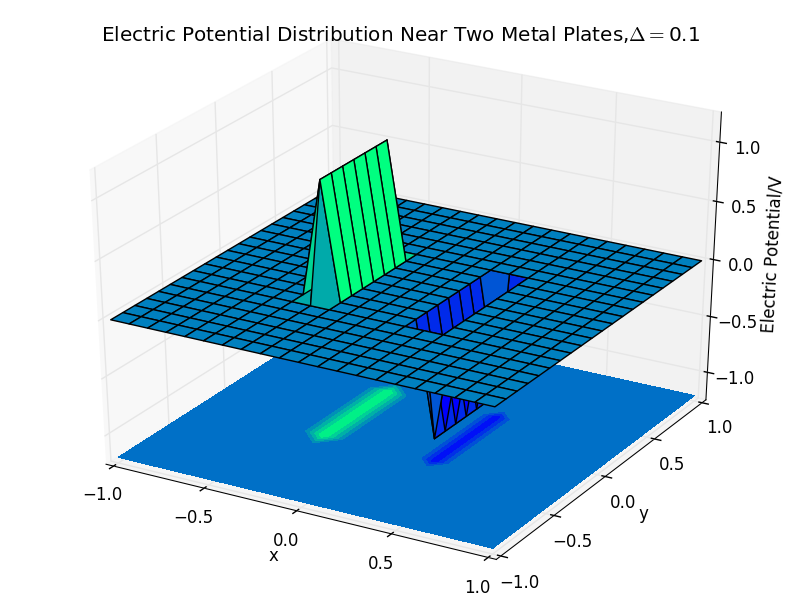
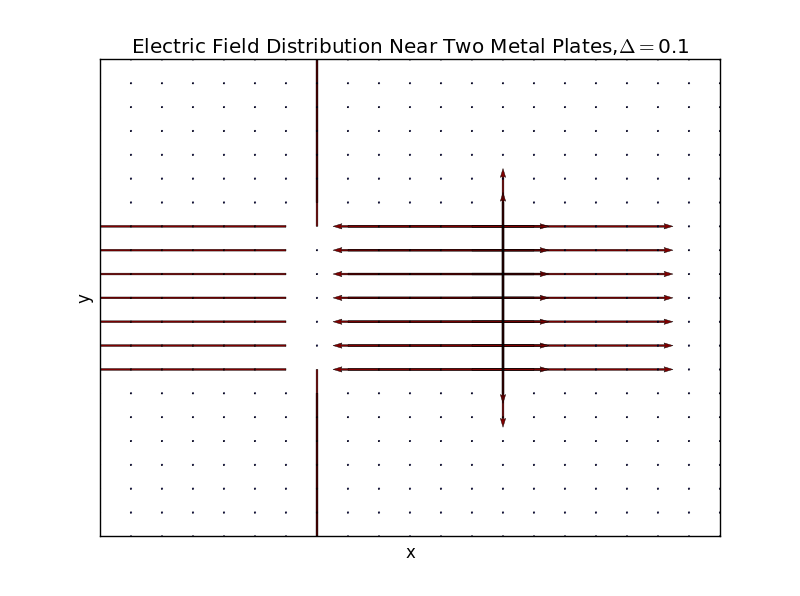
(2)the plate separation is 0.1,and the number of iterations is 50:



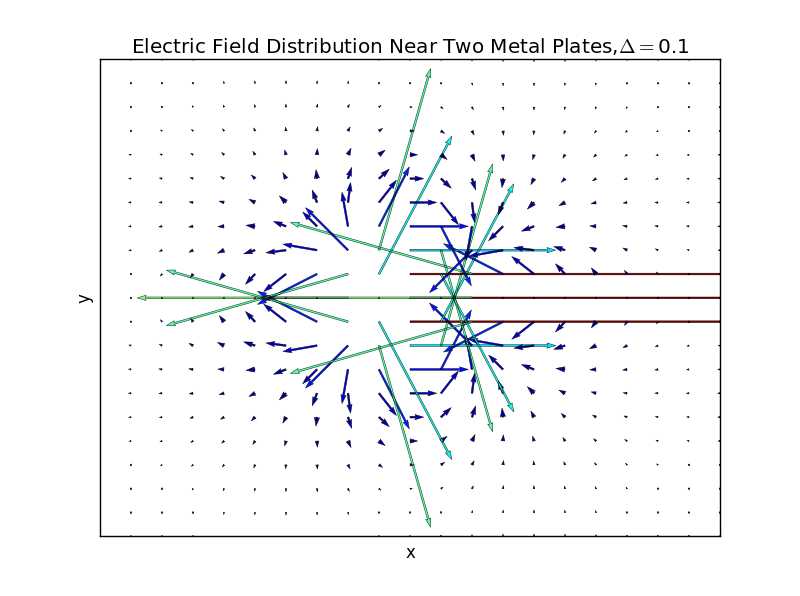
(3)the plate separation is 0.3,and the number of iterations is 57:



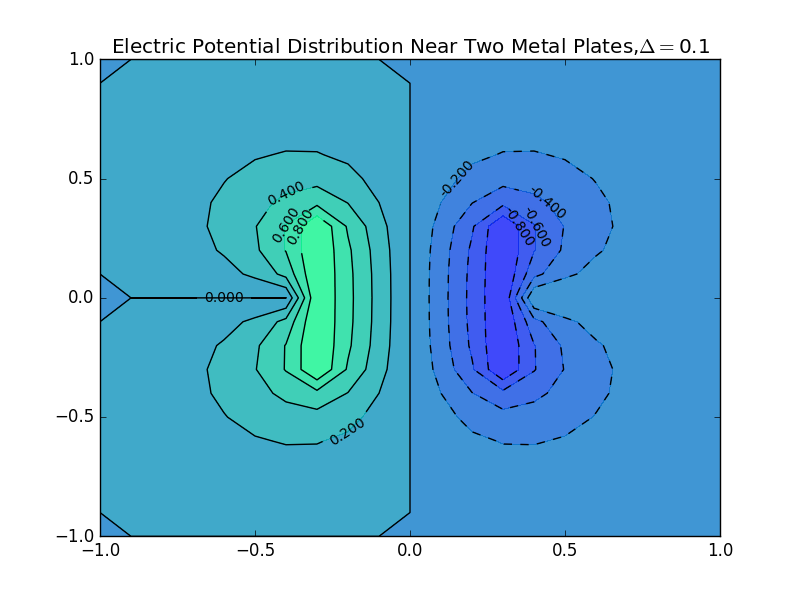
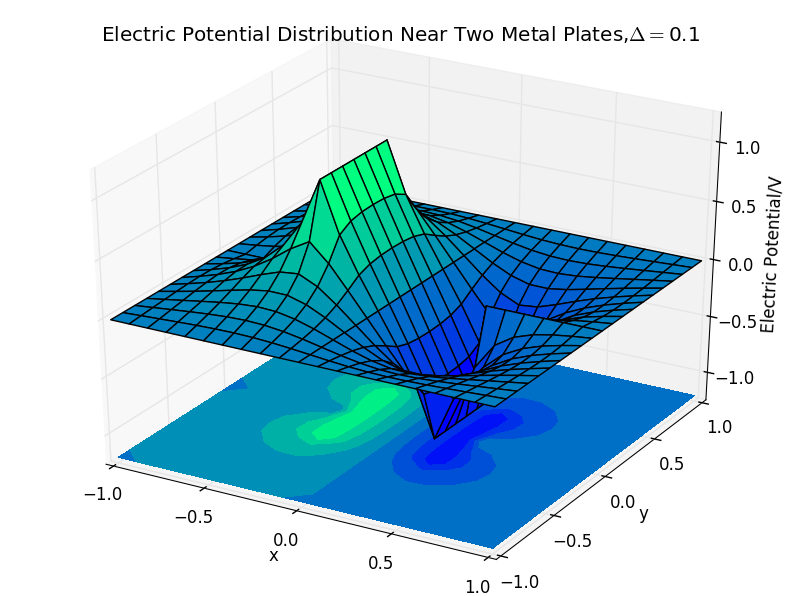
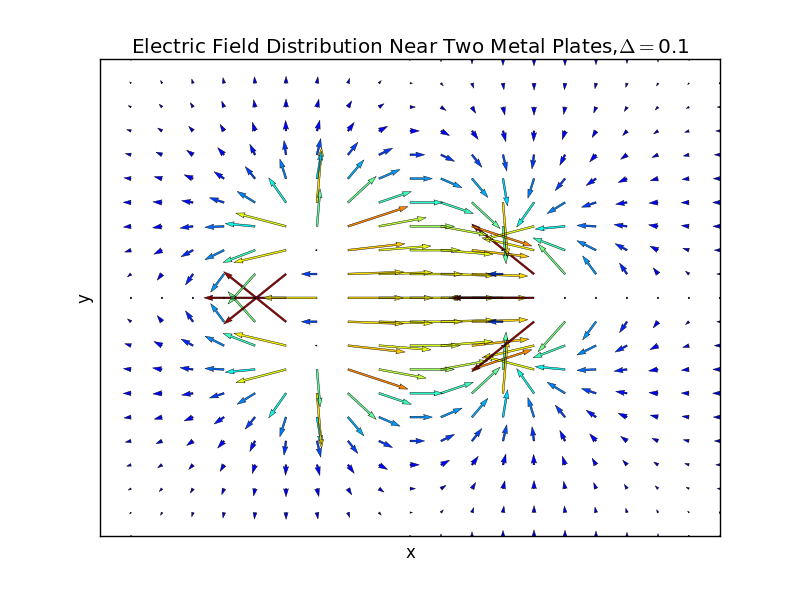
(4)the plate separation is 0.5,and the number of iterations is 46:



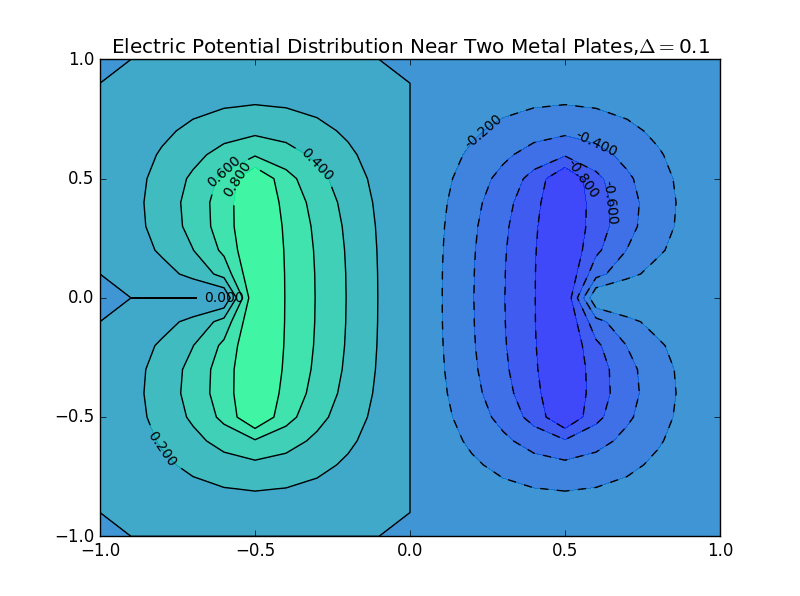
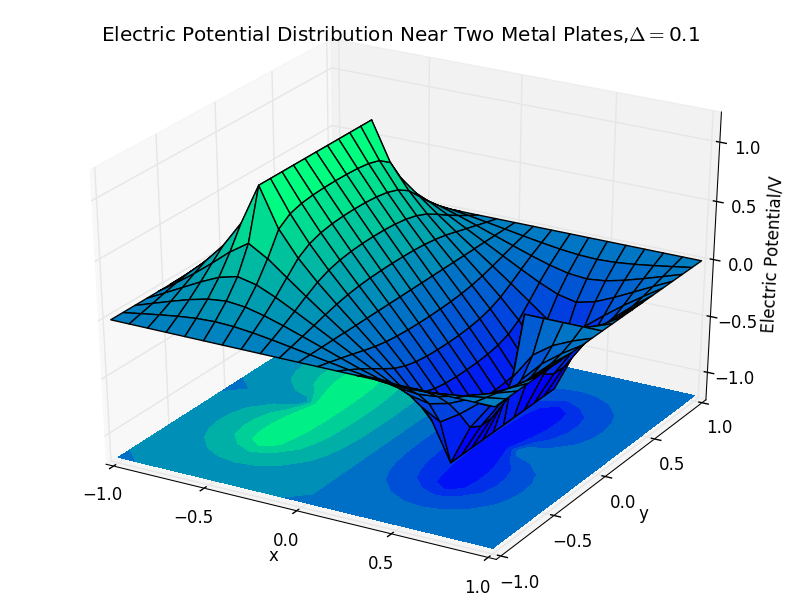
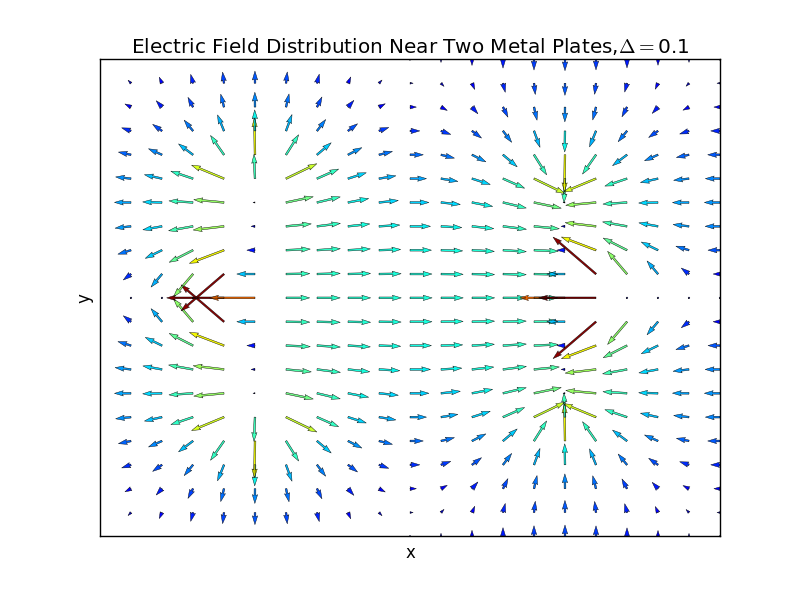
(5)the plate separation is 0.9,and the number of iterations is 103:



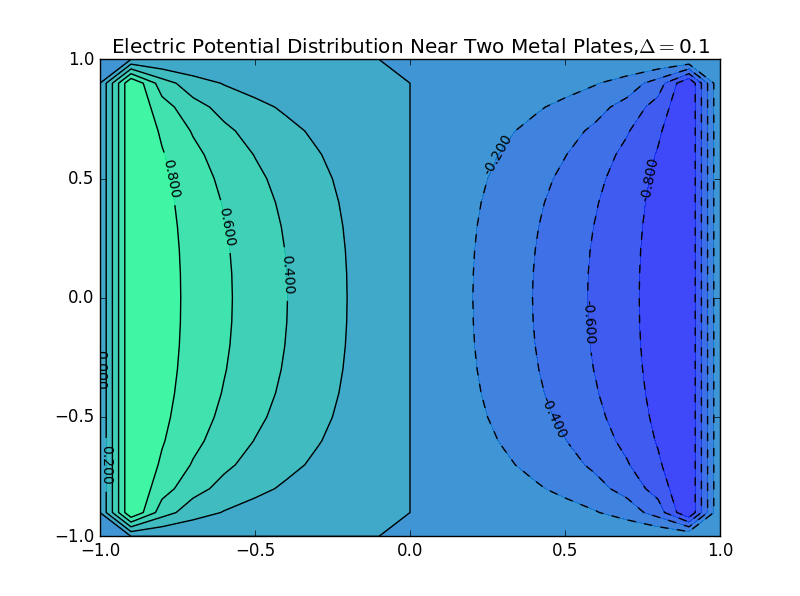
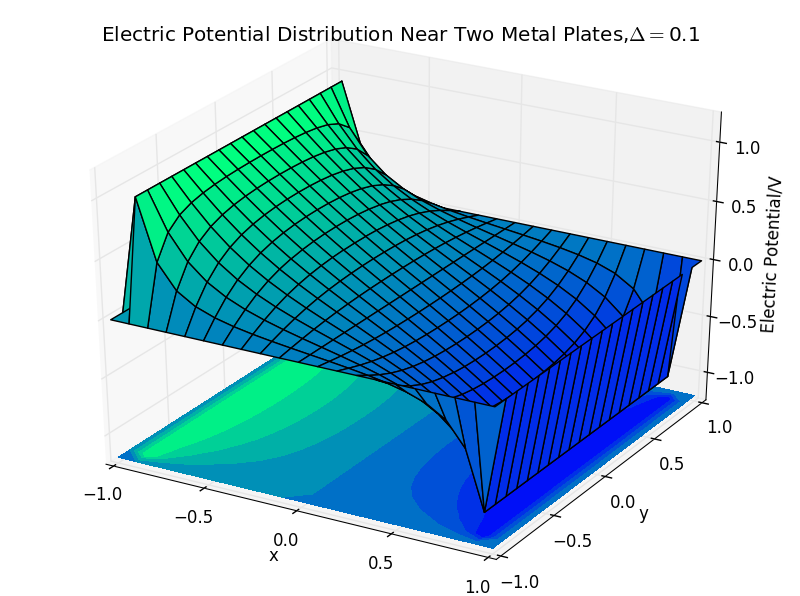
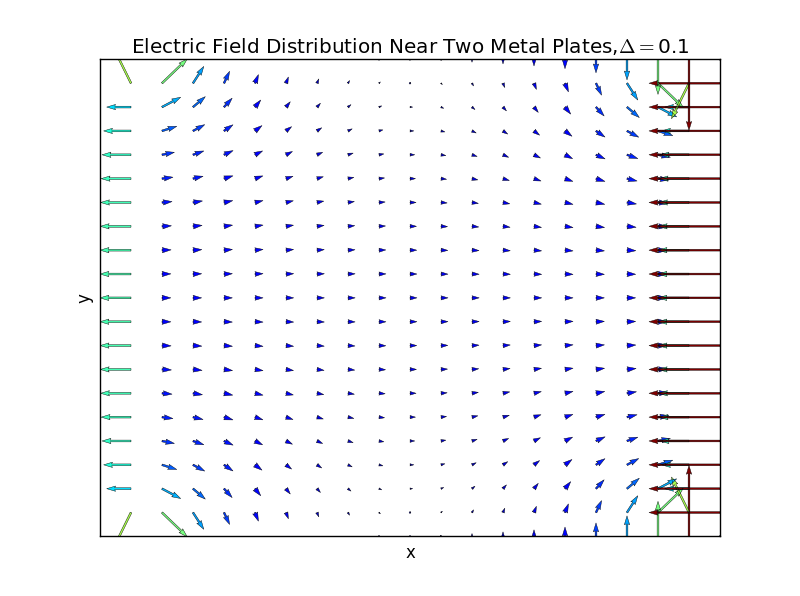
(6)the plate separation is 1.0,and the number of iterations is 120:

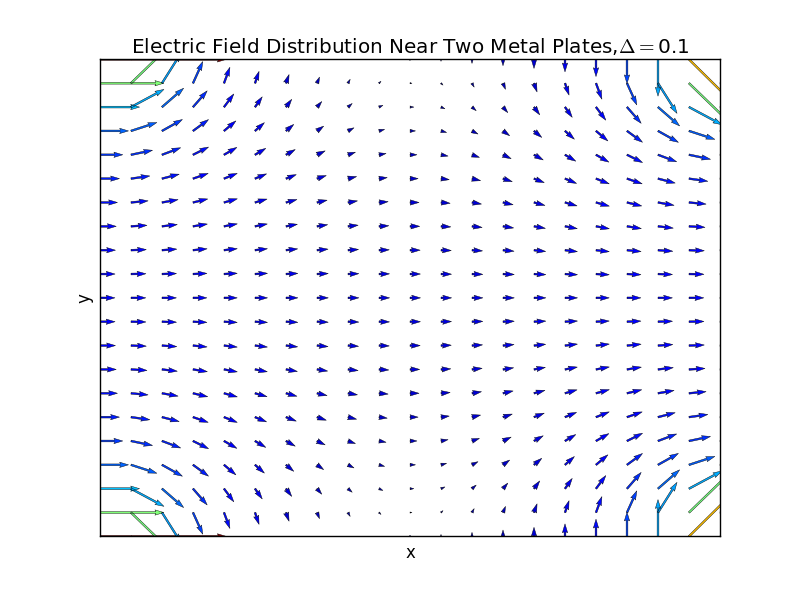
2.$\Delta{V}=0$:

(1).the plate separation is 0,and the number of iterations is 0:

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
delta=0.1
deltaV,times=0,0
1.initialize-V
V=[[0.]*(int(1+1/delta))for i in range(int(1+1/delta))]
for i in range(1+int(round(0.3/delta))):#boundary conditions tips: int(0.3/0.1)=2 why?????
V[int(round(0.3/delta))][i]=-1.
#2.calculation
def GS(V_old):#function to update-V
m=int(round(0.3/delta))
V_new=[[0.]*len(V_old)for i in range(len(V_old))]
for l in range(1+m):
V_new[m][l]=-1.
for j in range(1,len(V_old)-1):#boundary of x=0 or i=0 while 0 V_new[0][j]=(V_new[0][j-1]+V_old[0][j+1])/4
for i in range(1,m):
V_new[i][0]=(V_new[i-1][0]+V_old[i+1][0]+2*V_oldi)/4
for j in range(1,len(V_old)-1):
V_new[i][j]=(V_new[i-1][j]+V_old[i+1][j]+V_new[i][j-1]+V_old[i][j+1])/4
for j in range(m+1,len(V_old)-1):
V_new[m][j]=(V_new[m-1][j]+V_old[m+1][j]+V_new[m][j-1]+V_old[m][j+1])/4
for i in range(m+1,len(V_old)-1):
for j in range(1,len(V_old)-1):
V_new[i][j]=(V_new[i-1][j]+V_old[i+1][j]+V_new[i][j-1]+V_old[i][j+1])/4
v=[]
for i in range(len(V_old)):
v.append(reduce(lambda x,y:x+y,(map(lambda a,b:abs(a-b),V_old[i],V_new[i]))))
delta_V=reduce(lambda x,y:x+y,v)
return V_new,delta_V
3.loop and check the limit of deltaV
while deltaV > len(V)2*10(-5):#alternatively,for n in range(1):
V,deltaV=GS(V)#update
times=times+1#V is in the 1st Quadrant
print times
4.extend the potential to the interest regime to get V_whole
N=len(V)
V1=np.transpose(V)#1st Quadrant
V3=[[0.]*(N-1) for i in range(N)]#3rd quadrant
for i in range(N):
for j in range(N-1):
V3[i][j]=-V1[N-1-i][N-1-j]
add the 4th qudrant to V3 using extend
for i in range(N):
V3[i].extend(V1[N-1-i])
add the 1st&2nd qudrant using +
V_whole=V3
for i in range(N-1):
V_whole=V_whole+[V3[N-2-i]]
del V1,V3
check:print len(V_whole)

2D contour
plt.contourf(X, Y, V_whole, 10, alpha=.75, cmap='winter')
C = plt.contour(X, Y, V_whole, 10, colors='black', linewidth=.5)
plt.clabel(C, inline=1, fontsize=10)
plt.title(r'Electric Potential Distribution Near Two Metal Plates,$\Delta=$%s'%delta)
plt.show()

3D figure
fig = plt.figure()
ax = Axes3D(fig)
x=np.linspace(-1,1,len(V_whole))
X,Y= np.meshgrid(x,x)
ax.plot_surface(X,Y,V_whole, rstride=1, cstride=1, cmap='winter')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('Electric Potential/V')
ax.set_title(r'Electric Potential Distribution Near Two Metal Plates,$\Delta=$%s'%delta)
ax.set_xlim(-1,1)
ax.set_ylim(-1,1)
ax.set_zlim(-1.2,1.2)
ax.contourf(X, Y, V_whole, zdir='z', offset=-1.2, cmap=plt.cm.winter)
plt.show()

2D electric field plot
EY,EX=np.gradient(V_whole)
EX,EY=-EX,-EY
R=np.sqrt(EX**2+EY**2)
plt.quiver(X,Y,EX,EY,R, alpha=5)
plt.quiver(X,Y,EX,EY, edgecolor='k', facecolor='None', linewidth=.3)
plt.title(r'Electric Field Distribution Near Two Metal Plates,$\Delta=$%s'%delta)
plt.xlabel('x'),plt.ylabel('y'),
plt.xlim(-1.,1.), plt.xticks([])
plt.ylim(-1.,1.), plt.yticks([])
plt.show()

(2).the plate separation is 0.3,and the number of iterations is 0:



(3).the plate separation is 1.0,and the number of iterations is 0:

四结论：

1.When $\Delta{V}=0$,no matter how much the plate separation is,the number of iterations is 0;While that of $\Delta{V}$ is nonzero is not;

2.When the plate separation is 1,the electric field is uniform electric field no matter how much $\Delta{V}$ is;

3.When the plate separation is 0,the electric potential is similiar to a point charge.

五致谢：

Thanks to JunyiShangguan senior for making use of the program.