期末作业

4.7.Consider a hypothetical solar system consisting of a sun and one planet in which the mass of the sun is not much greater than the mass of the planet. Now you must allow for the motion of both the planet and the sun. Extend your planetary motion program to include this effect. You will have to deal with a set of equations such as those in(4.7) for both objects. Investigate the possible types of orbital motion found in such a system. Begin with a double star system in while the two objects are of equal mass. Then explore the behavior when the masses are unequal. Hint: In order to obtain the simplest orbits, it is best to pick initial conditions such that the total linear momentum is zero. While this problem can be handled with a stationary sun together with the concept of a reduced mass, this calculation is a necessary prelude to the study of orbits of planets in binary star systems,which wwe will consider in a later exercise.

Abstract

Simulation of solar system in three-dimension version will be made. In addition, Two body system and binary star system will be explored and displayed in three-dimension form.

Introduction

If we want to explore fundamental physical principles such as Newton's laws, we would better find a system without friction force. The solar system is such a ideal laboratory. 
Studying of the motion of celestial bodys is really inspiraing! We will begin with a sun and one planet system than go to binary star systems.

Numerical Approach

Euler-Cromer method is a better choice than Euler method on this problem. Because the planetary motion is a oscillatory problem.
If we use Euler method, the energy of the planet will go with time, but Euler-Cromer method can exactly conserve energy over the course of each orbit. So we will take the latter one for our problem.
Consider a simple system which has a sun and a planet, the dynamic equation can be written as:
$\frac{dv_{x}}{dt}=-\frac{GM_{S}x}{r^{3}}$
$\frac{dx}{dt}=v_{x}$
$\frac{dv_{y}}{dt}=-\frac{GM_{S}y}{r^{3}}$
$\frac{dy}{dt}=v_{y}$
We will use astronomical units,AU and use year to measure time, and we have $GM_{S}=v^{2}r$, for simplity we take the period as 1 year, than $v=\frac{2\pi r}{yr}$ so $GM_{s}=4\pi r^{3}$. For earth,r=1(AU) 
If we consider two body problem, in which has no fixed body, there will be8 equations:$v_{x1},v_{x2},v_{y1},v_{y2},x_{1},x_{2},y_{1},y_{2}$, and right hand of the equation will be $(x_{1}-x_{2})(x_{2}-x_{1})$ and so on.

Data analysis

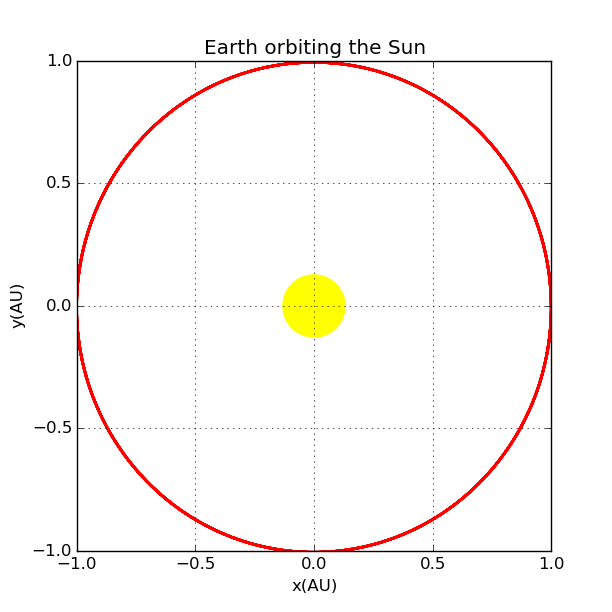
First, we start with the simplest situation: a system with Earth and Sun: 

Than we let the two bodys have equal mass: 
Notice that we should set the total momentum equals to zero, and the initial location is $(x_{1},y_{1})=(-1,0),(x_{2},y_{2})=(1,0)$; the initial velocity is $(v_{x1},v_{y1})=(0-\pi)(v_{x2},v_{y2})=(0,\pi )$:

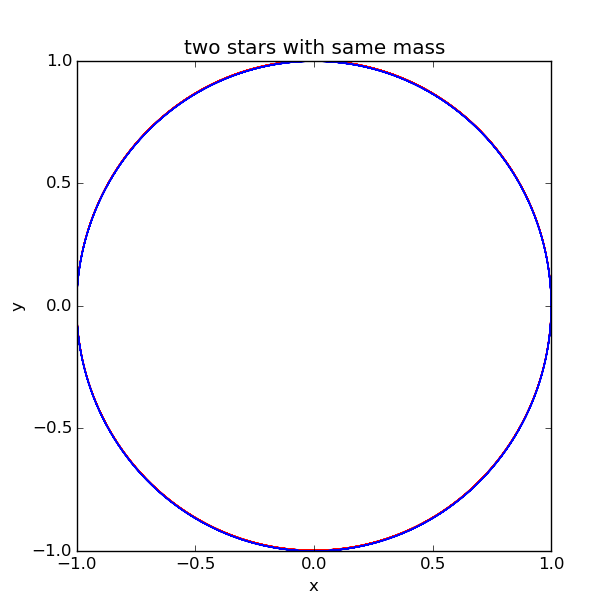
We can enlarge the figure to see it more clearly: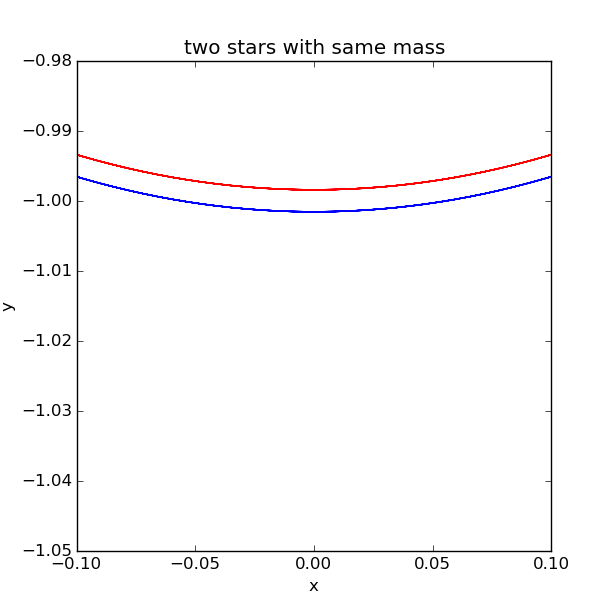
We can see the route is almost the same, but if we change the initial condition, the result will be totally differen. The result will change with initial conditions.

Conclusion

Today we construct our own solar system, and explore two body problem. When two body has same masses, their trajectory is symmetric, when they have different masses, the trajectory of the heavier one has a smaller radius. If one of it is extremely heavy, the radius get down to zero and it becomes a fixed body. Besides, the trajectory will vary with the initial condition.
期末程序.py未知大小