homework 7

习题3.12

解：物理摆的运动方程可以写为:
$\frac{d^{^{2}}\theta }{dt^{2}}=-\frac{g}{l}sin\theta -q\frac{d\theta }{dt}+F_{D}sin(\Omega _{D}t)$
关键是驱动力。当我们改变外力和驱动力时，混乱行为就会增加。
用欧拉克罗默法。
我们可以把运动方程重写为两个一阶方程:$\frac{dw }{dt}=-\frac{g}{l}sin\theta -q\frac{d\theta }{dt}+F_{D}sin(\Omega _{D}t)$
$\frac{d\vartheta }{dt}=w$
观察一个典型的物理钟摆在不同驱动力下的行为

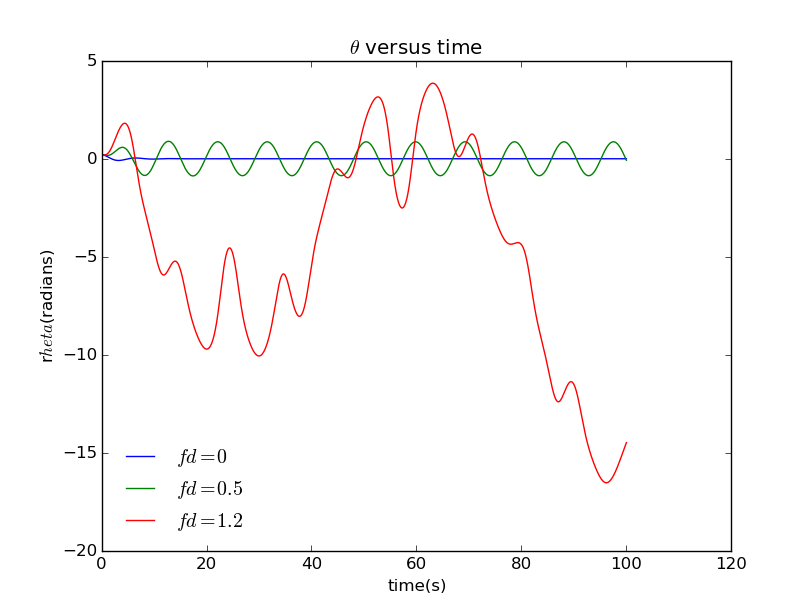
当$i\epsilon \left [ -\pi ,\pi \right ]$

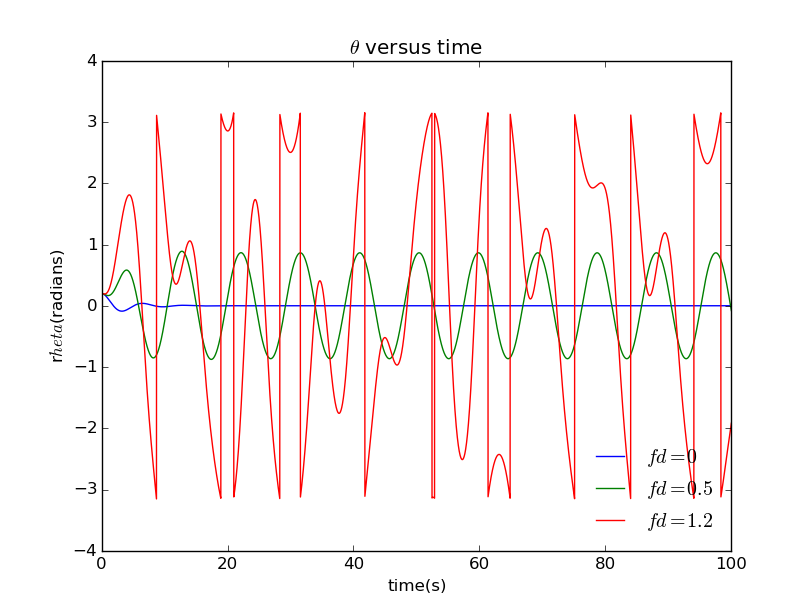
可以看到，物理摆的行为越来越随机，在低驱动下，运动是一个简单的振荡，它可以一直重复。但是，当高驱动时，钟摆的运动就变得复杂而不再重复。
两个相同的钟摆，我们以稍微不同的初始角度开始它们。
我们设定了初始的角度2.0000和2.0001，$F_{D}=0.5$

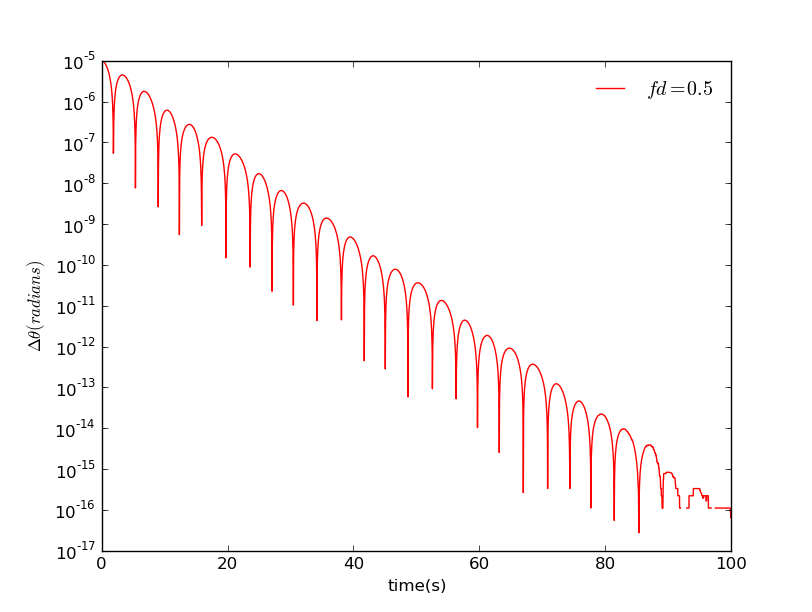
当我们把驱动力提高到1.2的时候

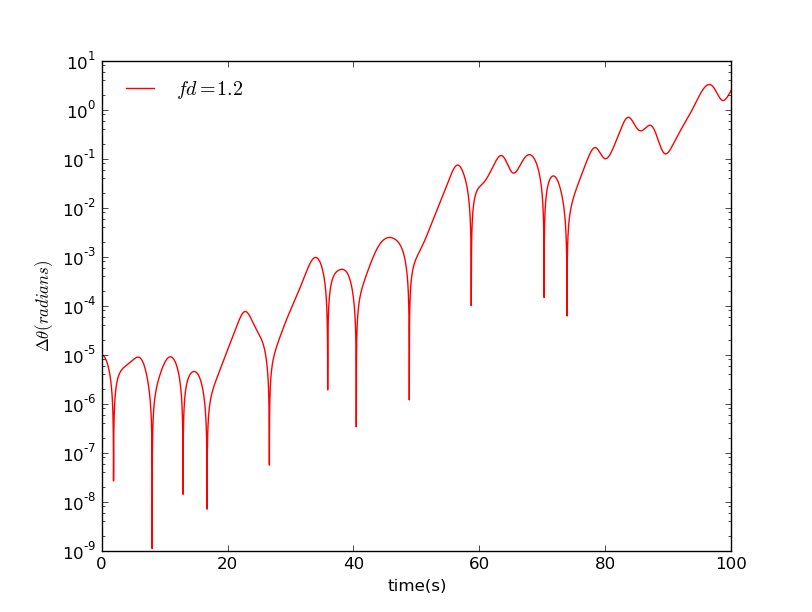
在第一个图中，驱动力是较小的，每3个都有一些非常陡的下降。当一个钟摆到达一个转折点时，就会出现这些下降。$\Delta \theta$将会在转折点附近消失，因为$\theta _{1}$和$\theta _{2}$轨迹必定交叉。总体而言，$\Delta \theta$呈现出平稳较快的下降趋势。这意味着两个钟摆的运动变得越来越相似。
与此相反，在第二个图中，有一个较大的驱动力，可以看到$\Delta \theta$随着时间快速增加且不规则，这一趋势意味着系统进入某种混乱状态。
为了描述这种现象，我们可以引入李亚普诺夫指数。有一个方程:
$\Delta \theta \approx e^{^{\lambda t}}$
当$\lambda =0$时，系统混乱
虽然物理摆是不可预测的，但有可能做出某些准确的预测。把这一波的速度画出来作为一个函数，它被称为相空间图。
有一个小的驱动力和一个较大的驱动力:

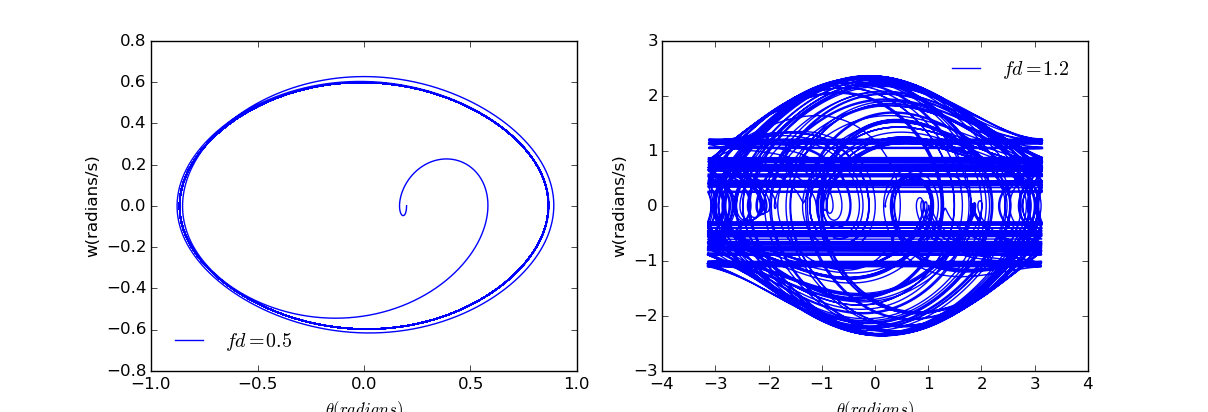
当驱动力很小的时候，图像很快就会进入一个正常的轨道。但是当力变大时，轨迹会呈现出许多接近闭合的轨道，且图案非常复杂，这是混沌系统的一个共同特征。
更重要的是，当$\Omega _{D}t=2n\pi$我们只能显示一个点,如果系统有一个固定的周期，相空间图只会显示一个点:

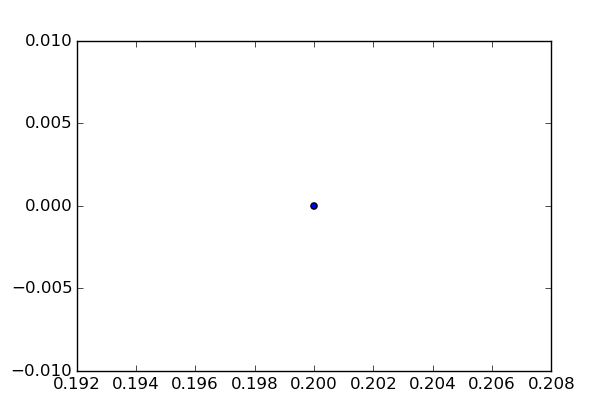
当提高驱动力时：

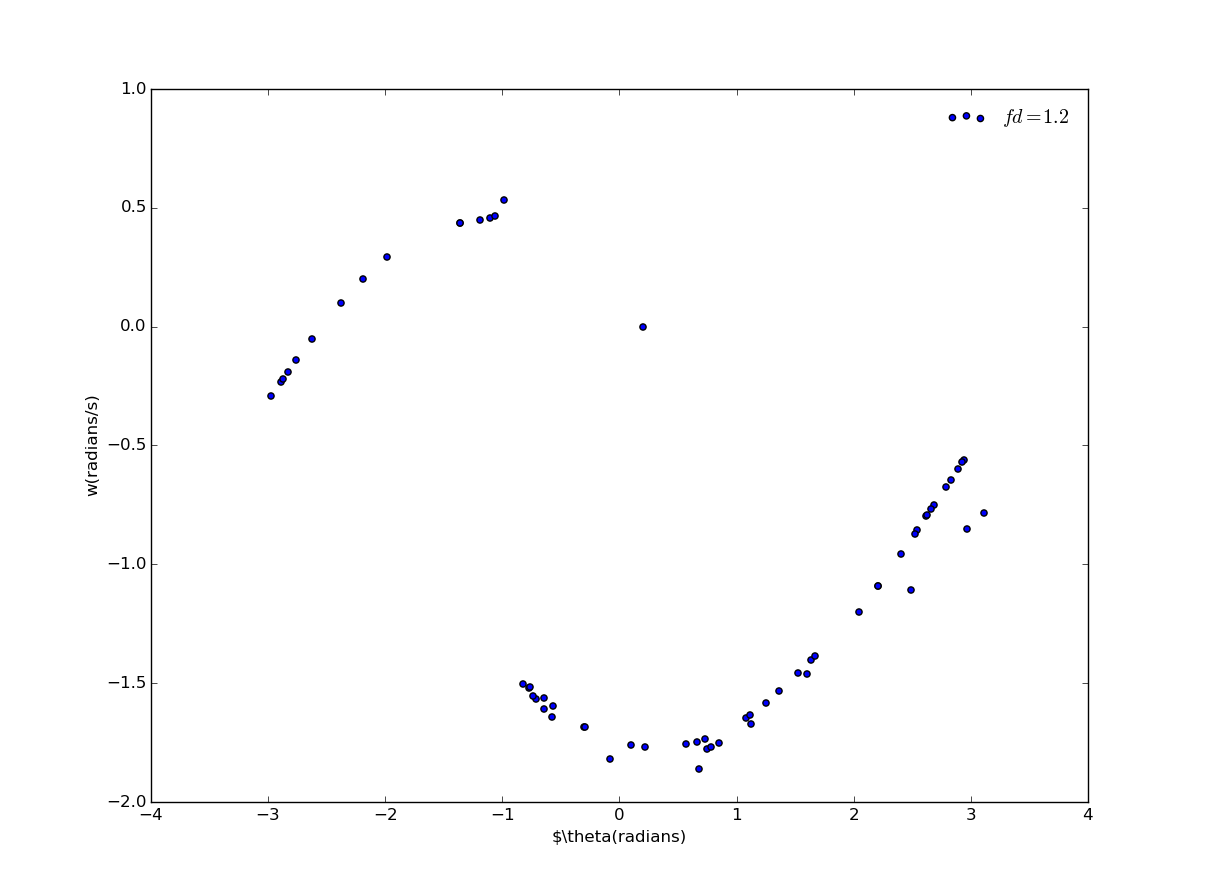
可以看到，当系统混乱时，轨迹是非常不同的。我们可以清楚地知道这个运动没有周期，这些点叫做吸引子。虽然吸引子在非混沌情况下具有简单的形式，但作为前一种，它们在混沌状态下具有非常复杂的结构，具有分形结构，称为奇异吸引子。
改变驱动力：


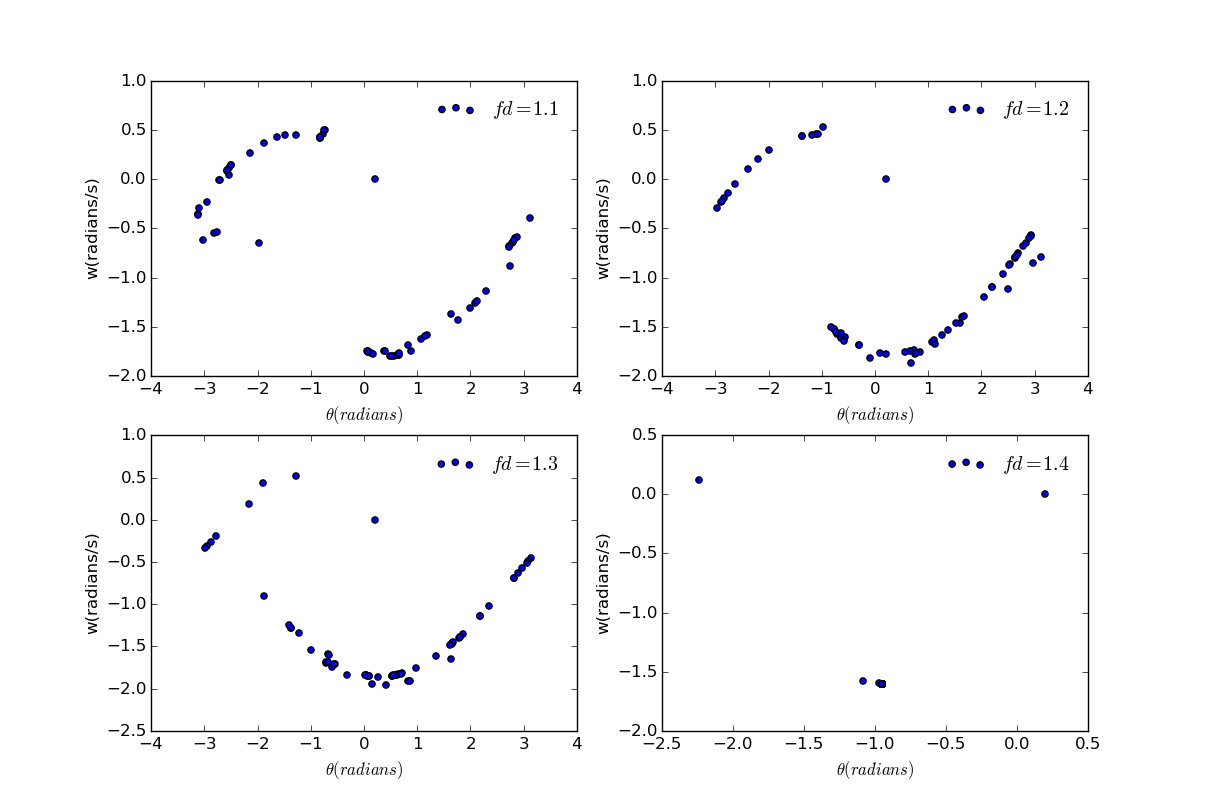
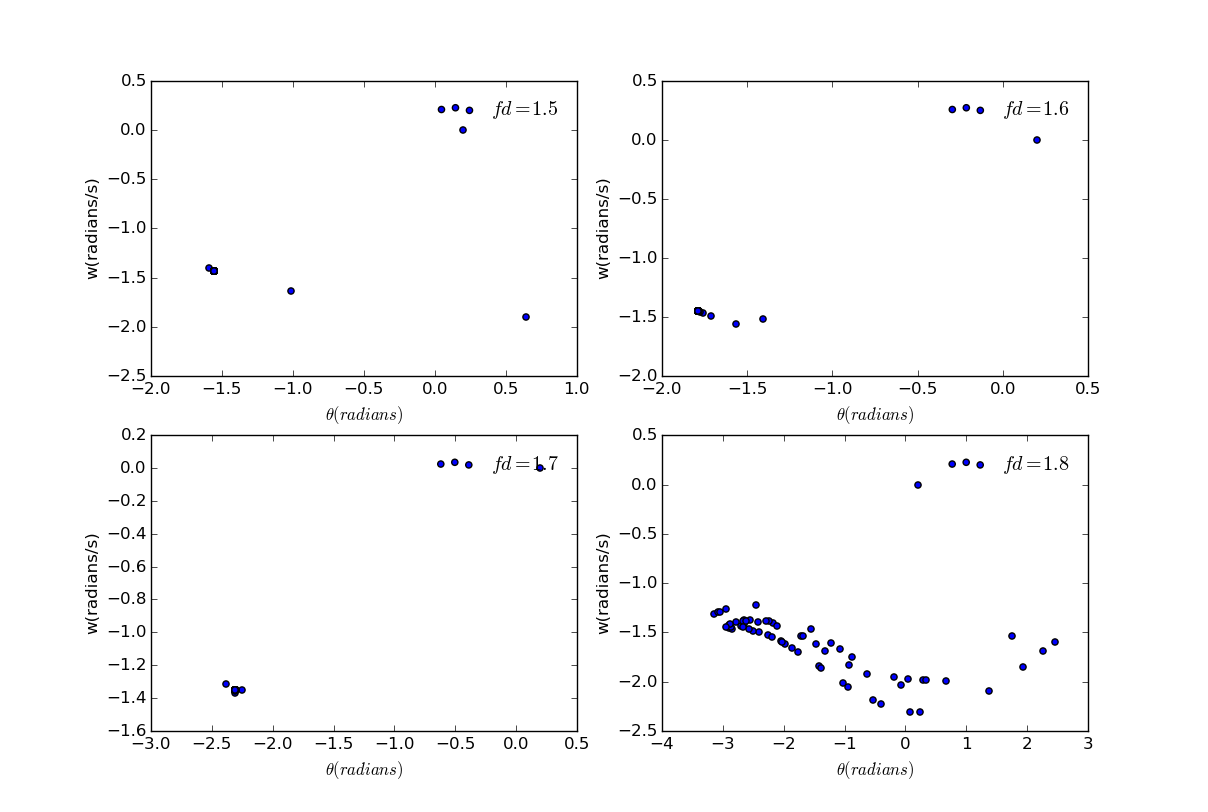
随着驱动力的增加，轨迹不会变得越来越随机，相反，它会变得有点规律，然后又变成随机的。总而言之，这个轨迹是不可预测的。
如果我们选择在不同的时间进行策划，会出现一些新的现象:
$\Omega _{D}=\frac{\pi }{2} ，\pi ，\frac{3\pi }{2}，2\pi$

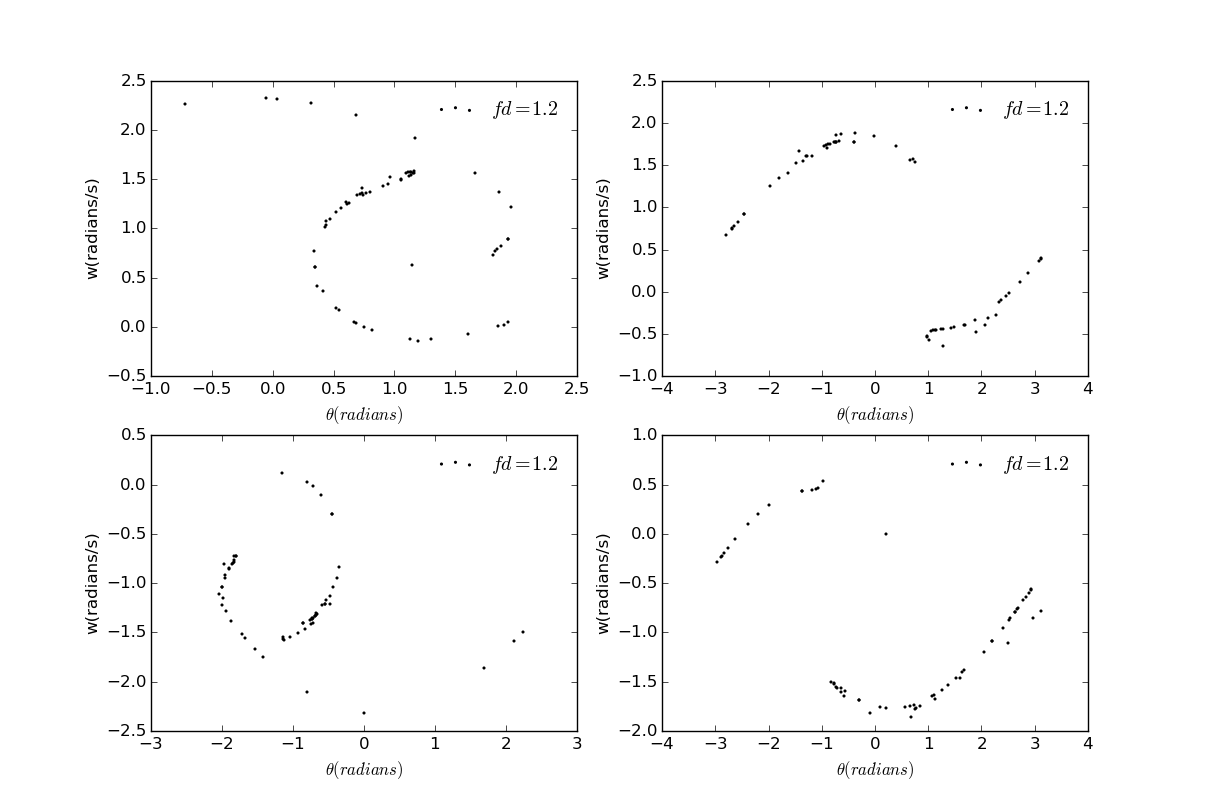
当$\Omega _{D}=\frac{\pi }{2} ，\frac{3\pi }{2}$时，驱动力达到最大值，当$\Omega _{D}=\pi ，2\pi$时，驱动力为零。
结论：
混沌系统有两个关键特性:它们都是决定性的和不可预测的;
混沌系统的行为不是完全随机的，可以用相空间中的奇异吸引子来描述。
程序