homework11(Two planet system)

作业

---

name:姚逸飞
student number：2013301020096

Homework

• $\Bbb homework\; L:$Two planet system

Abstract

This passage is mainly discuss about two planet system under the gravity force.Gravity is an very calssic force .It aws studied since 300 years ago.
The gravity of two planets is direct propotion to thier masses, and inverse popotion to their distance's square. So this passage will see what the trace of the two planets under the gravity force .And it will figure out what will happan if the gravity is not inverse the distance's square. It means that q is not zero .
Here I want to set an very interesting website. In this website, one can creat some different particals which has different mass and initial velocity, and then you can see how this particals move and can see the trace of them.
http://www.nowykurier.com/toys/gravity/gravity.html

Passage

Formost we give the gravity of the two planets as follows:

$$\vec{F} = G\frac{M_1M_2}{r^2}\hat{r}$$
In the caculation, we choose the $2M_1=M_2$. If the system is stable, we can know that the two planet driven by the same force
$$M_1\omega^2r_1=M_2\omega^2r_2$$
$$\frac{v_1}{v_2}=\sqrt{\frac{M_2r_2}{M_1r_1}}$$

Then we can give the two planets under the gavity.
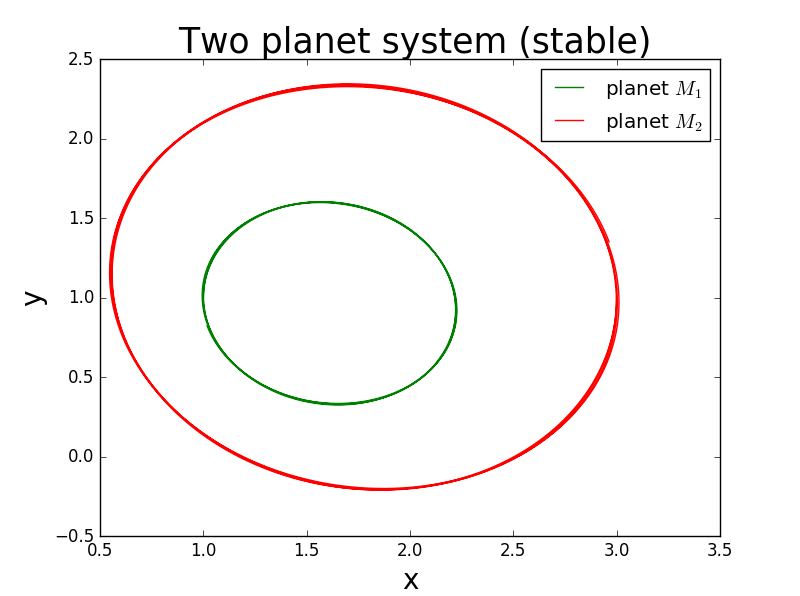
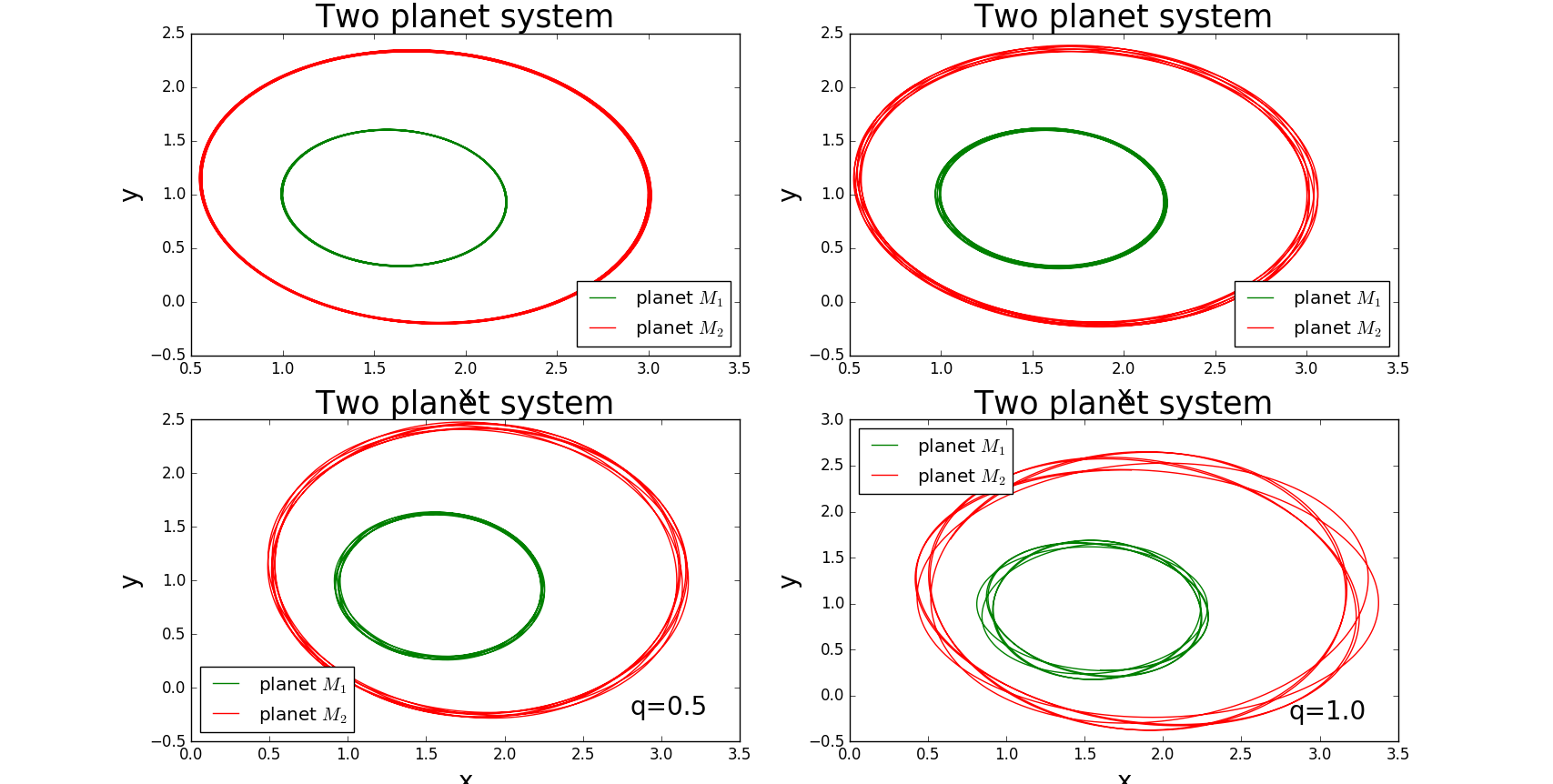
The first picture is when the two panets has the similar mass .Then they will be both stable.

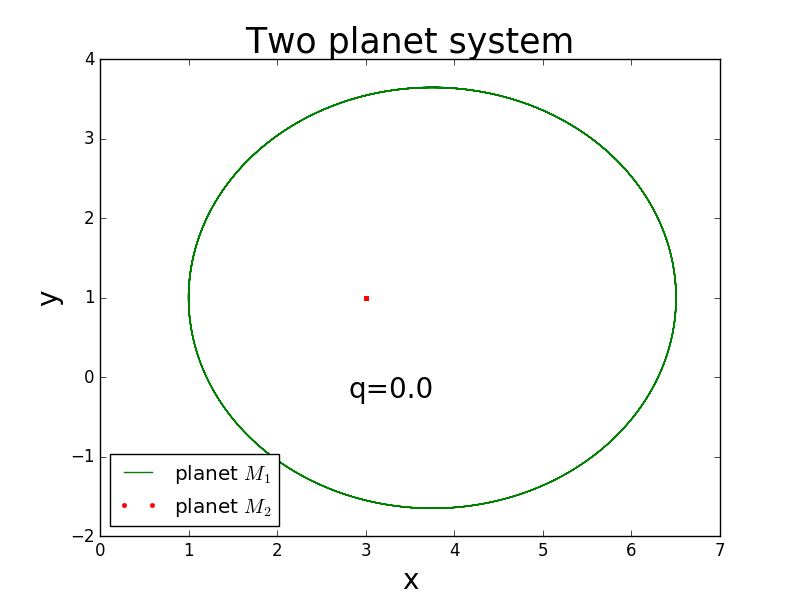
The second picture is when one planet has a huge mass ,then we can consider it is still. And then the other planet will round with it.

This picture is when the force is not inverse with the distance's square.

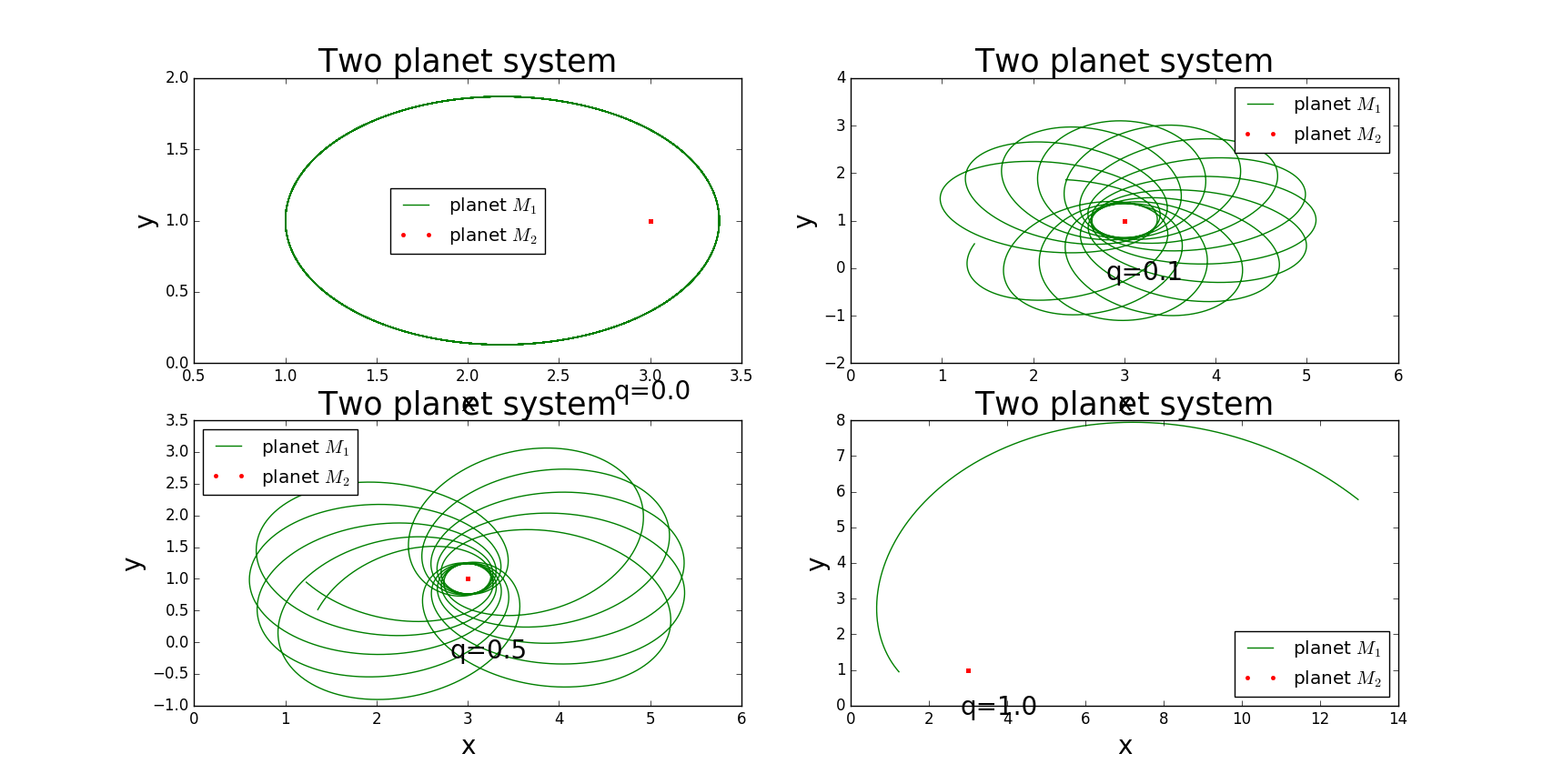
This is an unstable example here.

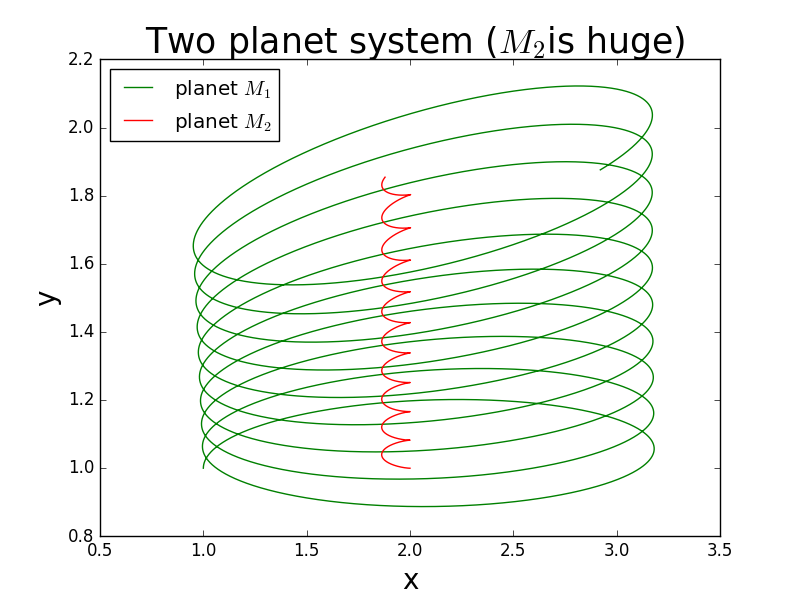
This picture is when the gravity is not inverse the distance's square. I creat the force is ralative with both $M_1$and$M_2$.And it's a little eccentric.

This passage is a little big .If it cannot appear.Here is a link :
https://raw.githubusercontent.com/yyfwhu/computationalphysics_N2013301020096/master/homework/picture/hw11_7.png

This is a special picture .I make a mistake here.But it's very beautiful .So I put it here .

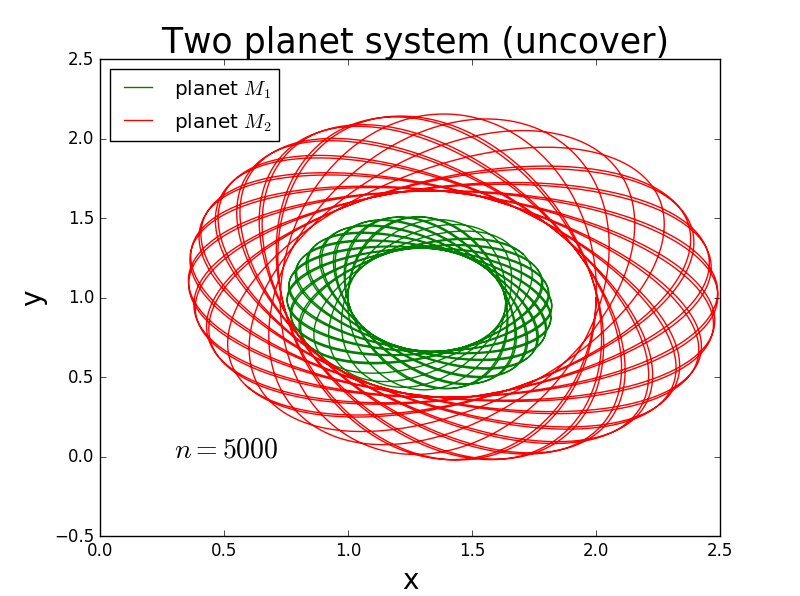
In this passage ,I first use the numpy to write the program. In numpy, it can use the vector. So it's very convenient.
Here is some of the codes:

class solar:
    def __init__(self, q = 0., et = 50,  m_1 = 4*pi , m_2 = 2*pi, pos_1 =array([1.,1.,0.]), pos_2 = array([3.,1.,0.]), v_1 = array([0.,1.,0.]), v_2 = array([0.,0.,0.]), dt = .0001 ):
        self.m_1 = m_1
        def update(self):
        print self.n
        for i in range(self.n):
            self.F_1 = self.m_1 * self.m_2 * (self.pos_2 - self.pos_1)/(inner(self.pos_1-self.pos_2, self.pos_1 - self.pos_2) ** ((3. + self.q) / 2.))
            self.F_2 = self.m_1 * self.m_2 * (self.pos_1 - self.pos_2)/(inner(self.pos_1-self.pos_2, self.pos_1 - self.pos_2) ** ((3. + self.q) / 2.))
            self.a_1 = self.F_1/self.m_1
            self.a_2 = self.F_2/self.m_2
            self.v_1 +=self.a_1 * self.dt
            self.v_2 +=self.a_2 * self.dt
            self.pos_1 +=self.v_1 * self.dt
            self.pos_2 +=0
            self.x_1.append(self.pos_1[0])
            self.y_1.append(self.pos_1[1])
            self.z_1.append(self.pos_1[2])
            self.x_2.append(self.pos_2[0])
            self.y_2.append(self.pos_2[1])
            self.z_2.append(self.pos_2[2])

The total codes are here

Conclusion

We can find from the above .It's hard for the two planets to be stable .And if the q is equal to 0.The system cannot be stable.But here are also some probelems. When we make one planet be still. It cannot be true in the reality world.So here is in some degree approximation.

Reference

• The intresting website of gravity
• The numpy documents
• wikipedia