homework10(Lorenz Model)

作业

---

name:姚逸飞
student number：2013301020096

Homework

• $\Bbb homework\; L:$Lorenz Model

Abstract

The Lorenz system is a system of ordinary differential equations (the Lorenz equations, note it is not Lorentz) first studied by Edward Lorenz. It is notable for having chaotic solutions for certain parameter values and initial conditions. In particular, the Lorenz attractor is a set of chaotic solutions of the Lorenz system which, when plotted, resemble a butterfly or figure eight.
————by wikipedia

Passage

In this passage will still discuss about the famous and distinct chaos:
Lorenz model.
From the text book ,we can get the equation as follow:

$$\begin{cases} \frac{{\rm d}x}{{\rm d}t}=\sigma(y-x) \\[2ex] \frac{{\rm d}y}{{\rm d}t}=-xz+rx-y \\[2ex] \frac{{\rm d}z}{{\rm d}t}=xy-bz \end{cases}$$
To simple the equation ,we usually take the$\sigma=10$,and $b=\frac{8}{3}$.Here $x$ is the temperature ,$y$ is the density of the liquid, and $z$ is the velocity of the liquid.
We still use the **Euler-Cromer Method**to caculate this equation.
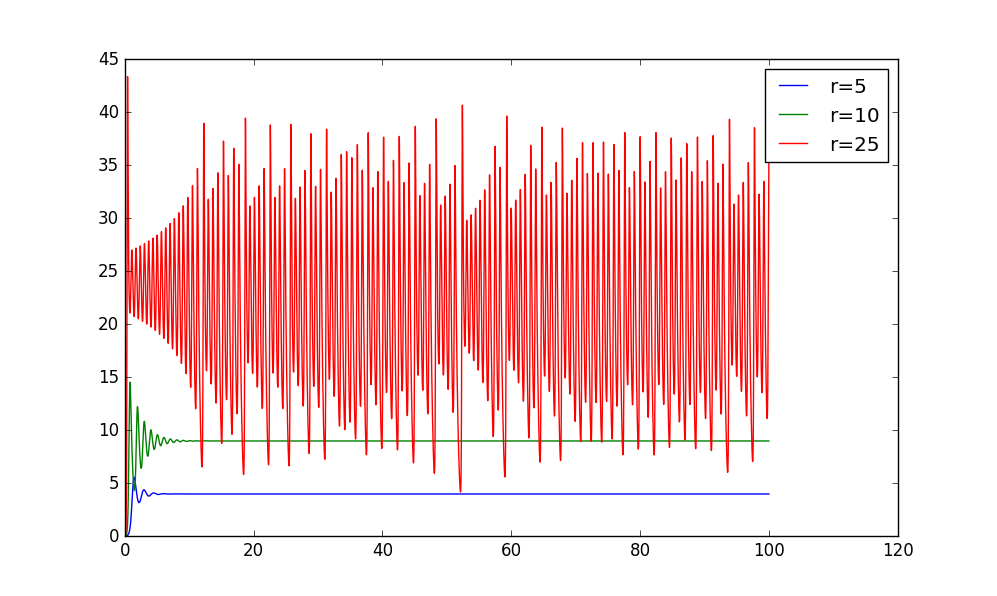
First we caculate the Z versus t,and see the case of the oscillation.Here $r=5$,$r=10$,$r=25$.

class lorenze:
    def __init__(self, r = 5,et = 0.01,  x = 1, y = 0, z = 0, dt = 0.01 ):
        self.x = [x]
        self.y = [y]
        self.z = [z]
        self.t = [0]
        self.r = r
        self.dt = dt
        self.et = et
        self.n = int(self.et / self.dt)
    def update(self):
        for i in range(self.n):
            self.t.append(self.t[-1] + self.dt)
            self.x.append(self.x[-1] + sig * (self.y[-1] -self.x[-1]) * self.dt)
            self.y.append(self.y[-1] + (-self.x[-1] * self.z[-1] + self.r * self.x[-1] - self.y[-1]) * self.dt)
            self.z.append(self.z[-1] + (self.x[-1] * self.y[-1] - b * self.z[-1]) * self.dt) 
    def plzt(self, pic):
        pic.plot(self.t, self.z, label = 'n=' + str(self.n))
        pic.legend(loc = 'best')
    def plzx(self, pic):
        pic.plot(self.x, self.z, '.', label ='r=' + str(self.r))
        pic.set_title('Z versus X')
        pic.legend(loc = 'best')
        pic.set_xlabel('X')
        pic.set_ylabel('Z')

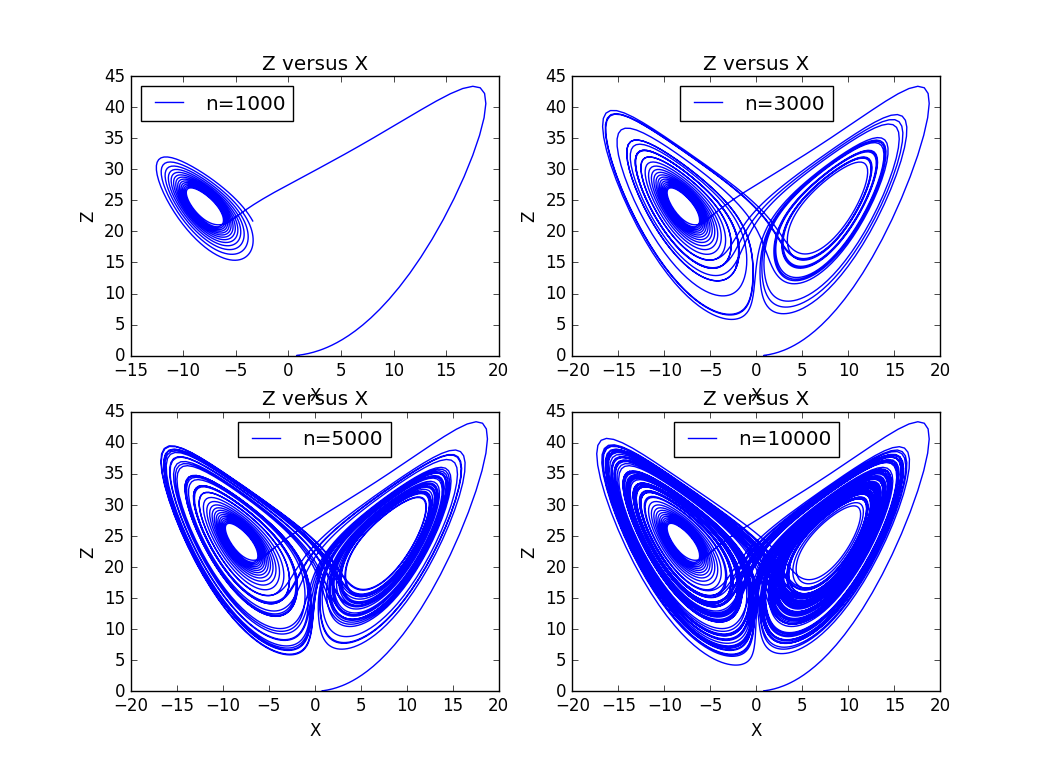
Then ,we will caculate the phase relation of the lorenz model.Here we first see the influence of different steps.n from 1000 to 10000.Here we choose the $r=29$.And z versus x.



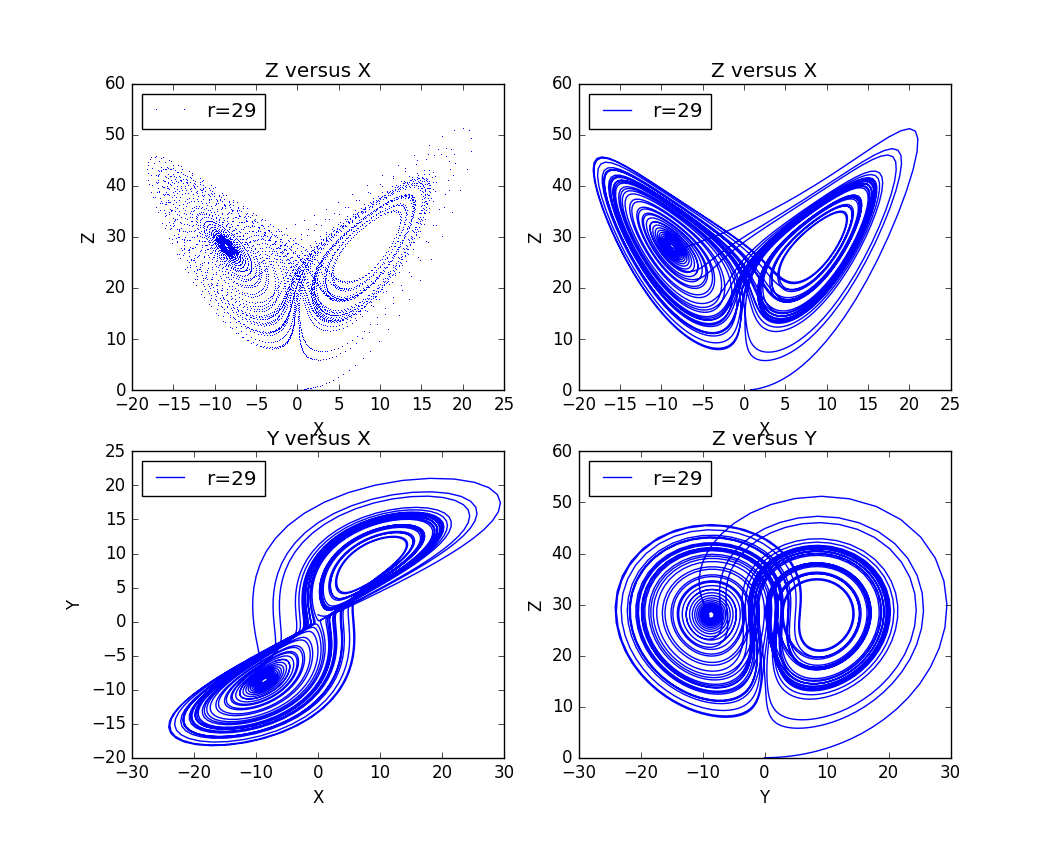
for further discussion, we put the picture in the phase space .And here we choose the z-y,z-x,and y-x.
And $r = 29$.We can see the chaos from different way.



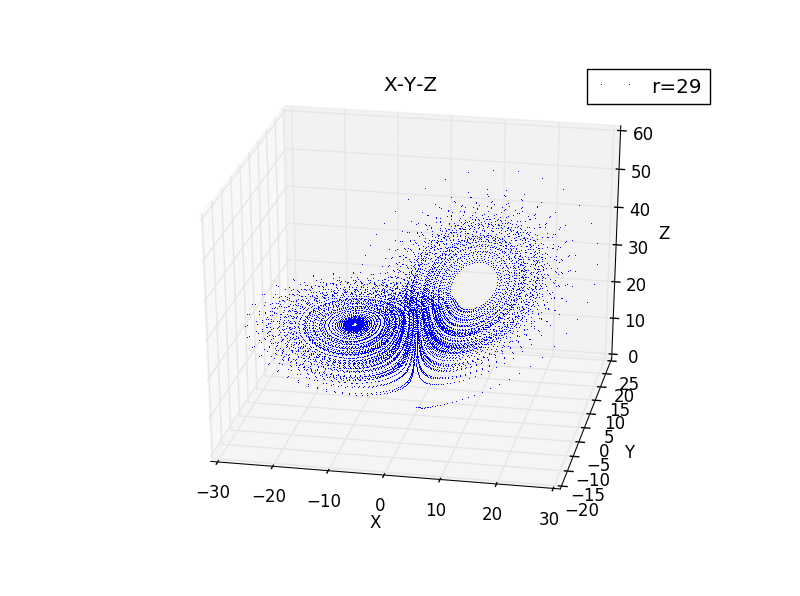
At last ,we plot the lorenz model in the 3-D space. it's prominently beautiful.



And the total code is Here

Conclusion

The lorenz model is classic and easy.But it's a very good example to stuy the chaos .But I didn't discuss r in different range. And the picture is doll in some degree.

Reference

• Text Book(of course)
• The 3-D picture matplotlib
• Lorenz model in wikipedia