Homework 9(chaos pendulum)

作业

name:姚逸飞
student number：2013301020096

Homework

• $\Bbb homework\; L1:$ 3.12
• $\Bbb homework\; L1:$ 3.16, 3.21

Abstract

This passage is mainly discuss about the chaos pendulum.
The chaos phenomenon are very general in physics.But it dosen't mean that it's very easy to make a system to be chaos.So this pasage mainly discuss about how to creat a chaos system.And we can see that a chaos system needs very strict parameter.And we will run the pendulum as an example.We will try to see the pendulum in different driven force.

(Here is a beautiful picture of chaos system)

Passage

The last passage is mainly discussing about the simple pendulum .But in this passage, the loss of the system and the driven force will be considered.So we can get the equation as follows:

$$\frac{\rm{d^2}\theta}{{\rm d}t^2}=-\frac{g}{l}{\rm sin}\theta-q\frac{{\rm d}\theta}{{\rm d}t}+F_D{\rm sin}\Omega_D\theta$$
And it's easy to get the fake code:

• $\omega_{i+1}=\omega_{i}-[(g/l){\rm sin}\theta_i+q\omega_i-F_D{\rm sin}\Omega_D\theta]\Delta t$
• $\theta_{i+1}=\theta_i+\omega_{i+1}\Delta t$
• If $\theta_{i+1}$ isout of the range $[-\pi,\pi]$,add or substract $2\pi$ to keep it in this range.
• $t_{i+1}=t_{i}+\Delta t$
  This program is very like the last one (simple pendulum) And the different is we should add the driven force and the loss

for i in range(self.n):
            if self.theta[-1] > pi:
                self.theta[-1] += -2 * pi
            elif self.theta[-1] < -pi:
                self.theta[-1] += 2 * pi
            self.t.append(self.t[-1] + self.dt)
            self.omg.append(self.omg[-1] - ( (self.g / self.l) * sin(self.theta[-1]) + self.q * self.omg[-1] - self.F * sin(self.omgd * self.t[-1]) ) * self.dt)
            self.theta.append(self.theta[-1] + self.omg[-1] * self.dt)
            if (self.omgd * self.t[-1] % (2 * pi)) / pi <= 0.01:
                self.sp_t.append(self.t[-2])
                self.sp_theta.append(self.theta[-2])
                self.sp_omg.append(self.omg[-2])         
            else:
                pass

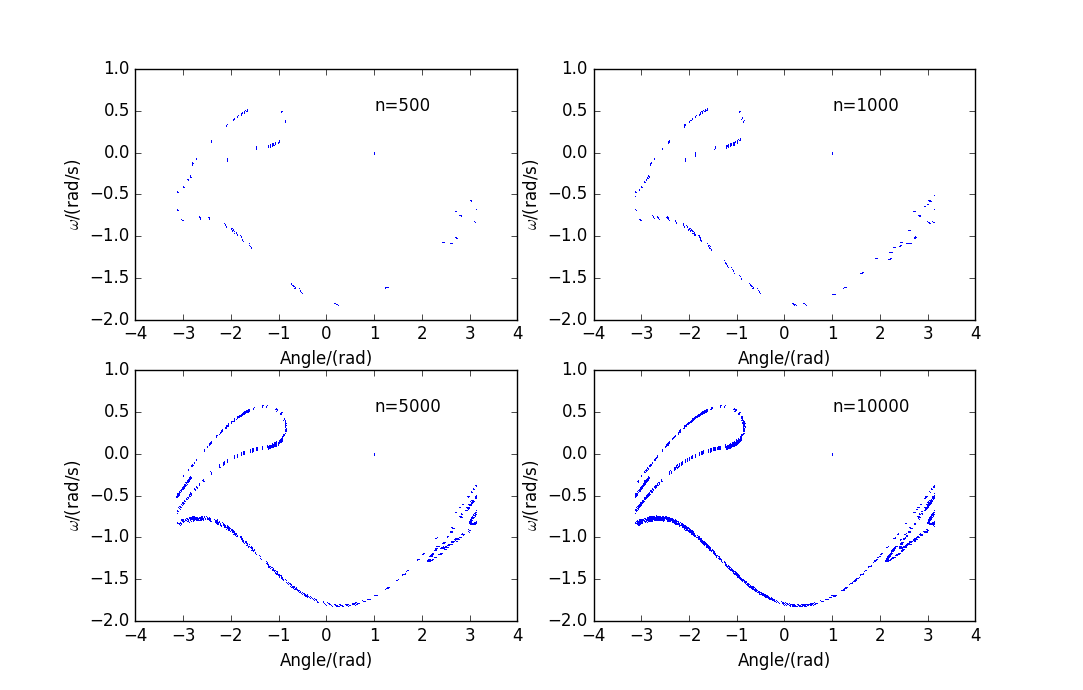
These picture are in different steps :

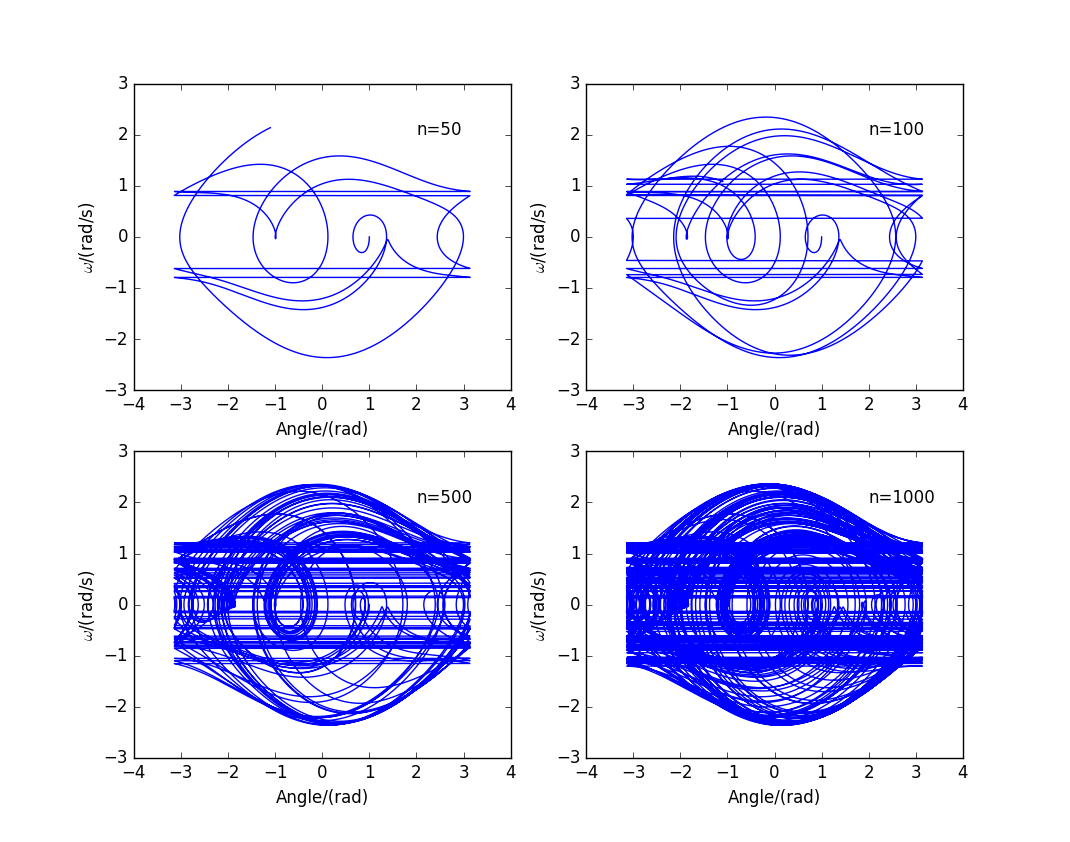
When $\Omega_Dt=2n\pi$,we can get the branches.
But it's hard for the euation to be strict,So in the program ,I use the different method. When $\Omega_Dt/\pi$ is very small,we can say the equation is right.The code is as follows:

 if (self.omgd * self.t[-1] % (2 * pi)) / pi <= 0.01:
   self.sp_t.append(self.t[-2])
                self.sp_theta.append(self.theta[-2])
                self.sp_omg.append(self.omg[-2])         
            else:
                pass

The total code is Here

Conclusion

We can see it must in $q=0.5$ and$F_D=1.2$,the system can become chaos.
So we should try some different parameters to achieve the best parameters.

Reference

• Thanks for the Cmd Markdown: https://www.zybuluo.com/codeep/note/163962#9