Exercise_10: The solar system

Abstract

From this charpter, we learn the problem of Kepler's Laws. And with the help of the Kepler's Laws, first we can solve the motion of the simplest situation where a sun and a single planet get moved with interaction. We investigate a few of the properities of this model solar system. Additionally,the inverse-square law and the stability of plantery orbits will be discussed. Then we can learn the precession of the perihelion of Mercury and we can try to plot the figure of the precession of perihelion of Mercury to have a better learning. Also, just like the better we use the Euler-Cromer method to solve the trobule of the precession of perihelion of Mercury.

background

There are many different situations in the study of planetary motion. Now consider a hypothetical, ideal celestial system consisting of two planets. Both experience only the gravitation produced by the other one.A few of the properties are investigated here.
For simplicity, the rest frame and the initial Center-of-Mass frame can be constracted in this way:for the rest frame, the x-axis is the line connecting both planet, while the y-axis is perpendicular to the x-axis from the point of center of mass. Besides, the Center-of-Mass frame in the beginning coincides with the rest frame.

main body

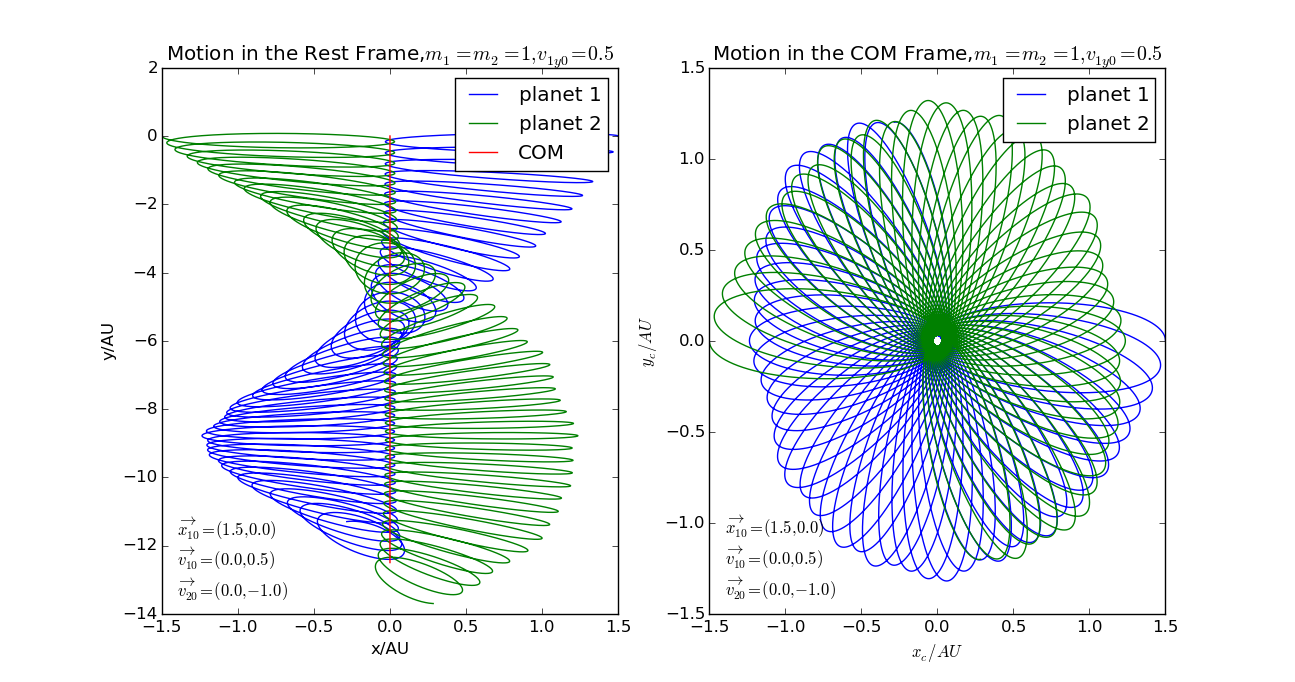
The motion in the REST FRAME is:

The motion in the COM FRAME is:

acknowledgement

codecogs
Computational Physics, Nicholas J. Giordano & Hisao Nakanishi