Exercise04

Abstract

• use python to do homework 1.5

Background

• After learning how to use Matplotlib and the first numerical problem, we start to solve a physics problem by our own.

Consider again a decay problem with two types of nuclei A and B, but now suppose that nuclei of type A decay into ones of type B, while nuclei of type B decay into ones of type A. Strictly speaking, this is not a "decay" process, since it is possible for the type B nuclei to turn back into type A nuclei. A better analogy would be a resonance in which a system can tunnel or move back and forth between two states A and B which have equal energies. The corresponding rate equations are

$$\frac{dN_A}{dt} = \frac{N_B}{\tau} - \frac{N_A}{\tau}$$
$$\frac{dN_B}{dt} = \frac{N_A}{\tau} - \frac{N_B}{\tau}$$

where for simplicity we have assumed that the two types of decay are characterized by the same time constant, $\tau$. Solve this system of equations for the numbers of nuclei, $N_A$ and $N_B$ , as functions of time. Consider different initial conditions, such as, $N_A=100$ , $N_B=0$ , etc., and take $\tau=1s$. Show that your numerical results are consistent with the idea that the system reaches a steady state in which $N_A$and $N_B$ are constant. In such a steady state, the time derivatives $dN_A/dt$ and $dN_B/dt$ should vanish.

The Main Body

import pylab as pl
class uranium_decay:
    def __init__(self, number_of_NA = 100,number_of_NB=0,time_constant = 1, time_of_duration = 5, time_step = 0.05):
        self.na_uranium = [number_of_NA]
        self.nb_uranium = [number_of_NB]
        self.t = [0]
        self.tau = time_constant
        self.dt = time_step
        self.time = time_of_duration
        self.nsteps = int(time_of_duration // time_step + 1)
        print "Initial number of NA ->", number_of_NA
        print "Initial number of NB ->", number_of_NB
        print "Time constant ->", time_constant
        print "time step -> ", time_step
        print "total time -> ", time_of_duration
    def calculate(self):
        for i in range(self.nsteps):
            tmpa = self.na_uranium[i] + (self.nb_uranium[i] - self.na_uranium[i])/self.tau * self.dt
            tmpb = self.nb_uranium[i] + (self.na_uranium[i] - self.nb_uranium[i])/self.tau * self.dt
            self.na_uranium.append(tmpa)
            self.nb_uranium.append(tmpb)
            self.t.append(self.t[i] + self.dt)
    def show_results(self):
        pl.plot(self.t, self.na_uranium)
        pl.plot(self.t, self.nb_uranium,'r')
        pl.xlabel('time ($s$)')
        pl.ylabel('Number of Nuclei')
        pl.show()
a = uranium_decay()
a.calculate()
a.show_results()

Conclusion

show result：

Initial number of NA -> 100
Initial number of NB -> 0
Time constant -> 1
time step ->  0.05
total time ->  5

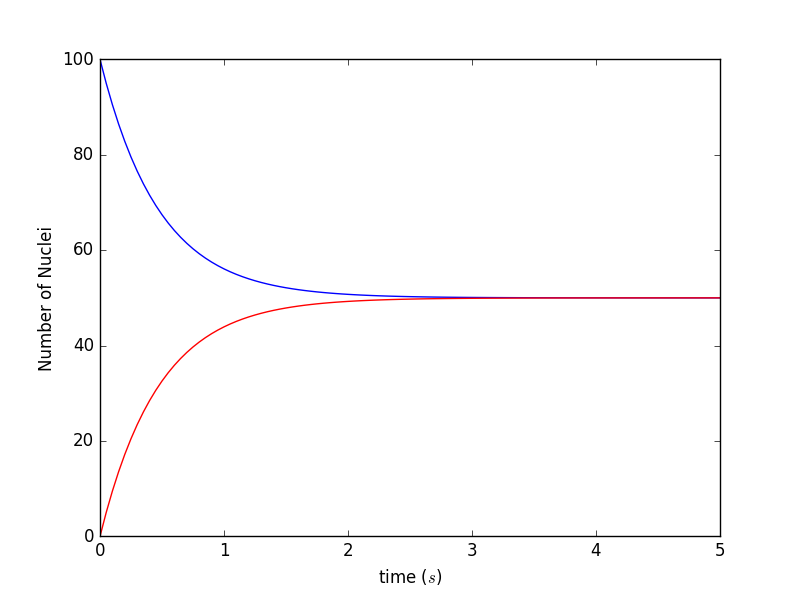
• Programming is a complex job, only little error can make a big problem.

Acknowledgment

• Thanks teacher cai's ppt and classmate Lijinting to guide me.