Exercise_06： The Trajectory of a Cannon Shell（2）

Abstract

• use python to do homework 2.10
• add the air resistance and the wind velocity

Background

• Genenralize the program developed for the previous problem so that it can deal with situations in which the target is at a different altitude than the cannon.Consider cases in which the target is higher and lower than the cannon.Also investigate how the minimum firing velocity required to hit the target varies as the altitude of the target is varied.(consider the wind velocity)

Main body

First considering the wind velosity

import pylab as pl
from math import *
class cannon:
    def __init__(self,init_v=100,B_m=0.00004,theta = 60,
                 init_x=0,init_y=0,time_step=0.1,wind_velocity=-10):     
        self.vx = [init_v*cos(theta*2*pi/360)]
        self.vy = [init_v*sin(theta*2*pi/360)]
        self.x = [init_x]
        self.y = [init_y]
        self.t = [0]
        self.B_m = B_m
        self.win = wind_velocity
        self.dt = time_step        
    def run(self):
        while self.y[-1]>=0:
            self.x.append(self.x[-1] + self.dt * self.vx[-1])
            self.y.append(self.y[-1] + self.dt * self.vy[-1])
            f=sqrt((self.vx[-1]-self.win)**2+self.vy[-1]**2) * self.B_m
            self.vx.append(self.vx[-1] - self.dt * f *(self.vx[-1]-self.win))
            self.vy.append(self.vy[-1] - self.dt * (9.8 + f *self.vy[-1]))
    def show_results(self):
        pl.plot(self.x, self.y,color="black",
                linestyle="-.",label="headwind")
        pl.xlabel('x(m)')
        pl.ylabel('y(m)')
        pl.legend(loc='upper right')
        pl.ylim(0)
        pl.show()
a = cannon()
a.run()
a.show_results()

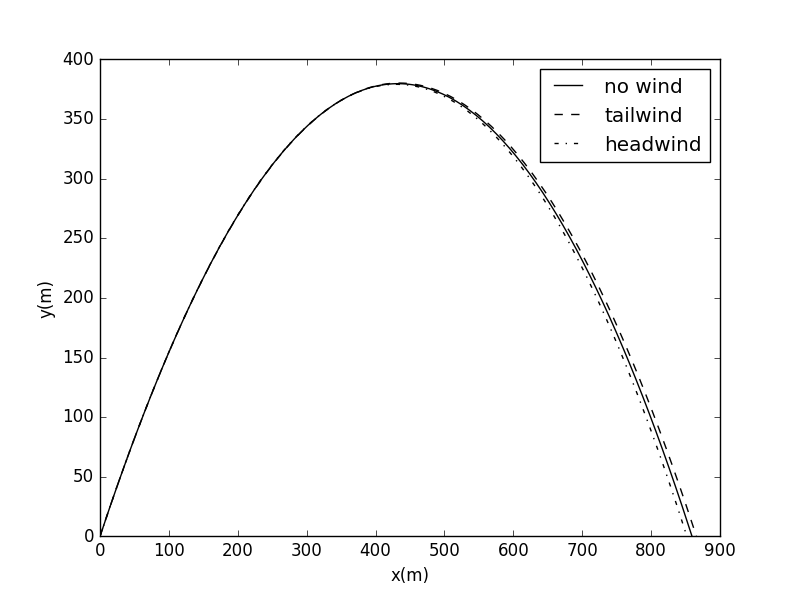
Then considering the altitude and height
when height =-100:
code:

import pylab as pl
import math 
class cannon:
    def __init__(self,init_v=100,B_m=0.00004,theta = 35,
                 init_x=0,init_y=0,time_step=0.1,wind_velocity=10,
                 a_0=0.0065, alpha_0=2.5, temp_0=298.0,height=-100):    
        self.vx = [init_v*math.cos(theta*2*math.pi/360)]
        self.vy = [init_v*math.sin(theta*2*math.pi/360)]
        self.x = [init_x]
        self.y = [init_y]
        self.t = [0]
        self.B_m = B_m
        self.a =a_0
        self.alpha=alpha_0
        self.temp=temp_0
        self.win = wind_velocity
        self.height=height
        self.dt = time_step        
    def run(self):
        while self.y[-1]>=self.height:
            self.x.append(self.x[-1] + self.dt * self.vx[-1])
            self.y.append(self.y[-1] + self.dt * self.vy[-1])
            rho = (1- self.a *self.y[-1]/  self.temp ) ** self.alpha
            f=math.sqrt((self.vx[-1]-self.win)**2+self.vy[-1]**2) * self.B_m * rho
            self.vx.append(self.vx[-1] - self.dt * f *(self.vx[-1]-self.win))
            self.vy.append(self.vy[-1] - self.dt * (9.8 + f *self.vy[-1]))
    def show_results(self):
        pl.plot(self.x, self.y,color="blue",
                linestyle="-", label="35")
        pl.xlabel('x(m)')
        pl.ylabel('y(m)')
        pl.legend(loc='upper right')
        pl.ylim(-100)
        pl.show()
a = cannon()
a.run()
a.show_results()

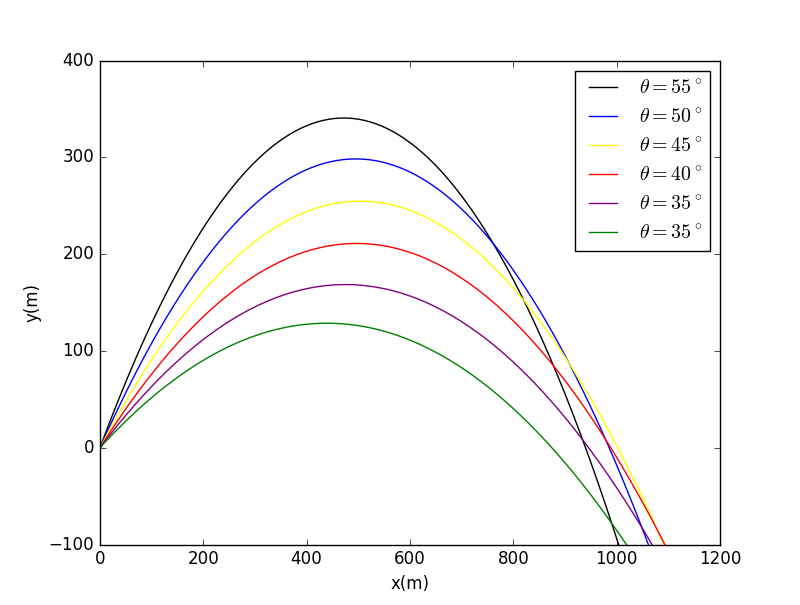
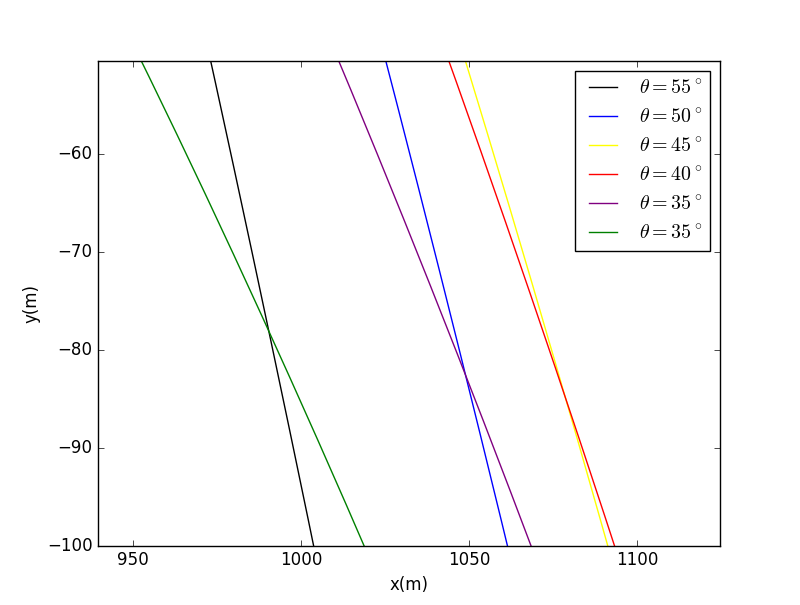
when height =100m:

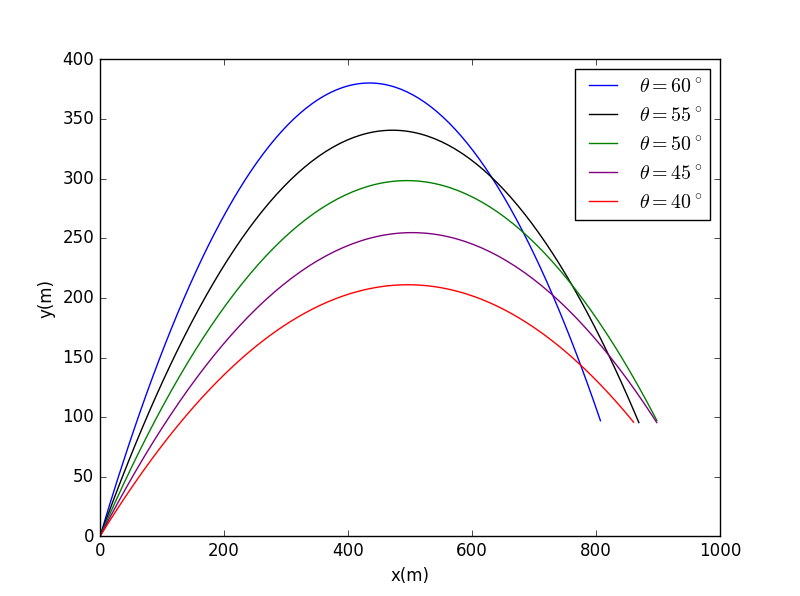
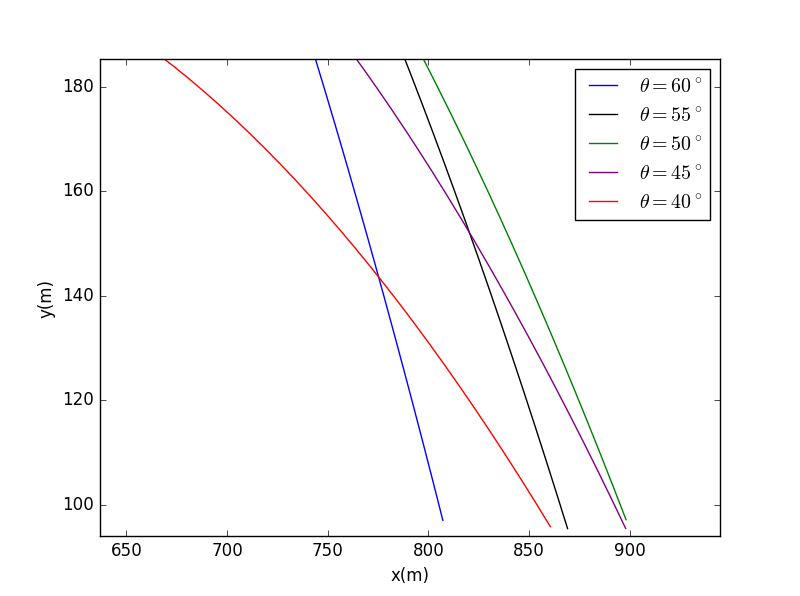
Conclusion

• From the picture, we can easily see that when height is -100, it is $\theta=40°$ that the farthermost the cannon hit,a little smaller than 45°. And when the heigtt is 100,$\theta=50°$ hit the farthermost, a little biger than 45°.
• Adding some realistic factor make the code more comflex, but the model will be more accurate

Acknowledgement

• Thanks to teacher cai's ppt.