概率题及智力题

面试

http://www.acmerblog.com/interviews-about-probability-5359.html
注意期望、方差公式以及贝叶斯定理~
数学期望中的递归:http://blog.csdn.net/pure_life/article/details/8100984

1. 三只骰子掷出10概率多少？
   解法1：
   共有6*6*6=216种
   结果分两类（1）1，3，6 1，4，5 2，3，5
   共有3*3！=18种结果
   （2）2，2，6 2，4，4 3，3，4
   共有3*3=9中结果
   18+9=27
   所以总概率为27/216=1/8=0.125
   解法2：
   利用隔板法，把10看成10个苹果，之间共有9个间隙，我们需要在这些间隙中插入2个隔板，从而生成3个骰子的数字
   0 0 0 0 0 0 0 0 0 0
   （1） 在第一个间隙位置插入隔板，这样第二个隔板智能插在4,5,6,7四个位置，共有4种
   （2） 在第二个间隙位置插入隔板，这样第二个隔板智能插在4,5,6,7,8五个位置，共有5种
   （3） 在第三个间隙位置插入隔板，这样第二个隔板智能插在4,5,6,7,8,9六个位置，共有6种
   （4） 在第四个间隙位置插入隔板，这样第二个隔板智能插在剩下的五个位置，共有5种
   （5） 在第五个间隙位置插入隔板，这样第二个隔板智能插在剩下的四个位置，共有4种
   （6） 在第六个间隙位置插入隔板，这样第二个隔板智能插在剩下的三个位置，共有3种
   共有 4+5+6+5+4+3=27种

0000-9999中6的数，按照概率很好算。。

扔骰子，1-2对方赢，3-5 自己赢，6重新仍，问自己赢的概率

有一个不规则的硬币 如何用它做一个1到6的随机数生成器 (找6个概率相同的事件)

斗地主摸到王炸和4个二的概率是多少
https://www.zhihu.com/question/28115076

置信区间？

如何通过3L和5L的水构造N升的水？
N=4L的时候
将5L倒满，用5L往3L倒满（此时5L剩2L），将3L杯子水倒掉，将5L中剩余的2L水倒入3L中，将5L倒满（此时3L杯中有2L水），用5L向3L倒把3L倒满，5L杯子内的水就是4L。我说完面试官又问我如果反过来倒呢？这个其实也简单，大家可以思考一下。

田忌赛马
https://blog.csdn.net/guoxuequan/article/details/6766574
https://blog.csdn.net/guoxuequan/article/details/8048657

一个人在沙漠中抛锚了，已知每天有车经过的概率是60%,问他在前8个小时获救的概率是多少？

题目： 一个骰子， 6 面， 1 个面是 1 ， 2 个面是 2 ， 3 个面是 3 ， 问平均掷多少次能使 1 、 2 、 3 都至少出现一次。

方法： 面对面试概率题几乎屡试不爽的分叉树递归列方程法。

这是一个求数学期望的问题，最终是求 1 ， 2 ， 3 出现至少一次的最短长度的期望。

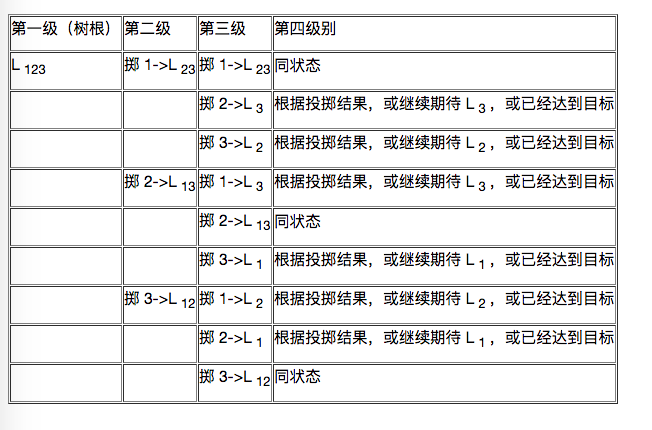
这样分叉树的每个节点是一个期望状态，而每个分叉是一次投掷结果。将后续期望出现 1 、 2 、 3 各至少一次的情形记作 L 123 （即题目所求），将后续期望出现 1 、 2 各至少一次（ 3 无关）情形记作 L 12 ，而 1 至少一次（ 2 ， 3 无关）情形 L 1 ，其余数值符号类推，则树结构如下（列出 4 级结构已经足够）：

接下来，就是要排出方程，因为一共 7 个未知数，如果排出 7 个线性方程就能解决问题。

这方程组里的未知数对应上述的状态，而其数值则是一个对长度（投掷次数）的数学期望。

根据这个树状结构和其中的递归关系，这个方程组就是：

L 123 = p 1 (L 23 + 1) + p 2 (L 13 +1) + p 3 (L 12 + 1) = p 1 L 23 + p 2 L 13 + p 3 L 12 + 1

（以这个 L 123 为例，解释，投掷 1 的概率是 p 1 而由此得到的结果是需要期待后续 2 和 3 各至少出现一次，于是长度期望是 L 23 + 1 ，加 1 是因为投掷了一次，亦即即增进一级）

L 23 = p 1 L 23 + p 2 L 3 + p 3 L 2 + 1

L 13 = p 1 L 3 + p 2 L 13 + p 3 L 1 + 1

L 12 = p 1 L 2 + p 2 L 1 + p 3 L 12 + 1

L 1 = p 1 + p 2 L 1 + p 3 L 1 + 1

（这里实际上是 L 1 =p 1 ·1 + p 2 (L 1 + 1) + p 3 (L 1 + 1) = p 2 L 1 + p 3 L 1 + 1 ，因为对 L 1 情形，如果投了 1 就目的达到终止了）

L 2 = p 2 + p 1 L 2 + p 3 L 2 + 1

L 3 = p 3 + p 1 L 3 + p 2 L 3 + 1

（以上一开始没注意，多加了悬空的概率项，故计算有误）

其中 p 1 ， p 2 和 p 3 分别是掷出 1 ， 2 和 3 的概率，即 1/6 ， 1/3 ， 1/2 。

于是求解这个方程，得到：

L 1 = 6 ， L 2 = 3 ， L 3 = 2

L 12 = 7 ， L 13 = 13/2 ， L 23 = 19/5 6

L 123 = 219/30 = 7.3 259/36 ~= 7.14

故以上如果没有计算错误，该题结果是，平均掷 7.3 约 7.14 次可出现这些面值各至少一次。

【另一解法】感谢 4 楼 aaaxingruiaaa 同学提供的答案（指示器变量法），整理如下：

定义随机变量 X n ，其可能值为 0 或 1 ，其值为 1 表示 “ 前 n 次掷骰子， 1 ， 2 ， 3 没能都至少出现一次 ” 的事件，其值为 0 表示这个事件没有发生，即 “ 前 n 次掷骰子， 1 ， 2 ， 3 各至少出现一次 ” 。

令 p n 为 “ 掷 n 次骰子， 1 ， 2 ， 3 没能都至少出现一次 ” 的概率，所以显然 p n = Pr{ X n =1} ，于是 p n = 1·Pr{ X n =1} + 0·Pr{ X n =1} = E[ X n ] ，即这个随机变量的数学期望。

令随机变量 X 表示 1 ， 2 ， 3 刚好全部出现过需要的投掷次数。可见题目要求的就是 E[X] 。

关键等式： X = Sigma (n=0 to Inf; X n ) （这里 Sigma 是求和号，求和范围是 n 从 0 到无穷大）

说明一下，等式两边都是随机变量，假设对于某个随机实例（例如，这里指一次具体的投掷序列），其对应事件是： “ 投了 K 次恰好 1 ， 2 ， 3 都出现了 ” ，于是等式左边显然等于 K ；而等式右边，对于 n < K ，由于这些项的对应定义事件发生了（即 1 ， 2 ， 3 没能出现），所以他们的实例值是 1 ，而对于 n⩾K ，则由于对应定义事件都没发生，实例值为 0 ，可见这个和也是 K 。故两侧相等。（为了达到这个相等关系，可以看出需要把 X 0 包含在内的必要性）

值得注意的是（但对于解这道题也可以不去注意，但注意一下有利于比较深入地理解），对 n < 3 ， X n 显然恒为 1 。而对于 n⩾3 ，这些随机变量不是独立的。他们的相关性是不容易求出的，唯一容易知道的是，当序列中一个项为 0 时，其后的项均为 0 。好在对于这题我们不需要担忧这个相关性。

由于数学期望的加性与随机变量的相关性无关（这是数学期望一个很令人高兴的性质），所以即便这样， E[X] 也能容易求出：

E[X] = Sigma (n=0 to Inf; E[ X n ] ) = Sigma (n=0 to Inf; p n )

p n 的比较直观的求法也由 aaaxingruiaaa 同学 提供了，即所谓容斥原理。稍微解释一下，由于 p n 考虑的是 n 次投掷三者没有全部出现，于是就是其中两者出现或仅一者出现。假设单次投掷 1 ， 2 和 3 出现的概率分别为： r 1 ， r 2 和 r 3 。于是 ( r 1 + r 2 ) n 表征 n 次投掷只出现 1 或 2 的概率，这其中包括了出现全 1 和全 2 的情形，于是求 p n 可由这样的项求和并剔除重复计算的单面值情形，于是：

p n = ( r 1 + r 2 ) n + ( r 1 + r 3 ) n + ( r 2 + r 3 ) n - r 1 n - r 2 n - r 3 n ，当 n > 0 ； 而 p 0 = 1 （由定义；同时也可以检验看出，这个 p n 在 n 为 1 和 2 的时候都是 1 ）

于是由等比级数（等比数列求和）公式：

E[X] = 1 + Sigma (n=1 to Inf; ( r 1 + r 2 ) n + ( r 1 + r 3 ) n + ( r 2 + r 3 ) n - r 1 n - r 2 n - r 3 n = 1 + (1 - r 3 ) / r 3 + (1 - r 2 ) / r 2 + (1 - r 1 ) / r 1 - r 1 / (1 - r 1 ) - r 2 / (1 - r 2 ) - r 3 / (1 - r 3 ) = 7.3

【程序仿真】 http://m.nowcoder.com/discuss/1758

以下程序进行一千万轮投掷的仿真，结果基本在 7.3 周围。至此此题答案 7.3 毫无疑问了。

有三种颜色ABC的球分别若干，每个球除了颜色之外都一样，现在共取出100个，要求ABC三种颜色的球至少每类一个，求一共有多少种取法？谢谢

100个点，有99个缝隙，从99个缝隙里选2个位置会把这100个球分成三份，答案是C(99,2)

如果一个人在公路上半小时遇到车的概率是0.9，那么10分钟之内遇到汽车的概率的是多少？
设答案为x，则(1-x)^3=1-0.9求出答案即为x

两道概率题：
1. 一个人在沙漠中车抛锚了，已知每天有车经过的概率是60%，问他在前8个小时获救的概率是多少？
2. 扫雷游戏： 在一个局部的情形中，点开了1和2，X表示未知，问A,B,C,D中哪一点是雷的概率最大？
X X X X X
A 1 B 2 C
X X D X X

第二题：有一个GOD（）函数，能够以C的概率返回0，以1-C的概率返回1，C未知，让利用GOD（）构造P（x )实现以X的概率返回0,1-X的概率返回1，不能使用随机函数

给定一个能够生成0,1两个数的等概率随机数生成器”，如何生成⼀个产生0,1,2,3的等概率随机数生成器?
和上题类似，如何用rand7生成rand9?

答案:将两个0,1随机生成器级联，每次产生两个数，则可能的结果有(0,0), (0,1), (1,0), (1,1)，分别映 射到0, 1, 2, 3即可
两个rand7可以产生49种可能，扔掉后面的4种，保留前45个，并平均分成9份，每次产生一个结果时，假如没落在对应区间中就扔掉，否则根据落在哪个区间判断是0--8中哪个
拒绝采样的思想，类似:https://leetcode.com/problems/implement-rand10-using-rand7/solution/

如何等概率地从n个数中随机抽出m个数？
上题中如果n的大小不确定（可以认为是⼀个数据流），如何做？

答案:
https://www.nowcoder.com/questionTerminal/12796031452e4ced8a16255bb02c4168

整数数组的前m个直接存下来。
用一个计数器保存当前正在处理的请求是第几个，比如n
对于从m+1开始的新请求，以m/n的概率选择保存，并同从已保存的m个请求中随机选出的一个进行交换。
细说就是，

对于第m+1个请求，以m/(m+1)的概率选择留下，如果留下了则从已保存的m个请求中随机选出一个，同它交换;
对于第m+2个请求，以m/(m+2)的概率选择留下，如果留下了则从已保存的m个请求中随机选出一个，同它交换;
对于第m+3个请求，以m/(m+3)的概率选择留下，如果留下了则从已保存的m个请求中随机选出一个，同它交换;
…

对于第n个请求，以m/n的概率选择留下，如果留下了则从已保存的m个请求中随机选出一个，同它交换

一．最基本题型（说明：此类题型比较简单）
1.烧一根不均匀的绳，从头烧到尾总共需要1个小时。现在有若干条材质相同的绳子，问如何用烧绳的方法来计时一个小时十五分钟呢?

把第一根绳子两头同时点燃,同时把第二根绳子点燃一头,当第一根绳子烧完时,时间为半个小时,这时把第二根绳子的另一头也点燃,开始计时,当第二根绳子烧完时,停止计时,那么这段时间就是15分钟.

2.你有一桶果冻，其中有黄色、绿色、红色三种，闭上眼睛抓取同种颜色的两个。抓取多少个就可以确定你肯定有两个同一颜色的果冻？ 最多抓4个，鸽巢原理

3.如果你有无穷多的水，一个3公升的提捅，一个5公升的提捅，两只提捅形状上下都不均匀，问你如何才能准确称出4公升的水?

4.一个岔路口分别通向诚实国和说谎国。来了两个人，已知一个是诚实国的，另一个是说谎国的。诚实国永远说实话，说谎国永远说谎话。现在你要去说谎国，但不知道应该走哪条路，需要问这两个人。请问应该怎么问？

5.12个球一个天平，现知道只有一个和其它的重量不同，问怎样称才能用三次就找到那个球。13个呢？（注意此题并未说明那个球的重量是轻是重，所以需要仔细考虑）
12个球时的解法:
1，天平一边放四个，平则坏球在余下的四个里，好办（同方法二中的相等处理）。 不平，先将偏重的四个编号为：1、2、3、4。偏轻的编为A、B、C、D（因为不知道轻重）。
2。天平一边放三个，比如：左边放1、2、A。右边放3、4、B。 平则坏球是C、D 里偏轻的，不平则根据轻重淘汰1、2、B或 3、4、A。
假设是12A>34B，那么一定是12中有一个偏重或者B偏轻，最后一次把12B相称即可，假设称12，若相等则是B偏轻，否则谁重谁有问题。
反之亦然。

6.在9个点上画10条直线，要求每条直线上至少有三个点？

7.在一天的24小时之中，时钟的时针、分针和秒针完全重合在一起的时候有几次？都分别是什么时间？你怎样算出来的？

答案：
1.一要一头烧，一根从两头烧，再有一根做参照，两头烧完的记下位置（即烧到这里要半小时），把参照的那根从标记位置处剪开，取其中一段A。
一头烧的那根烧完后（就是一个小时后），把A从两头开始烧，烧完后即为十五分钟，加起来共一小时十五分钟。

2、四个

3.大桶装满水，倒入小桶，大桶剩下2公升水。小桶水倒掉，大桶剩2公升水倒入小桶中，大桶再装满后，倒入小桶至小桶满，大桶即剩４公升水。

4.如果参加过类似于奥林匹克数学班的，都应做过这些题。问他你的国家怎么走，他肯定指向的是诚实国。

5.12个时可以找出那个是重还是轻，13个时只能找出是哪个球，轻重不知。
把球编为①②③④⑤⑥⑦⑧⑨⑩⑾⑿。（13个时编号为⒀）
第一次称：先把①②③④与⑤⑥⑦⑧放天平两边，
㈠如相等，说明特别球在剩下4个球中。
把①⑨与⑩⑾作第二次称量，
⒈如相等，说明⑿特别，把①与⑿作第三次称量即可判断是⑿是重还是轻
⒉如①⑨＜⑩⑾说明要么是⑩⑾中有一个重的，要么⑨是轻的。
把⑩与⑾作第三次称量，如相等说明⑨轻，不等可找出谁是重球。
⒊如①⑨＞⑩⑾说明要么是⑩⑾中有一个轻的，要么⑨是重的。
把⑩与⑾作第三次称量，如相等说明⑨重，不等可找出谁是轻球。
㈡如左边＜右边，说明左边有轻的或右边有重的
把①②⑤与③④⑥做第二次称量
⒈如相等，说明⑦⑧中有一个重，把①与⑦作第三次称量即可判断是⑦与⑧中谁是重球
⒉如①②⑤＜③④⑥说明要么是①②中有一个轻的，要么⑥是重的。
把①与②作第三次称量，如相等说明⑥重，不等可找出谁是轻球。
⒊如①②⑤＞③④⑥说明要么是⑤是轻的，要么③④中有一个是重的。
把③与④作第三次称量，如相等说明⑤轻，不等可找出谁是重球。
㈢如左边＞右边，参照㈡相反进行。
当13个球时，第㈠步以后如下进行。
把①⑨与⑩⑾作第二次称量，
⒈如相等，说明⑿⒀特别，把①与⑿作第三次称量即可判断是⑿还是⒀特别，但判断不了轻重了。
⒉不等的情况参见第㈠步的⒉⒊
6. 见下面的点 10条线的情况是 123 456 789 148 159 247 258 269 357 368
①　②　③

④⑤⑥

⑦　⑧　⑨

7.首先考察时针与分针的情况，很容易看出分针转一圈与时针只重合一次，就是一小时一次。但11时与0时的分钟区内共享一个重合点，所只24

小时中，只有22次重合，现在只需考察这22个重合点时，秒针与不与它重合就行了（实际上，只要判断11个重合点，剩下的11个情况相同）。
0时整当然没问题，当n点到n+1点间(n=1,2,……10)，设这时是X小时
则30°X=60(X-n)ｘ6°
即X=12n/11。
此时时针分针的位置是30°X=(360/11)n°=(32+8/11)n°
秒针的位置是360(X-n)6°=(4320/11)n°=(392+8/11)n°=360n°+(32+8/11)n°=(32+8/11)n°
重合！所以共有22个点重合。

谷歌（电面 + 1轮onsite = 拿到了offer）
电面：只有自我介绍和一道算法题，保密协议而且题目简单，也没什么说的。注意和面试官多互动。
onsite：去了谷歌北京office，一道算法，工程方面也聊了3分钟。面试结果都是当天出，然后送审hc，一周后出结果。
微软（网测 + 3轮onsite = 拿到了offer）
网测：4道acm题400分，只拿到230，不过也过了。
onsite：微软北京office，3轮同一天，每轮大概45分钟。前2轮都是简单算法题，工程都不超过3分钟。最后1轮是项目boss面，1小时全程聊项目和人生。面试官都很nice，boss很看重potential。

1. 估算广州有多少辆车多少辆桥？每辆桥每天通车量是相同的么？
2. 海盗分金币问题-博弈论 http://wenku.baidu.com/view/12a64ed449649b6648d7472d.html
3. 一共1000瓶酒，其中一瓶有毒，利用10只老鼠判别出哪瓶酒有毒？http://zhidao.baidu.com/question/366396386.html
4. http://wenku.baidu.com/view/c772b6acd1f34693daef3ea7.html
5. http://download.csdn.net/download/gxw2008/596871
6. http://bbs.yingjiesheng.com/thread-18573-1-1.html

概率题，抛2k+1次硬币，问正面次数比背面多的概率是多大，并讲出数学证明思路。
假设正反面概率是1/2,那么抛2k+1次硬币就是一个伯努利分布(2k+1,1/2)
求正面比反面次数多的概率为P.
P=(1/2)^n*{C(2k+1,2k+1)+C(2k+1,2k)+C(2k+1,2k-1)+...C(2k+1,k+1)}=(1/2)^n*{C(2k+1,0)+C(2k+1,1)+..C(2k+1,k)}=(1/2)^n*(1/2){C(2k+1,0)+.....C(2k+1,2k+1)}
其中组合公式求和为2^n,所以上式为:
P=(1/2)^n(1/2)*(2^n)=1/2
这里n=2k+1