@cyy652415049
2016-05-31T04:30:56.000000Z
字数 1724
阅读 3751
计算物理第14次作业 Wave
作者:陈洋遥 学号2013301020169 更新时间:201605031
内容目录
本文摘要
波动现象是自然界十分常见的现象,从弹性波(例如绳波、水波等)到电磁波,再到引力波,波动现象是物理学研究的重要课题。解决波动问题,首先要建立波动方程,而后的问题就是在给定边界条件下求解波动方程。本次作业完成课后习题6.6,6.13,展示绳波的传播、反射过程,给出给定点振动的功率谱。
研究背景
绳波是一维波动问题,在不考虑能量损耗、认为绳是轻柔绳的前提下,绳波由如下波动方程描述:
其中是波速。要解出绳波的运动状态,必须给定一定的边界条件。常见的边界条件有自由边界条件和固定边界条件等。为简单起见,这里取固定边界条件,即绳端总是不发生横向位移。对于非端点的元段,则可以让其离散化,然后通过如下的迭代方法逐步求解绳波随时间的演化:
这里,和分别是时间和元段位置坐标。初始条件通过如下方法给出:在连续两个时刻,给出绳波位移,这样即可开始迭代,给出绳波随时间的演化。
绳波问题的求解
绳波随时间的演化
以一个高斯波包来描述绳波被激发时的形态,通过求解上面的波动方程,给出绳波的演化如下:
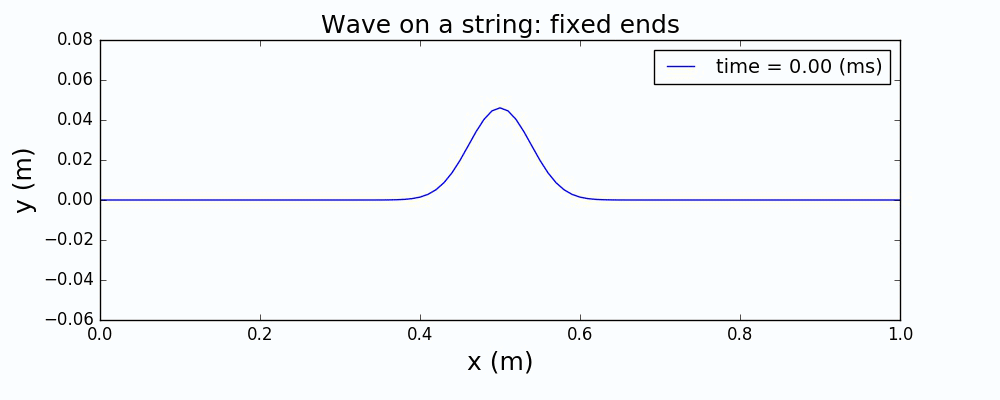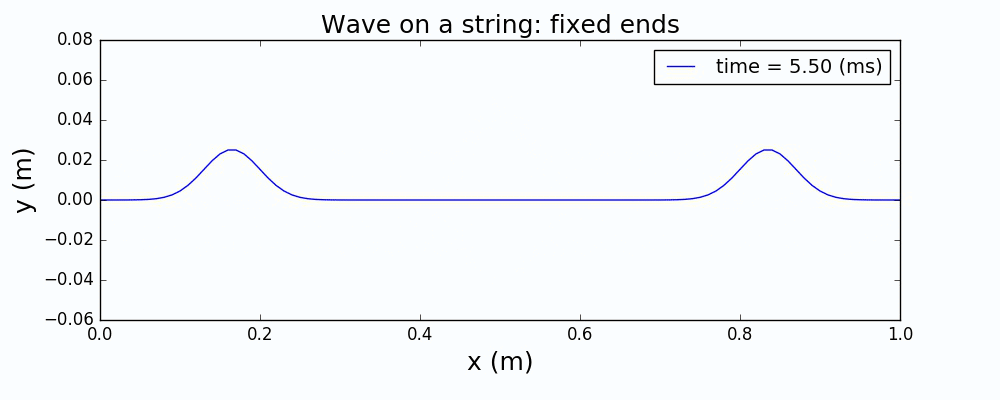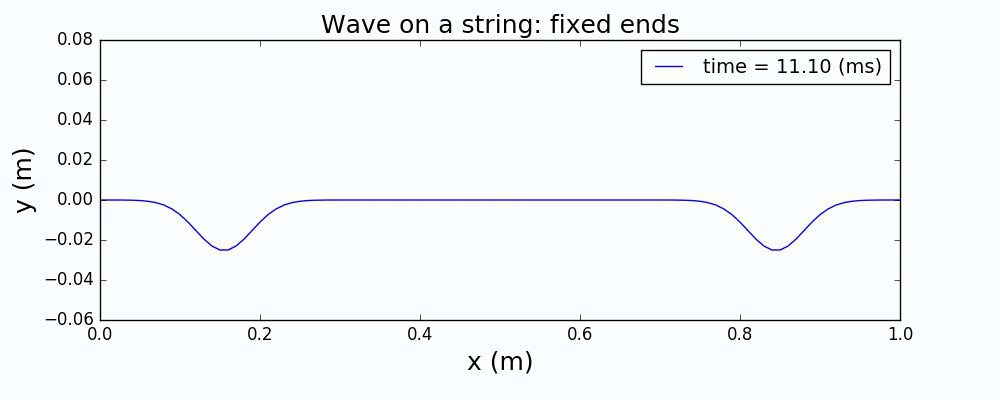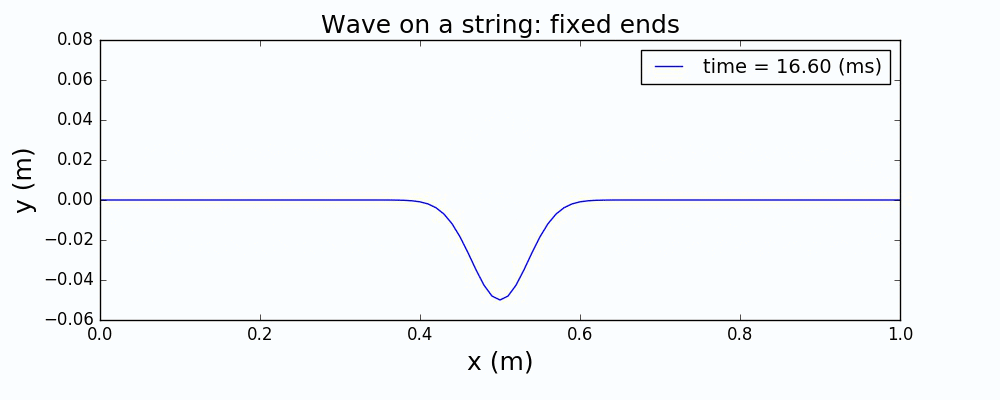
图1 中心激发高斯波包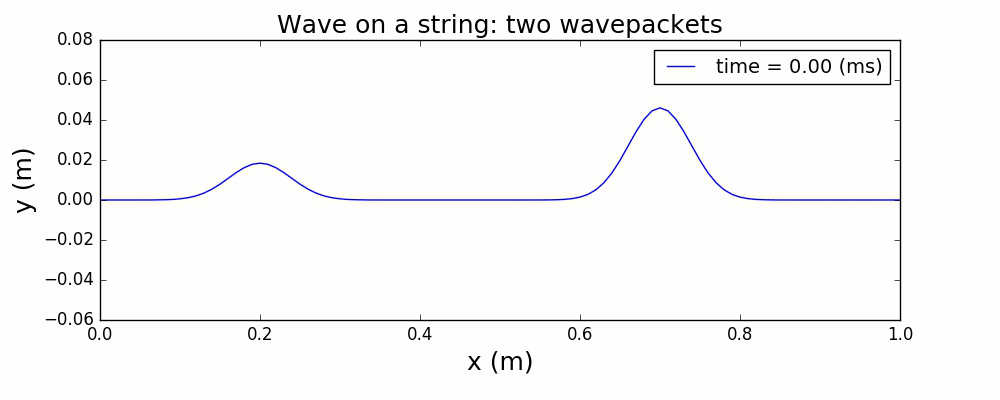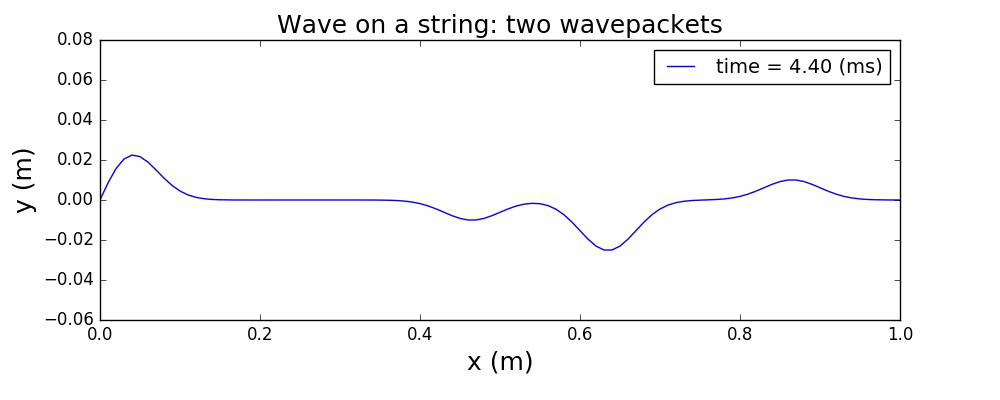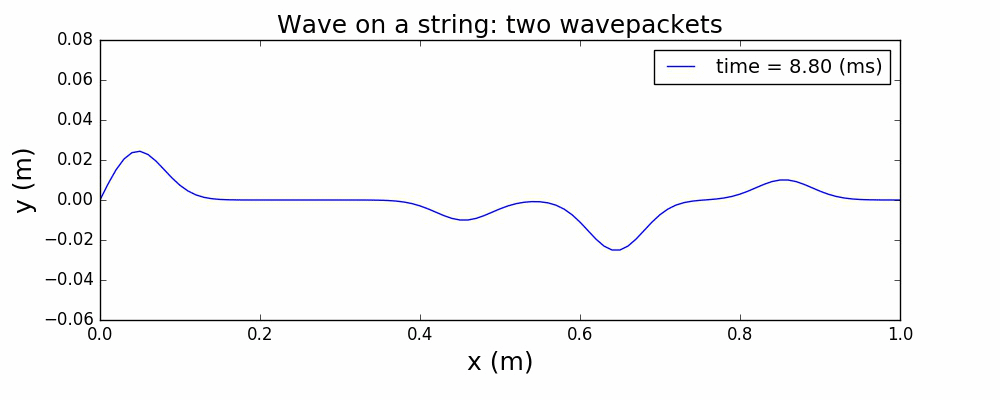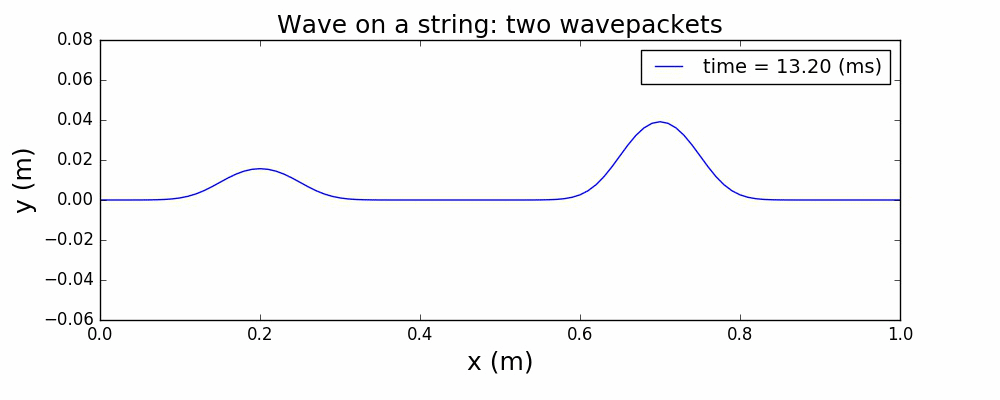
图2 两个高斯波包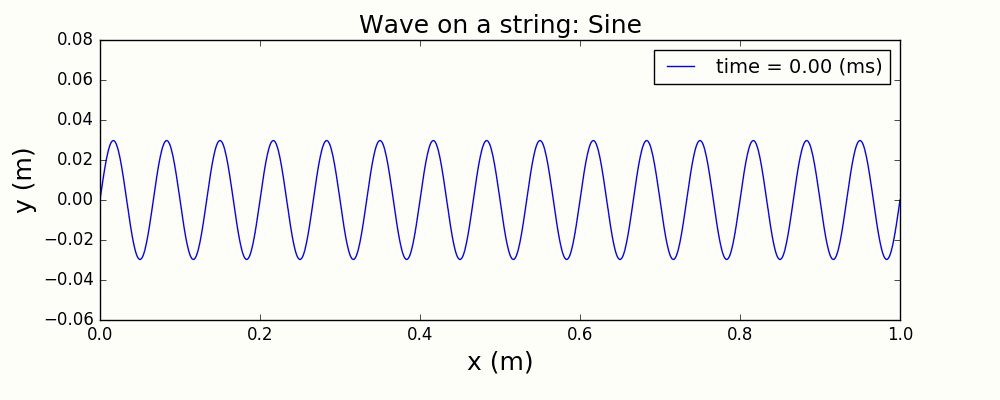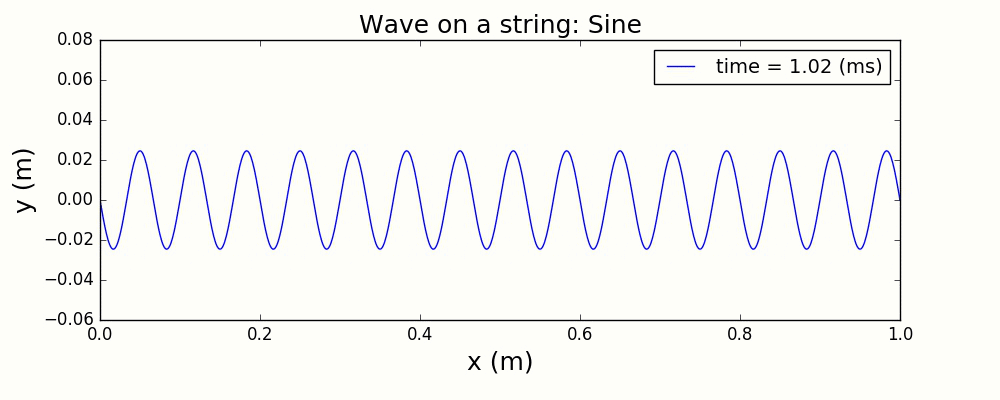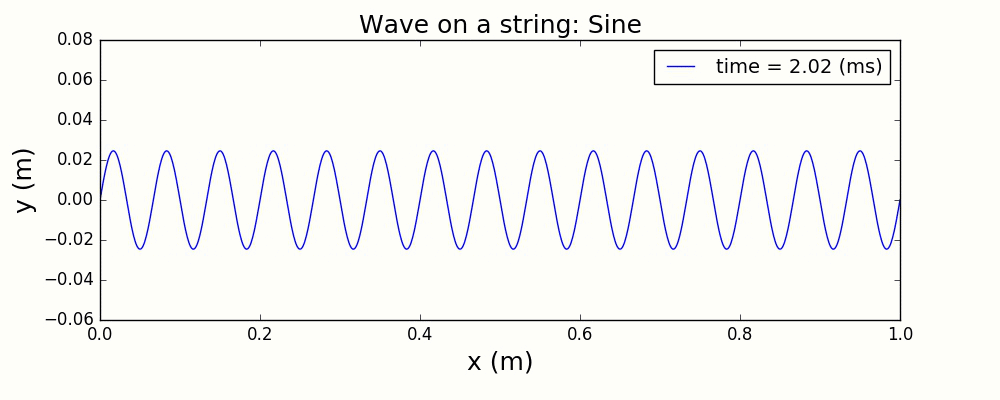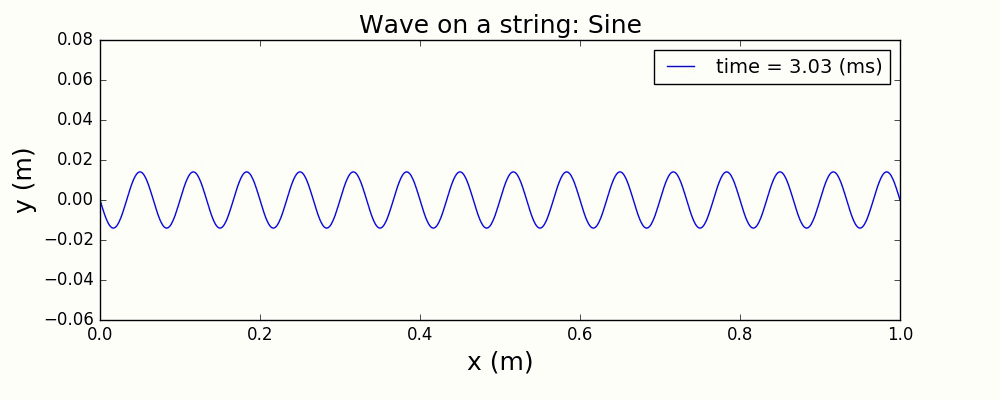
图3 正弦波激发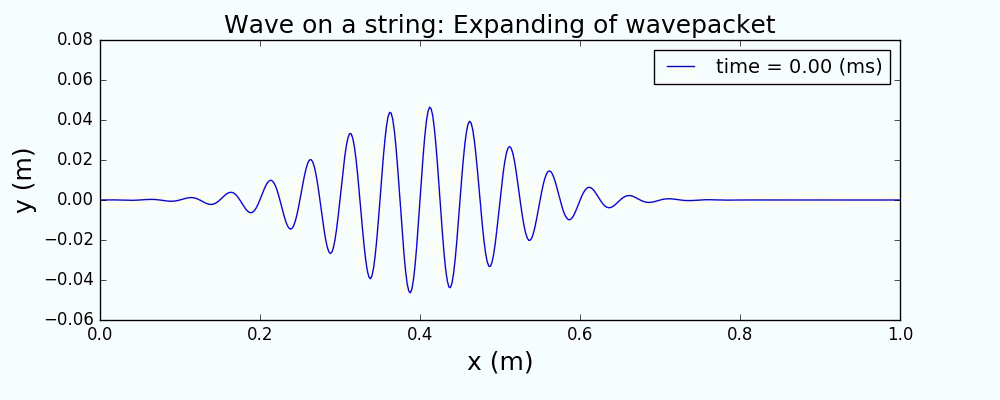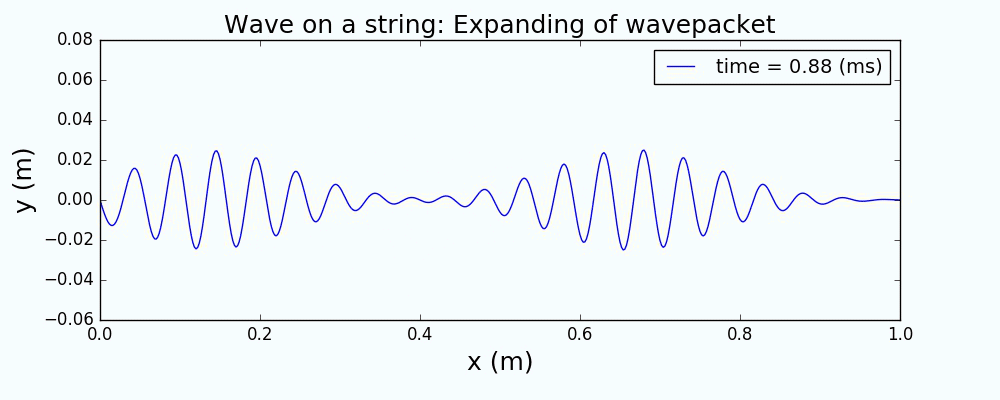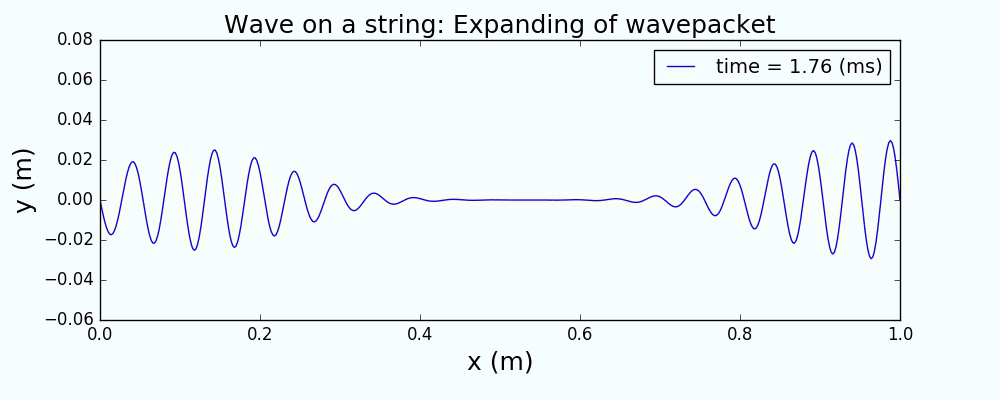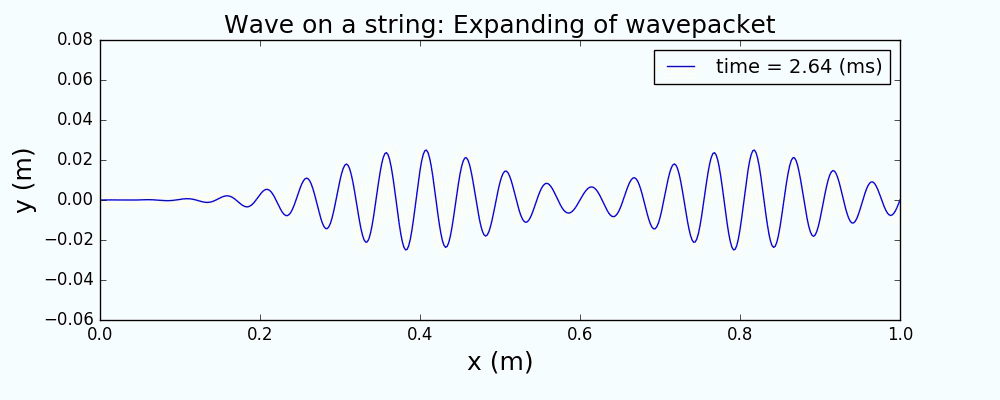
图4 正弦+高斯波包激发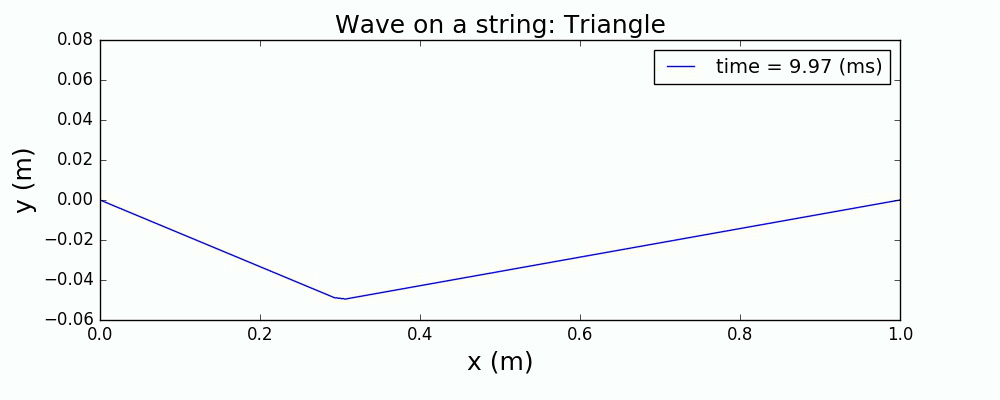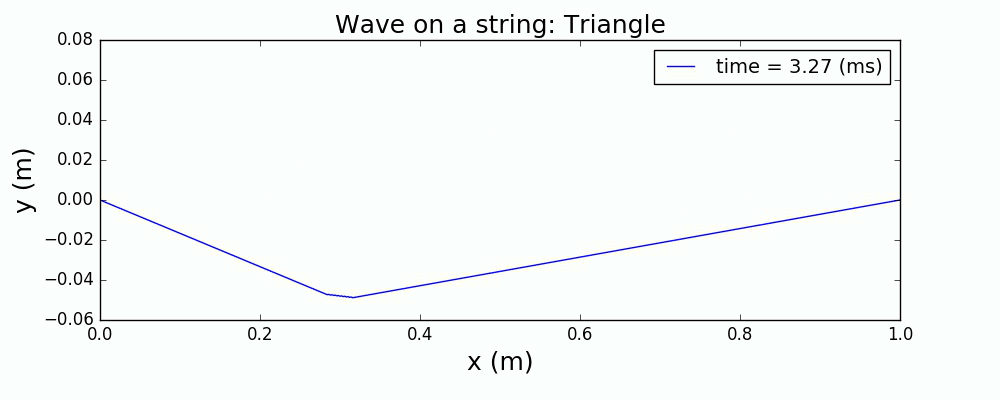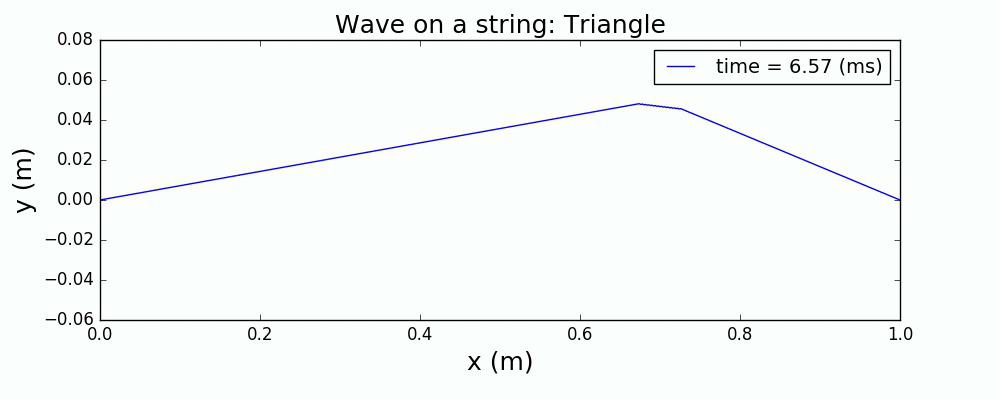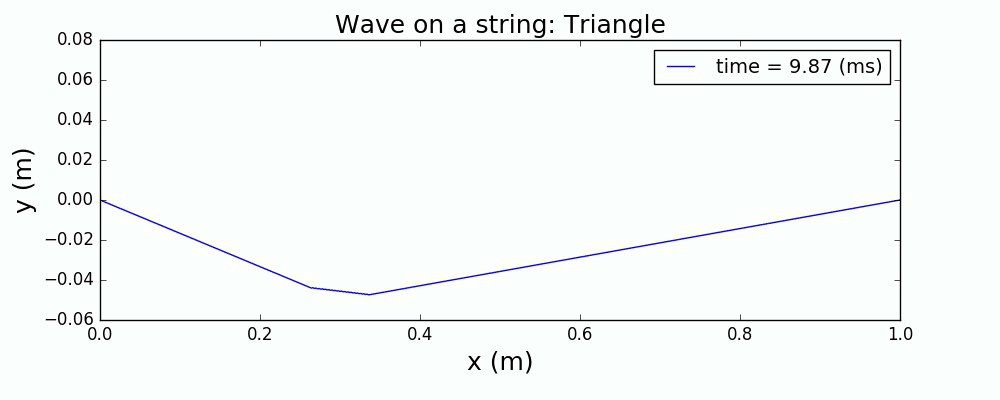
图5 将绳上一点拉起绳上给定点位移的功率谱
将绳上某点的振动信号作快速傅里叶分解并取模平方,得到信号的功率谱展示如下。在不同位置激发、在不同位置观察时,功率谱呈现不同特征,有的峰位可以缺失。
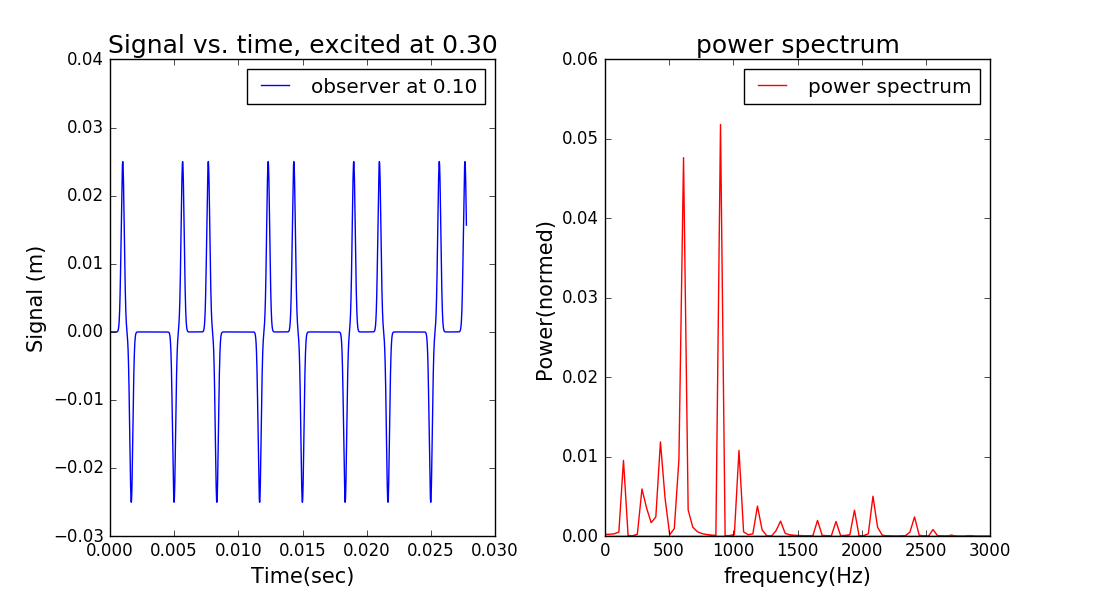
图6 在离端点10%位置观察绳波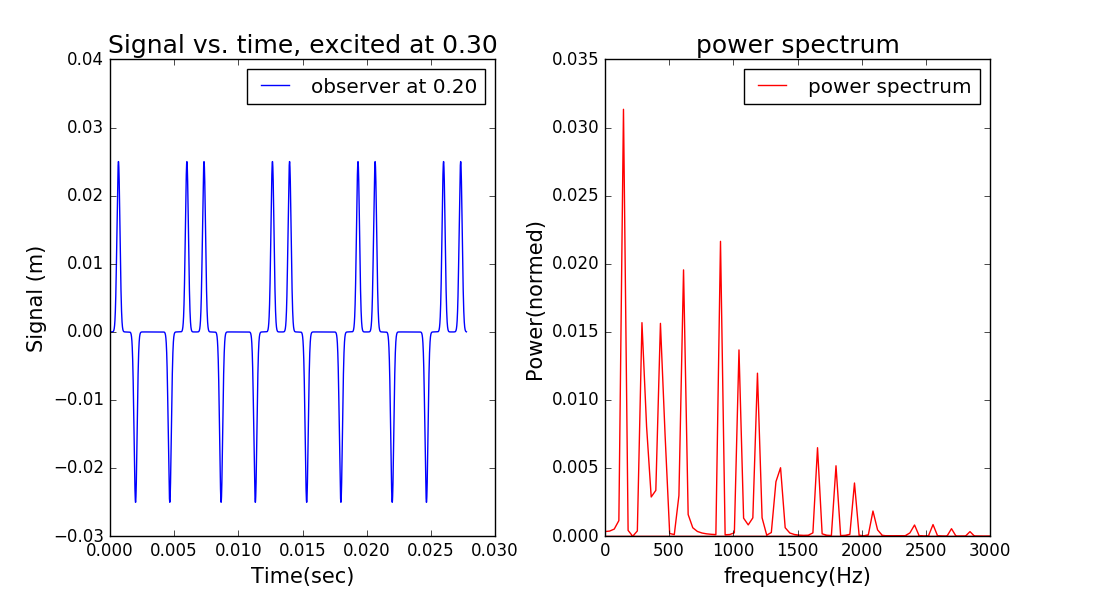
在离端点20%位置观察绳波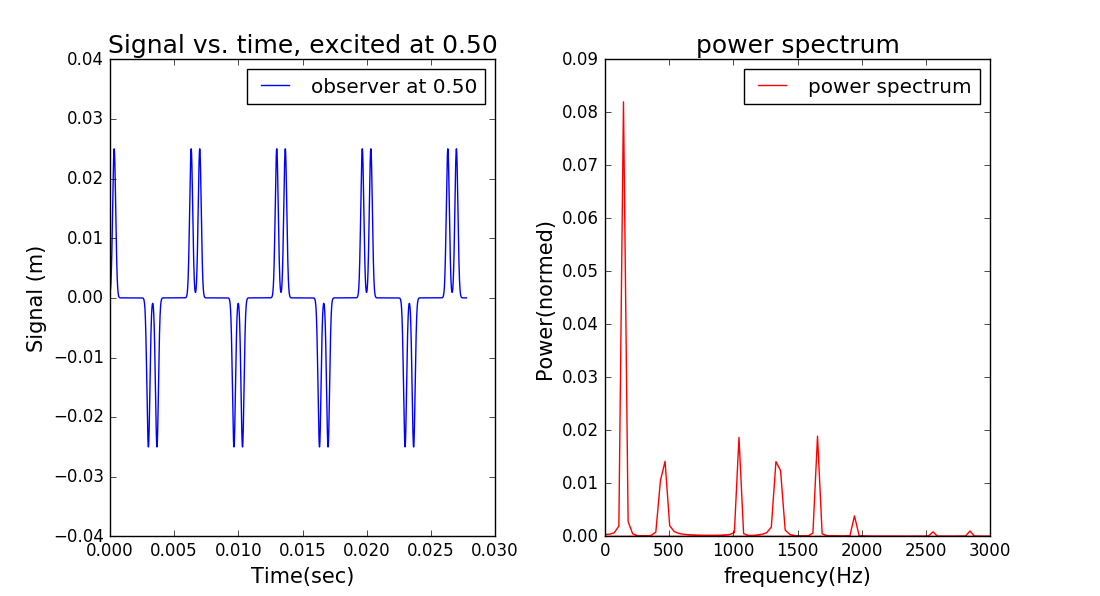
在离端点50%位置观察绳波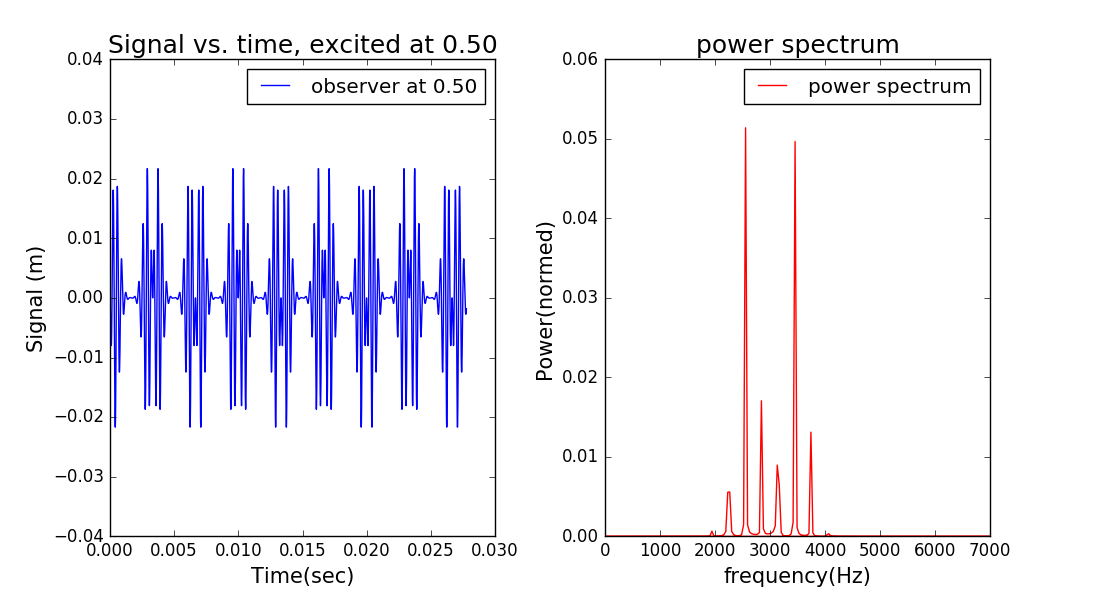
图9 高斯+正弦波包激发的频谱小结
本次作业展示绳波的运动过程。观察了不同激发形式的绳波随时间的演化过程。给出了在绳上给定点观察绳波信号的功率谱。
致谢和引用
[1] 计算物理;Nicholas J. Giordano, Hisao Nakanishi.
[2] 常用数学符号的LaTex表示方法;http://www.mohu.org/info/symbols/symbols.htm.
[3] matplotlib-绘制精美的图表;http://old.sebug.net/paper/books/scipydoc/matplotlib_intro.html.
