计算物理第6次作业 抛体运动

　　　　作者：陈洋遥 学号2013301020169 更新时间：20160403

内容目录

本文摘要

　　本次作业是为编写程序解决抛体运动问题。抛体运动是我们熟知的经典问题，在不计入空气阻力时，其运动方程十分简单，可以直接积分求解；但若引入空气阻力，则使抛体的运动方程变得十分复杂，一般只能数值的求解；特别是当计及空气阻力形式与海拔高度等复杂因素的关系时，抛体运动方程将更加复杂，我们将利用欧拉方法求解其运动方程。
　　另外，研究抛体运动对于炮弹轨迹、姿态问题具有重要意义。为使模型简化，我们暂不考虑炮弹的大小，只将其作为抛体质点处理，并利用此模型研究炮弹飞行射程对初速和发射角的依赖关系。我们利用数值方法计算靶位任意时欲命中靶所需的初速度或发射角，并估计命中靶位所需的最小初速度。相应的习题由课本Problem2.9和2.10给出。

研究背景

抛体的运动

　　抛体运动是牛顿运动方程处理力学问题的典范。在不计入空气阻力的情况下，抛体只受到重力，因而其运动规律由牛顿运动方程给出

$$\begin{equation} \left\{ \begin{aligned} \frac{\mathrm{d}^{2}x}{\mathrm{d}t^2}&=0 \\ \frac{\mathrm{d}^{2}y}{\mathrm{d}t^2}&=-g \\ \end{aligned} \right. \tag{1} \end{equation}$$
其中$g$是重力加速度。这是一个十分简单的方程，容易解析的求解。但倘若考虑其他的力(例如空气阻力等)，则还需在方程右边增补其他项，这将会使得实际抛体的运动情况更加复杂，很多情况下实际抛体的运动方程可以写为
$$\begin{equation} \left\{ \begin{aligned} \frac{\mathrm{d}^{2}x}{\mathrm{d}t^2}&=f_x(x,y,v_x,v_y;t) \\ \frac{\mathrm{d}^{2}y}{\mathrm{d}t^2}&=-g+f_y(x,y,v_x,v_y;t) \\ \end{aligned} \right. \tag{2} \end{equation}$$
其中$f_x(x,y,v_x,v_y;t)$，$f_y(x,y,v_x,v_y;t)$是单位质量抛体在$x$，$y$轴方向受力，其形式需根据实际情况确定。在许多情况下，仅考虑空气阻力对速度二次方的依赖项，再考虑空气是热的不良导体，建立大气绝热模型可以具体给出$f_x$，$f_y$的形式为
$$\begin{equation} \left\{ \begin{aligned} f_x&=-B(1-\frac{ay}{T_0})^{\alpha}vv_x/m \\ f_x&=-B(1-\frac{ay}{T_0})^{\alpha}vv_y/m\\ \end{aligned} \right. \tag{3} \end{equation}$$
其中$m$为抛体质量，$B$是不显著依赖于抛体性质和状态的常数，$\alpha$对空气约为$2.5$，$T$是热力学温度，而$a$是经验数，约是$6.5\times10^{-3}\mathrm{K/m}$。因此，方程组$(2)(3)$结合一定的初始条件就完全确定了抛体的运动状态$^\mathrm{[1]}$。

欧拉法求解抛体运动

　　上面的方程形式较为复杂，适宜用数值方法求解，我们这里使用课本上介绍的欧拉法来求解上面的方程。将二阶方程降阶，并将微分近似以差分代替，即得到近似描述抛体运动的四个代数方程

$$\begin{equation} \left\{ \begin{aligned} x_{i+1}&=v_{x,i}\Delta t+x_{i} \\ v_{x,i+1}&=f_x \Delta t+v_{x,i} \\ y_{i+1}&=v_{y,i}\Delta t+y_{i} \\ v_{y,i+1}&=(-g+f_x) \Delta t+v_{y,i} \\ \end{aligned} \right. \tag{4} \end{equation}$$
　　因此，只要知道前一时刻$t_i=i \Delta t$抛体的位置、速度，即可求得下一时刻$t_{i+1}=(i+1) \Delta t$时刻抛体的位置、速度；如此反复迭代，最终可以得到任意时刻抛体的运动情况。此即下面求解抛体运动的原理。
由于上面的方程是近似成立的，因而不可避免的要引入误差。不难证明欧拉法每一步的误差量级是$\Delta t^2$，而在给定总时间内的总体误差将是$\Delta t$量级，因此适当缩小步长$\Delta t$将有助于提高运算精度，但往往会使计算时间以$\frac{1}{\Delta t}$增加$^\mathrm{[2]}$，因此需要权衡两者利弊，取一在给定时间不产生显著误差的的步长即可，下面的计算将会体现这一点。

抛体运动的研究

有空气阻力的情形

• 运动方程的解
  　　空气阻力使得抛体(这里不妨取作炮弹)的运动情况变得复杂，但并不会为数值求解炮弹的抛体运动带来多大麻烦。我们利用欧拉法求解炮弹抛体运动的差分方程$(4)$即可得到炮弹运动的解，程序在github中给出(ch2_projectile_20160402.py)。我们取炮弹初速度为$v_0 =700.00 \mathrm{m/s}$，抛射角$\theta_0=45.0^{\circ}$时绘出其运动图像如下图1左图所示。
  
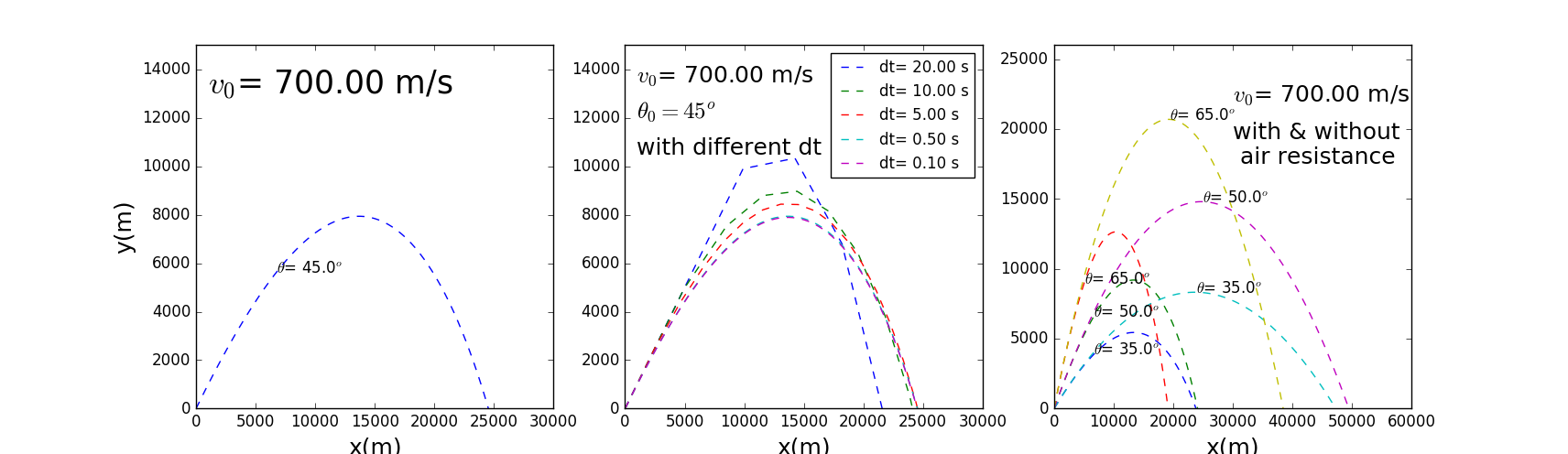
  　　　　　　　　　　　　　　　　　　　　图1 有空气阻力时的抛物运动
　　　　　　计算时，初速度取700m/s，发射角度取45°，来研究数值解对步长的依赖性，以及有、无空气阻力时解的差别　　
  　　

• 数值收敛性分析
  　　由于我们仅仅对方程进行数值求解，而数值步长$\Delta t$是决定解的好坏的决定性因素。如背景中所说，过长的步长将会使解显著偏离真实运动，而过长的步短则会使计算缓慢。我们逐步减小步长取值，直到解不显著依赖于步长选取为止，如上图1中图所示。我们取步长分别为$\Delta t =$ $20.00 \mathrm{s}$， $10.00 \mathrm{s}$， $5.00 \mathrm{s}$， $0.50 \mathrm{s}$， $0.10 \mathrm{s}$，可以发现随着步长减小，抛体运动轨迹形态逐渐发生变化，当步长取到$\Delta t =$ $0.50 \mathrm{s}$和$0.10 \mathrm{s}$时，两者轨迹不再有明显差别，因此可以断定

  • 数值解是收敛的，不会在步长较小时出现振荡的情况，因此可以相信解的准确性；
  • 当步长取到$\Delta t =$ $0.50 \mathrm{s}$时，再减小步长已经不能显著改善解的精确性，并且会延长计算时间。因此我们将选定$0.50 \mathrm{s}$作为我们的步长，在后面的计算中，也一律使用此步长进行计算。
• 与无空气阻力的差别　　
  　　直观上不难相信，空气阻力的存在会显著影响炮弹运动的性态。我们只需分别给出有、无空气阻力时的炮弹运动轨迹，即可看出两者的差别，如图1右图所示。我们分别作出两种情况下当抛射角取不同值时的轨迹，由图以及具体计算可以得到如下结论
  
  • 空气阻力将使炮弹的射程显著减小，减小量几乎是无空气阻力时的$1/2$，因此要提高炮弹的射程，一个有效的办法就是减少空气阻力，技术上可以通过适当设计炮弹形状而做到，或者采用燃料推进将炮弹送至高空以减少空气阻力；
  • 空气阻力还会影响炮弹轨迹的性态。具体来讲，数值地不难得到无空气阻力时炮弹最大射程(约$50250 \mathrm{m}$)是当抛射角为$\theta_0 = 45.0^{\circ}$时取到，而有空气阻力时可以计算炮弹最大射程(约$24550 \mathrm{m}$)则是当抛射角为$\theta_0 = 43.0^{\circ}$时取到,可见，空气阻力还会显著影响射程对抛射角的依赖关系，因此实际运用中应根据实际阻力条件确定发射角以保证炮弹能打得更远。

辅助精确打击系统 　　

• 问题的引入
  　　在实际过程中，炮队的目标往往不是固定于地面的死靶，其高度可能是任意的。另外，由于地形因素，炮队本身的高度也往往不确定，因此不能只考虑打击同高度地面目标的情况，而是希望对于相对于炮队任意高度、任意距离(在射程范围之内)的目标予以“精确打击”。为实现这一点，就需要程序通过给定炮队位置、靶位置来自动计算需要以多大速度、多大角度来投射炮弹以命中目标。由于炮弹出膛速度往往是确定的，因而我们下面先考虑以确定速度出膛的炮弹以何种抛射角出射时能命中目标；而有的炮弹抛射系统具有可变的出膛速度，这种情况下往往希望出膛速度尽量小以节省火药，因此就要确定炮弹命中目标所需最小出膛速度以及相应的抛射角，我们将在后面也讨论这个问题。 　　

• 恒定出射速度时的中靶问题
  　　下面就先考虑炮弹出膛速度恒定，而炮队位置和靶位任意给定时，以何种抛射角发射才能命中目标的问题。我们仍然利用欧拉法求解炮弹抛体运动的差分方程$(4)$得到炮弹运动的解，程序在github中给出(ch2_projectile_target_20160403.py)。我们还是取炮弹初速度为$v_0 =700.00 \mathrm{m/s}$时给定不同炮队位置和靶位的计算结果，如下图2所示。由具体计算和对图分析可以得到

  • 要命中目标，抛射角取值的可能范围其实是很大的。下图中中靶所需的抛射角下限可至$30^ {\circ}$左右而上限可达$70^{\circ}$左右。针对目标靶位任意的情况，就需要对抛射角进行扫描以确定合适的抛射角。然而不同的扫描方式可能会严重决定计算速度。 如果对$(0^{\circ},90^{\circ})$范围内均匀扫描，则及时扫描1000个角度，也只能保证达到千分之一(即约$30 \mathrm{m}$)左右的精度，这显然是不够的，因而，为提高扫描速度，程序中使用了类似“二分法”的扫描方法，每次粗扫之后，通过炮弹与靶位的最近距离来缩小扫描范围，再次扫描；以此类推，所需扫描的范围将以指数形式衰减，可以不必太大的计算量就得到很可观的精度(具体请参见程序内)。例如，本程序计算中取了扫描迭代次数为15次，就达到了很高的精度，炮弹与靶位的偏差约在$10 \mathrm{m}$左右，若要进一步提高精度，则只需要提高迭代次数或者提高python的计算精度即可。
  • 实际过程中，炮弹可能远不止受到空气阻力影响。但作为一个较理想的模型，本程序给出了基本的操作原理，下图2中，无论炮队发射位置和靶的位置如何，都可以通过调整发射角度以命中目标，这实际上为实际炮弹命中问题提供了基本思路。
    
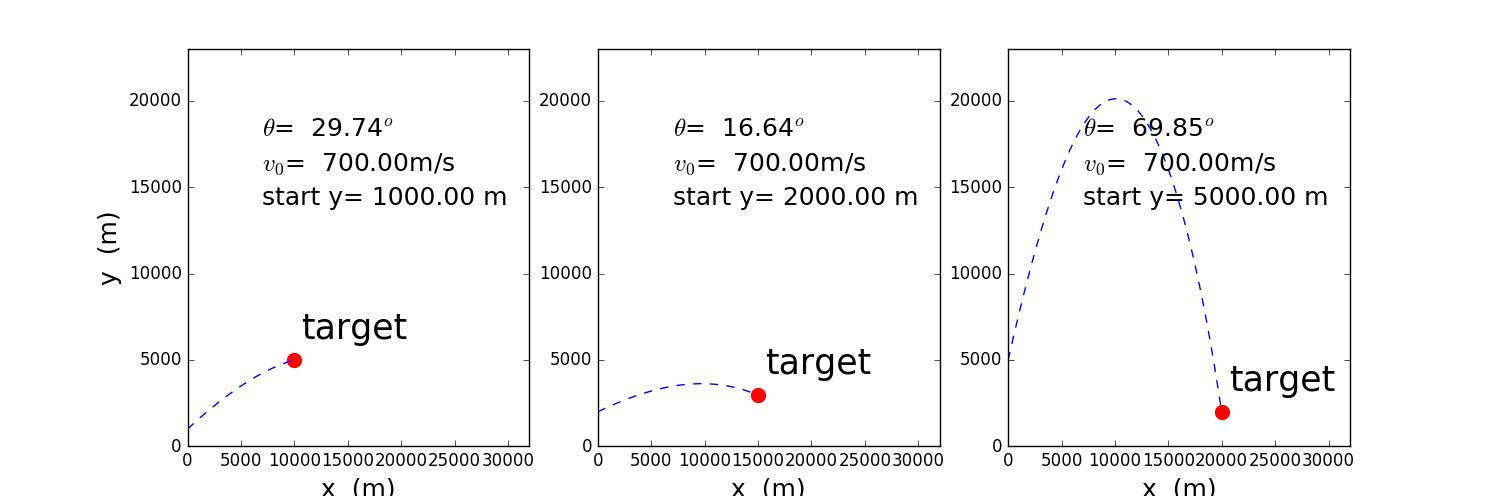
    　　　　　　　　　　　　　　　　　　　　图2 恒定出射速度时的中靶问题　　
　　　　　　计算时，初速度取700m/s，设置不同的靶位以及炮弹出射位置，来获取发射所需要的出射角度　　
    　　
    　　

• 出膛速度可变时最小发射速度问题
  　　若炮弹的出膛速度可以变化，则可以寻找一个最小的出膛速度来命中目标，这样可以节省火药。我们仍然利用欧拉法求解炮弹抛体运动的差分方程$(4)$得到炮弹运动的解，程序在github中给出(ch2_projectile_target_minvelocity.py)。这里，我们不仅要对炮弹的初速度进行扫描，还要对炮弹的发射角进行扫描，以求得命中靶位的最小所需发射速度及相应的发射角，如下图3所示
  　　　　
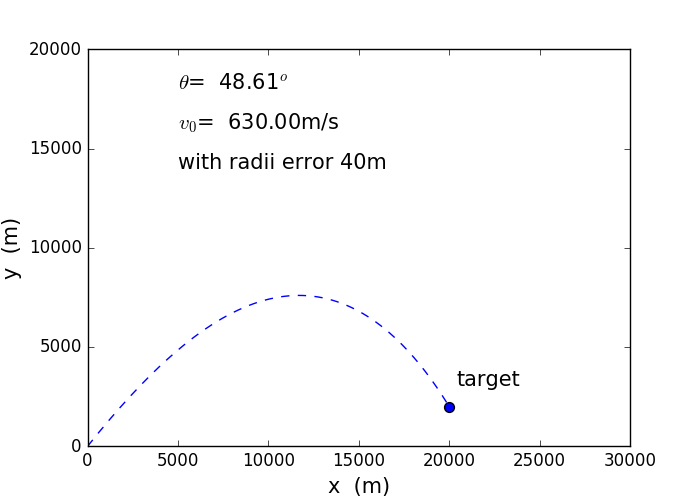
  　　　　　　　　　　　　　　　　　　　　图2 出膛速度可变时最小发射速度问题
　　　　　　计算时，初速度和发射角均不确定，通过类似“二分法”的方法，逐次缩小扫描范围，来获得发射所需初速度和抛射角
  可以看到，对于任意靶位，当炮弹出射速度可以变化时，仍然可以扫描各种发射情况(初速度、发射角)来命中目标所需最小发射速度及相应的发射角，这里，因为要对发射的两个参数同时扫描，因而命中的圆周误差上限是$40 \mathrm{m}$，要提高精度只需增加扫描迭代次数和计算精度即可。

小结

　　本次作业讨论了空气阻力存在时炮弹飞行轨迹问题，讨论了欧拉法解炮弹轨迹问题的数值解收敛性问题，分析了有、无空气阻力时炮弹轨迹差异，并将此方法联系到实际的辅助精确打击系统，分别给出了炮弹出膛速度确定时发射角问题，炮弹出膛速度不定时最小抛射速度问题。本程序的方法和结果将对炮弹发射问题具有一定的借鉴意义。

致谢和引用

[1] 计算物理；Nicholas J. Giordano, Hisao Nakanishi
[2] 数值分析；李庆阳，王能超
[3] 常用数学符号的LaTex表示方法，http://www.mohu.org/info/symbols/symbols.htm
[4] matplotlib-绘制精美的图表，http://old.sebug.net/paper/books/scipydoc/matplotlib_intro.html