计算物理第12次作业　Resonances: Kirkwood Gaps

作者：陈洋遥 学号2013301020169 更新时间：201605015

内容目录

本文摘要

　　在太阳系中，最早发现的几颗行星到太阳的距离可以由Titus-Bode序列给出。然而，在火星和木星之间，却有一个空缺。经过细致的观察，天文学家自1800年左右逐渐在该位置发现了许多的小行星，形成了庞大的小行星带。实际上，小行星在整个太阳系内均有分布，将小行星密度按与太阳的距离绘制成曲线，可以发现在许多位置几乎不能出现小行星。在19世纪中期，天文学家Daniel Kirkwood即发现了小新星的这种空缺现象，后来，这些小行星不能分布的位置被称为KirkWood gaps。本次作业完成课后习题4.18，讨论Kirkwood gap附近小行星的运动与gap的宽度。
　

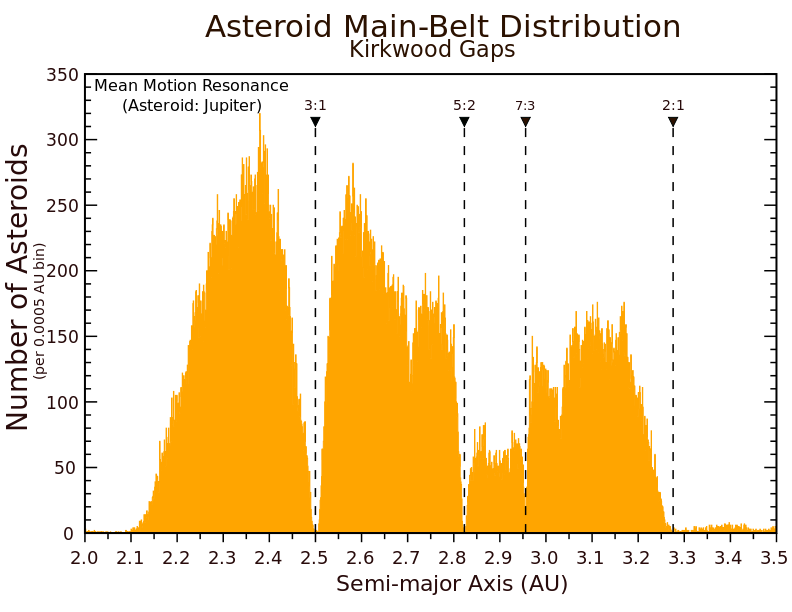
图1 小行星密度分布(图片来自维基百科) 在小行星周期与木星周期成整数比的位置，小行星几乎不能存在

研究背景

　　KirkWood gap的形成原因$^{[1]}$可以用木星与小行星的共振来解释。木星是太阳系中最大的行星，其引力对小行星运动会产生不小的影响。当木星的轨道周期与小行星的轨道周期成整数比时，小行星最靠近木星的位置将是确定的，在这些位置上，小行星受到木星引力的摄动非常明显，这些摄动长期累积，导致小行星的轨道成为不断进动的椭圆，且离心率越来越大，最终有可能撞上其他的行星，这样的现象与常见的共振现象有异曲同工之处，可以认为是太阳系中的共振现象。而小行星周期与木星周期不成整数比时，近木点位置则是不确定的，因此木星的摄动在长时间内相互抵消，不能对小行星的轨迹产生明显的影响。下面就在Kirkwood gaps附近利用数值方法模拟小行星的运动。
　　小行星和木星均除受到太阳引力外，他们之间还存在引力相互作用。考虑到太阳的质量比较大，因此不考虑太阳的运动。这样，小行星和木星的受力如下

$$\begin{equation} \left\{ \begin{aligned} \textbf{f}_{a} &= -\frac{GM_s M_a}{r_{a,s}^3}\textbf{r}_{a,s}-\frac{GM_j M_a}{r_{a,j}^3}\textbf{r}_{a,j} \\ \textbf{f}_{j} &= -\frac{GM_s M_j}{r_{j,s}^3}\textbf{r}_{j,s}-\frac{GM_j M_a}{r_{j,a}^3}\textbf{r}_{j,a} \\ \end{aligned} \right. \tag{1} \end{equation}$$ 　　
利用牛顿第二定律$\textbf{f}=m\textbf{a}$，即可得到两者的动力学方程。将动力学方程向两个坐标轴投影，并改写成差分方程，即可利用Euler-Cromer方法数值求解小行星和木星的运动。考虑到小行星质量远比木星小，因此大可不必考虑小行星引力对木星的影响。下面就来展示木星引力对小行星运动的影响。

Kirkwood gaps附近小行星的运动

1/2周期的gap附近小行星的运动

　　可以预见，当小行星与木星的周期比$T_a/T_j=1/2$时(即在1/2 Kirkwood gap附近)，小行星在近木点所受引力影响经长期的、单向的积累，最终将导致小行星的运动严重偏离圆轨道运动。利用数值方法，在此gap处，即$r_0=0.2758AU$及其附近作出$200yr$内小行星运动轨迹如下图(1)所示，相应的程序见ch4_Kirkwood_trajectory.py。可见，当小行星处于gap中心时，其受木星影响十分强烈，而在gap附近，例如$r_0=0.3800$处，尽管小行星离木星较近，但是由于偏离了共振峰，因此摄动较小。1/2 gap处由于小行星运动与木星运动周期匹配的特别好，因而受木星影响特别大，从后面的图3可以看出，共振峰的高度可以到达0.3左右。

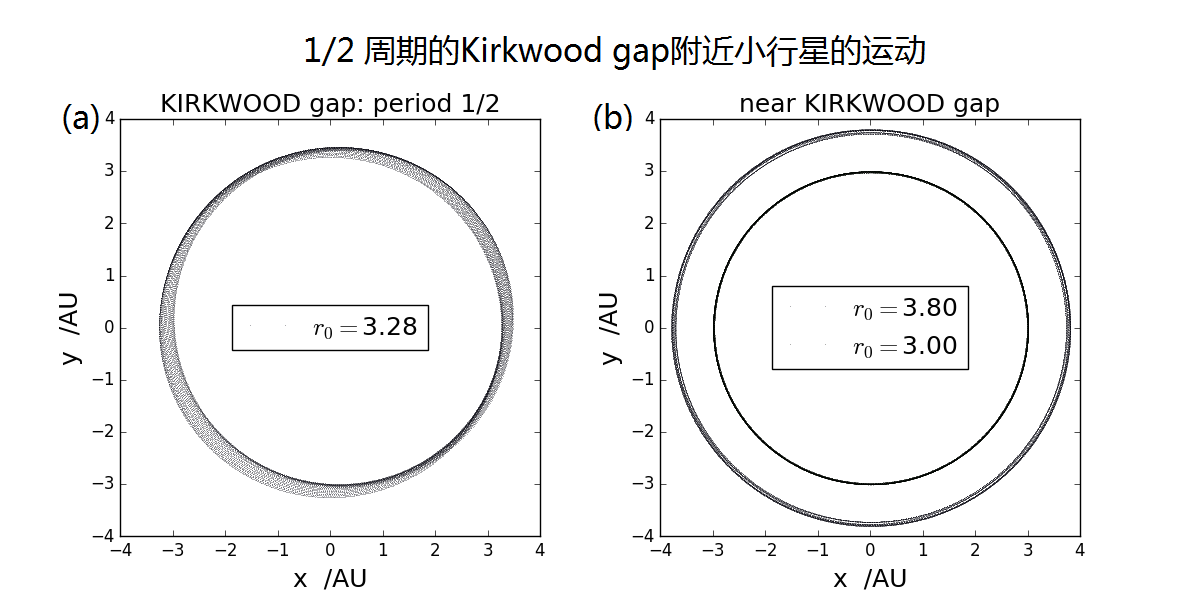
图2 1/2周期的Kirkwood gap附近小行星的运动 不考虑小行星引力对木星运动的影响，作出的小行星运动在$200yr$内的轨迹。当小型新周期接近木星周期的一半，即其初始运动半径$r_0=3.28 AU$时，小行星运动收木星影响强烈，其轨迹类似进动的椭圆。图(b)所示，当小行星运动周期偏离木星周期的一半时，小行星的运动受木星影响较小。

　　为了给出共振峰的宽度，看看在多大的范围内小行星运动会受到木星引力的显著影响，我们作出小行星运动的振幅-半径共振曲线如图2所示。在每一个初始半径$r_0$处，在$200yr$的时间内，其受木星影响的强度由$200yr$内其离太阳距离的最大值和最小值的差与其初始半径的比$\delta r /r=(r_{max}-r_{min})/r$来刻画，图2所示是$\delta r/r_0-r_0$关系，可以发现，共振峰的实际位置并不是处在理论猜测的1/2周期轨道(即$r_0=3.2758AU$)处，而是略大一点，其原因可以分析如下：尽管在1/2周期的位置，小行星运动的周期与木星运动周期匹配的较好，但是当$r_0$增加时，小行星近木点离木星距离更近，因而每次摄动更强，综合考虑这两方面的因素，才能得到实际的共振峰位置。

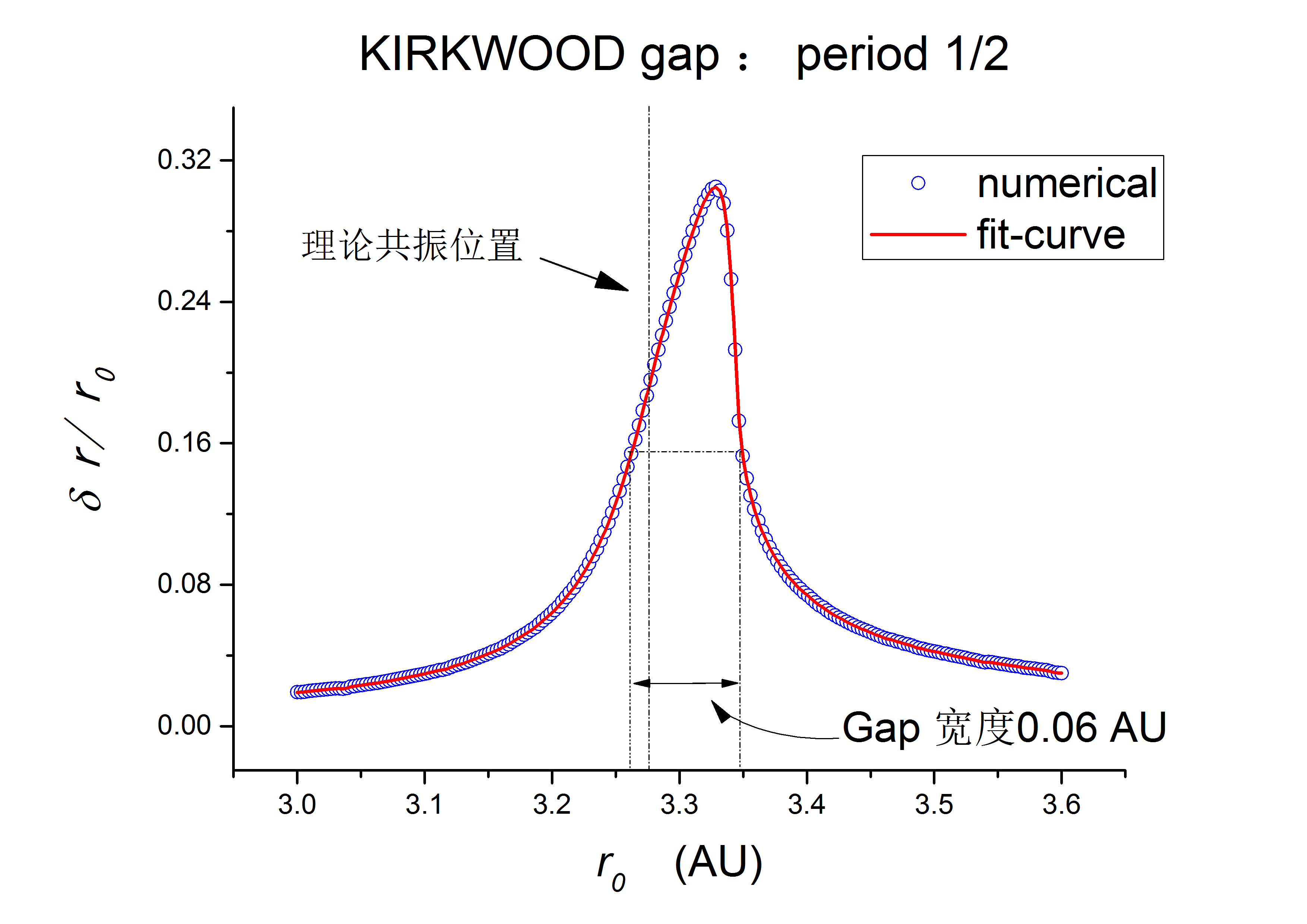
图3 1/2周期的Kirkwood gap的宽度不考虑小行星引力对木星运动的影响，作出小行星在1/2 Kirkwood gap附近的共振曲线。改变小行星离太阳的距离，其受木星影响的强度由$200yr$内其离太阳距离的最大值和最小值的差与其初始半径的比$\delta r /r=(r_{max}-r_{min})/r$来刻画， 理论上，小行星周期严格等于木星周期的一半，即其初始半径$r_0=3.2758AU$时，应该与木星发生共振导致其偏离最大，然而实际的共振距离却比估计上稍大一点。

其他Kirkwood gaps附近小行星的运动

　　从上面的分析可以看到，只要小行星运动周期和木星运动周期匹配得较好，就可以发生共振，而当小行星离木星更近时，受木星影响更为强烈。因此可以预见到，在距离木星更近的Kirkwood gaps处，小行星受木星影响应该更为强烈。下图4展示了$200yr$内，在比1/2 gap更近的两个gap，3/4 gap(也即$r_0=4.2925$)处和6/7 gap(也即$r_0=4.6922$)处的小行星运动情况，可以发现，当小行星位于6/7 gap处时，其近木点将离木星非常近，受木星影响非常强烈，再加上轨道周期匹配，其轨道严重偏离圆轨道运动。而在3/4 gap处，因小行星近木点离木星稍远一些，因而轨道偏离圆轨道程度并不大。

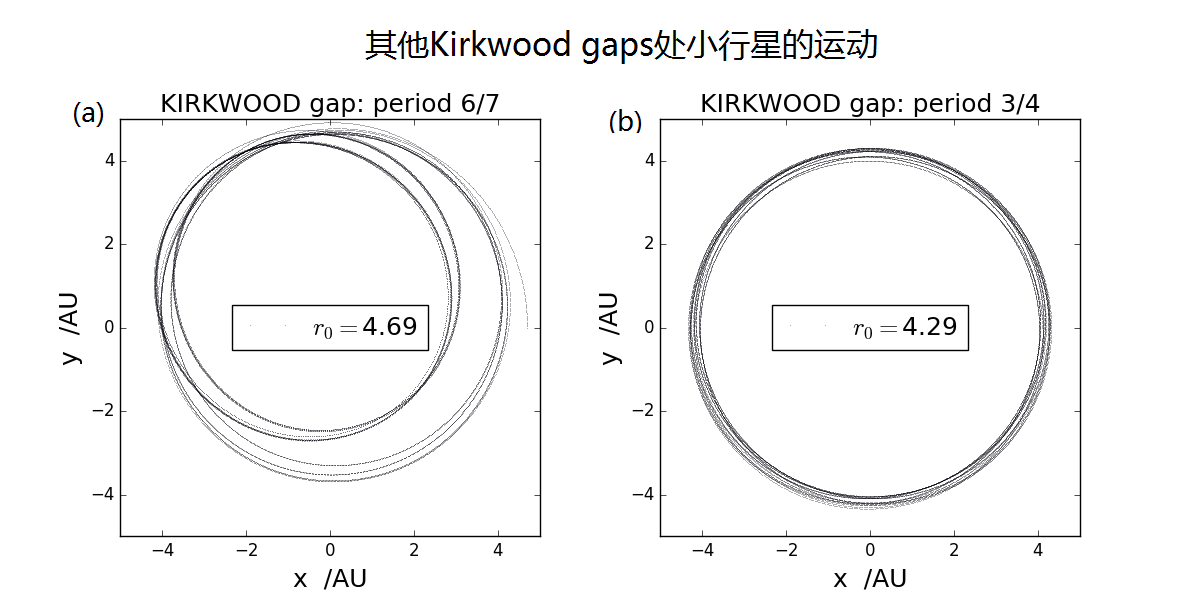
图4 6/7和3/4周期的Kirkwood gaps初小行星的运动 考虑其他Kirkwood gaps处小行星运动情况，图为在$200 yr$内小行星的轨迹。图(a)所示，在6/7周期的gap处，由于小行星近木点离木星非常近，小行星受强大的引力摄动，因而偏离圆轨道程度非常大，图(b)所示，在3/4周期的gap处，偏离则小得多

　　用同样的方法可以分析其他gaps处小行星运动情况。值得注意的是，当作出其他gaps处的振幅-距离共振曲线时，在2/5周期的gap处并没有发现共振峰，而是发现了一个共振谷，如图5所示。即在2/5 gap，$r_0=2.9230AU$附近，出现了特别稳定的情况。这个位置的共振谷宽度不是特别宽，只有$0.009AU$，深度在$0.001$0.001以下。因而不是十分明显。该谷的谷底的实际位置也和上面的共振峰一样，比严格的2/5周期对应的半径略大一点。另一个值得注意的地方是共振谷附近的精细结构，即在大的共振谷附近由小的共振谷，这些谷的出现应该是次级共振，即小行星与木星周期比$T_a/T_j$是两个较大的整数比导致的。

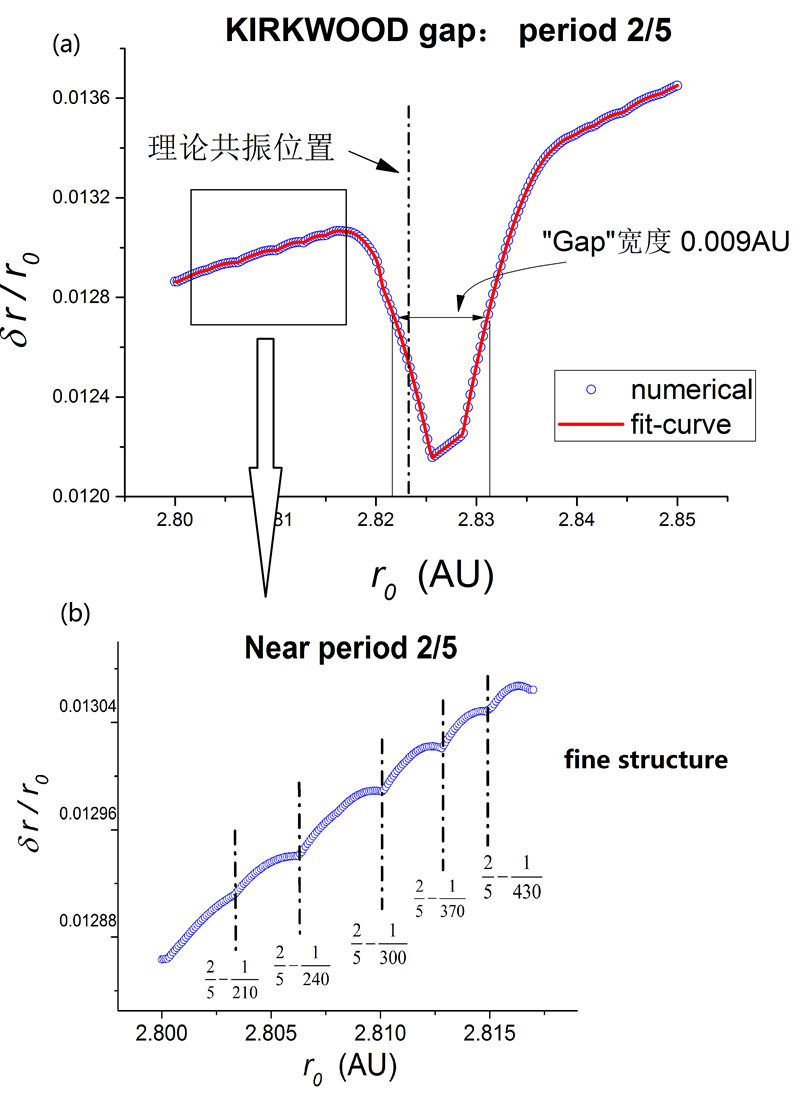
图5 2/5周期的Kirkwood gap处的反常情况当小行星运动周期与木星运动周期比为2/5时，理论上应发生共振使小行星运动严重偏离圆轨道，然而2/5周期的gap，即初始半径$r_0=2.9230AU$处，却发生了反常现象，由图(a)的$\delta r/r_0-r$曲线可见，在理论gap附近不是共振峰，而是一个共振谷，即在此位置附近小行星运动特别稳定。图(b)所示为共振谷附近的精细结构，即在大的共振谷附近由小的共振谷，这些谷的出现应该是次级共振，即小行星与木星周期比$T_a/T_j$是两个较大的整数比导致的。

小结

　　本次作业讨论了太阳系中小行星运动受木星引力影响的问题。在小行星周期与木星周期成整数比的轨道(即Kirkwood gaps)附近，小行星与木星发生共振，受木星引力影响单向累加使得小行星的运动显著偏离圆轨道运动。本次作业展示了这一现象，并具体求出了共振峰的位置和宽度，另外展示了某些共振位置的反常现象和精细结构。

致谢和引用

[1] 计算物理；Nicholas J. Giordano, Hisao Nakanishi.
[2] 常用数学符号的LaTex表示方法；http://www.mohu.org/info/symbols/symbols.htm.
[3] matplotlib-绘制精美的图表；http://old.sebug.net/paper/books/scipydoc/matplotlib_intro.html.