计算物理第13次作业　Potentials and Fields

作者：陈洋遥 学号2013301020169 更新时间：201605023

内容目录

本文摘要

　　静电势问题是经典电动力学的重要问题。在无源区域，静电势满足Laplace方程，从而只要在一定的边界条件下求解Laplace方程就可以得到静电势的空间分布。求解偏微分方程没有一般的方法，但是对诸如Poisson方程在内的一大类方程，可以采用所谓的松弛算法(relaxation method)去求解。本次作业完成课后习题5.7，讨论了松弛算法的三种具体情形(Jacobi、Gauss-Seidel、simultaneous over-relaxation(SOR))的迭代收敛速度问题。　 　

研究背景

　　无源区域的静电势问题的解可由麦克斯韦方程给出，这种情况下，静电势分布满足Laplace方程

$$\begin{equation} \nabla^2V=0 \tag{1} \end{equation}$$
在直角坐标系下将上述方程离散化就可以得到数值求解的方法。参照课本Chapter5开篇的方法，可以将静电势方程离散化为下述形式
$V(i,j,k)=\frac{1}{6} [V(i+1,j,k)+V(i-1,j,k)+V(i,j+1,k)+V(i,j-1,k)$
$$\begin{equation} +V(i,j,k+1)+V(i,j,k-1)] \tag{2} \end{equation}$$
可见，只要合理的给出空间的静电势，使之满足上述要求，则就得到Laplace方程的解。然而要直接猜出符合上述方程的解并不容易，一个可行的办法是先随便猜一个解，再把猜的解带入上述方程右边，得到一个新的解。如此不停的将解更新，直到收敛为止。这就是所谓的松弛算法。实践表明，上述过程对初值的选取不明显依赖，并且经过一定的迭代总是可以收敛到稳定值。然而迭代的方法不同会使得收敛速度大有区别，根据迭代方法的不同，松弛算法有不同的表现，这里研究教材上介绍的三种方法，即Jacobi算法、Gauss-Seidel算法，SOR算法的收敛速度问题。他们的区别仅仅在于：Jacobi算法对整个空间点都用旧值计算新值，而Gauss-Seidel算法则用更新后的值计算新值，SOR算法则将欲更新值与老值的增量乘以一定的倍数后加到老值上作为新值以使迭代收敛更快。下面就来具体讨论三种算法的收敛速度问题。

静电势问题的求解

静电势问题的求解——平行板电容附近的电场

　　平行板问题是一个十分经典的问题，对其进行数值求解可以检验算法的稳定性等问题。为简单起见仅讨论二维问题，或者说认为平行板系统沿着某一方向是对称的。取两块平行板的电位分别为$+1V,-1V$，或者其他值，取正方形边界的电势为0，计算体系电势分布如图1所示，相应的程序可见ch5_electric_capacitor.py。所得到的结果符合我们队平行板电容器电场的认识。

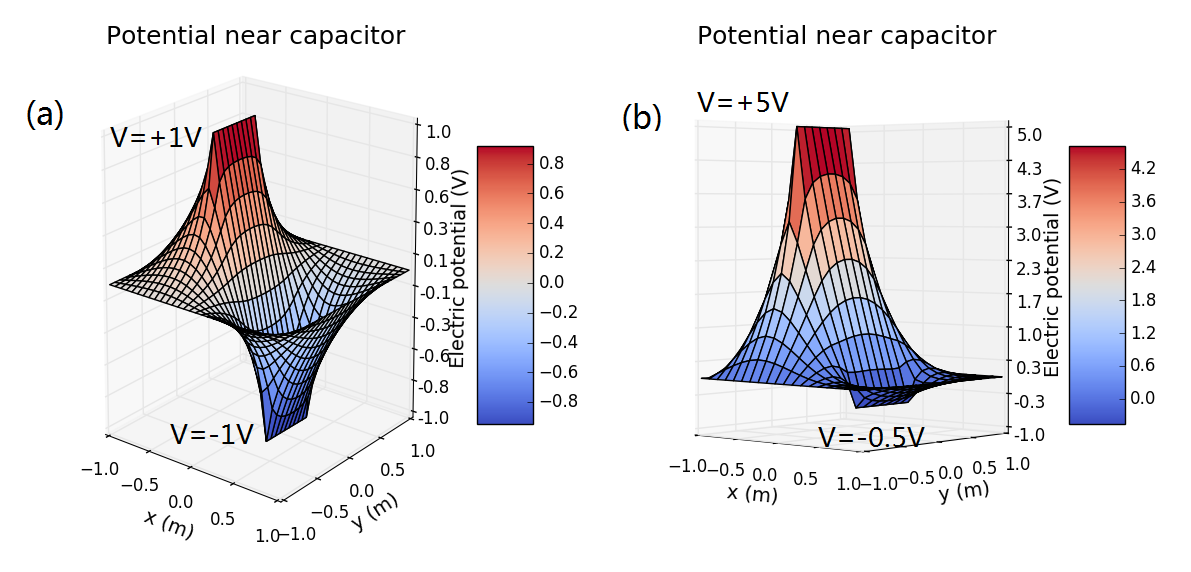
图1 平行板电容的电电势分别 　　图1展示平行板电容的电位分布，这里取两板的电位分别为$+1V,-1V$，边界取为正方形边界，边界电位为0。

　　要表示电场的空间分布，另外的方法是利用准三维的方法：用等势面(线)去表示电势，用电场线去表示电场分布。下面的图2展示这两种表示方法，相应的程序可见ch5_electric_field.py。 可以发现平行板的电场具有一定的对称性。图(a)展示等势面，图(b)展示电场线，平行板电容在两板之间相当大区域内确实有十分均匀的电场，平行板外的电场则小一些。这些都符合平行板电容的电场特征。

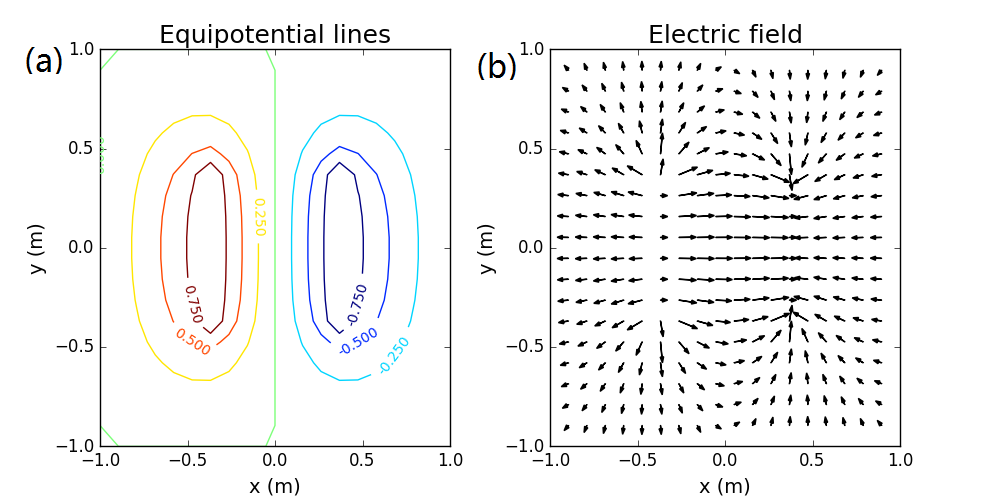
图2 平行板电容器的等势面(线)和电场分布　　图2展示平行板电容器之间和外部区域等势面(线)和电场分布，为简单起见这里认为电场沿$z$方向不变。可以发现平行板的电场具有一定的对称性。图(a)展示等势面，图(b)展示电场线，平行板电容在两板之间相当大区域内确实有十分均匀的电场，平行板外的电场则小一些。

不同迭代方法的收敛快慢

　　上面已经提及，不同的迭代方案的收敛速度有较大差异，特别是对于较大的系统，利用收敛较快的方法解决偏微分方程问题将节省大量的计算时间。这里展示松弛算法的三个实例——Jacobi、Gauss-Seidel和SOR算法的计算收敛速度。在同样的问题下(平行板电容问题)，对相同的收敛判据，三种方法收敛所需迭代次数展示如图3所示。相应的程序见ch5_electric_capacitor_runtime.py。从图3(a)中可以看出，SOR方法所需迭代次数最少，且随着计算区域尺度$L$的增加仅仅是线性增大的，另两种方式则是二次方增加的。相应的耗时也展示如下图(b)所示。

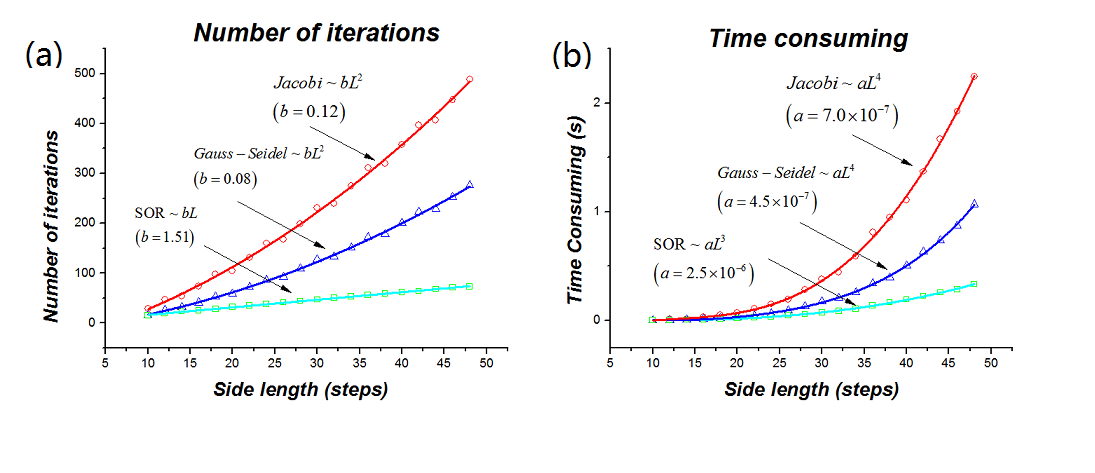
图3 不同方法的迭代次数和耗时差异　　图3展示不同数值方法在一定精度要求下迭代次数和耗时的差异。图(a)给出Jacobi、Gauss-Seidel以及SOR方法的迭代次数，而图(b)给出了他们的计算耗时。可以发现，SOR方法的迭代次数随计算区域尺度$L$呈线性变化，而Jacobi、Gauss-Seidel方法的迭代次数则随计算区域的尺度$L$呈二次方变化，只不过前者的系数比后者的要大一些。而三者的计算耗时的变化规律则基本相当于计算迭代次数$\times L^2$。计算中取两极板电位分别为$-1V,+1V$。迭代到每个计算点平均变化满足$\delta V<(V_{+}-V_{-})\times 10^{-5}$为止

　　从上面的讨论可以看出，一般来讲SOR算法收敛的比较快，然而SOR算法中尚有一个参数$\alpha$(见课本P142)可以调控。适当选取这个参数有利于使体系收敛得更快。下图4展示了一定计算条件下收敛所需迭代次数随$\alpha$的变化规律，相应的程序可见ch5_electric__SOR.py。下面曲线的特征是当$\alpha$趋近于0和趋近于2时都是发散的，并且在0和2之间有唯一最小值。因此，若能根据不同体系的具体情况，适当选取$\alpha$的值，对提高计算速度是十分有利的。

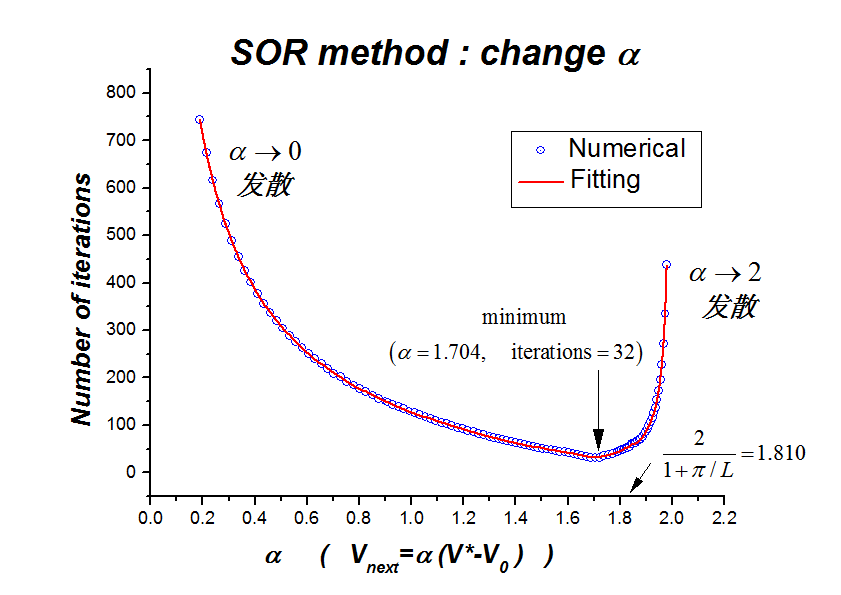
图4 SOR method 改变参数alpha 　　如图所示，SOR方法是将Gauss-Seidel方法中每次更新电位时的增量增加为原来的$\alpha$倍，选择合适的$\alpha$可以使电位收敛更快。这里展示了不同$\alpha$时的迭代次数，可见$\alpha$变化时确实有单一最小值，确实在$\alpha=\frac{2}{1+\pi/L}$附近。计算中的边长为$L=30$步，两块电容板电势分别为$V_{+}=-1V,V_{-}=+1V$，迭代到每个计算点平均变化满足$\delta V<(V_{+}-V_{-})\times 10^{-5}$为止。

小结

　　本次作业针对平行板电容的静电势求解问题。具体讨论了松弛算法的三种具体情形(Jacobi、Gauss-Seidel、simultaneous over-relaxation(SOR))的迭代收敛速度问题。
　　
　　

致谢和引用

[1] 计算物理；Nicholas J. Giordano, Hisao Nakanishi.
[2] 常用数学符号的LaTex表示方法；http://www.mohu.org/info/symbols/symbols.htm.
[3] matplotlib-绘制精美的图表；http://old.sebug.net/paper/books/scipydoc/matplotlib_intro.html.