计算物理第10次作业　LORENZ MDDEL AND BILLIARD

作者：陈洋遥 学号2013301020169 更新时间：20160502

内容目录

本文摘要

　　本次作业研究其他的混沌现象。LORENZ模型是E.N.LORENZ从气象问题中抽象出来的一个极简化的模型，但仍然能够有效展示混沌现象的产生，并且可以期待一般流体中也会拥有这样的混沌产生机制。另一个著名的模型是桌球模型。考虑桌球在无摩擦的台面上运动，当其碰壁时，则发生弹性碰撞而被反射。当台面形状高度对称时，单个桌球的运动是十分规则的，然而当台面形状略有不规则时，就容易出现混沌现象。下面就来展示这两个模型。本次报告展示作业3.26和3.31。

研究背景

　　Lorenz模型是从流体力学的Navier-Stokes方程在Rayleigh-Benard问题里简化得到的一个方程组，其反映了速度、温度、密度变量随时间演化的规律

$$\begin{equation} \left\{ \begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}&=\sigma(y-x)\\ \frac{\mathrm{d}y}{\mathrm{d}t}&=-xz+rx-y \\ \frac{\mathrm{d}z}{\mathrm{d}t}&=xy-bz \\ \end{aligned} \right. \tag{1} \end{equation}$$
其中$x,y,z$即使流体温度、密度、速度，而$r$反映由温差带来的驱动效果，$b$则反应流体阻尼。由于上式对实际问题太过简化，故不能期待其能预言正确的物理现象。我们要做的是展示这样简化的模型也能产生混沌现象。这样的方程一般来讲将给出振动解，因而欧拉法可能不适用。然而经过详细讨论$^{[1]}$可以发现欧拉法在数值求解此问题时仍然给出不错精度的结果。因此下面就采用欧拉法来求解此问题。
　　桌球模型则是另外一个常见的模型。即使桌球在台面上反射时是弹性的，且与台面之间没有摩擦，但只要台面形状对称性略低，则立即可以看到混沌现象。当台面上的桌球数目逐渐变多，并且球与球之间可以发生弹性碰撞时，问题则更加复杂，此所谓分子刚球(2d情况下是硬盘)模型，我们也将展示这样的结果。

LORENZ 模型

流体运动随时间的演化

　　LORENZ模型内流体运动显著依赖于驱动$r$，当改变驱动$r$的大小时，即可观察到混沌的产生和消失。下图1表明，当驱动幅度较小时，不产生混沌，而驱动幅度大一些时，则产生混沌现象，程序可见ch3_lorenz_phase.py。

图1 改变驱动强弱时，z vs time曲线取$\sigma=10,b=8/3$时Lorenz模型描述的流体运动，改变驱动$r$的幅度。(a)(b)所示当驱动幅度较小时，不产生混沌，流体在经过一段暂态过程后进入稳恒对流运动阶段。(c)图所示为$r=29.00$的强驱动情况，此时流体发生了复杂的混沌运动

相空间的图形

　　和前面的摆动问题一样，我们可以作出相空间$x,y,z$的图形，这样更能揭示混沌现象的内在规律性。另外，还可以作出相空间的截面，可以发现这样的截面是与初值无关的$^{[1]}$。也就是说，尽管混沌现象内禀复杂，其对初值极其敏感，但其相空间截面却与初值无关，是混沌运动的"不变量"，因而尽管不能预言混沌系统随时间演化规律，但其相图在一定程度上是可以预测的。程序和前面的是同一个程序。

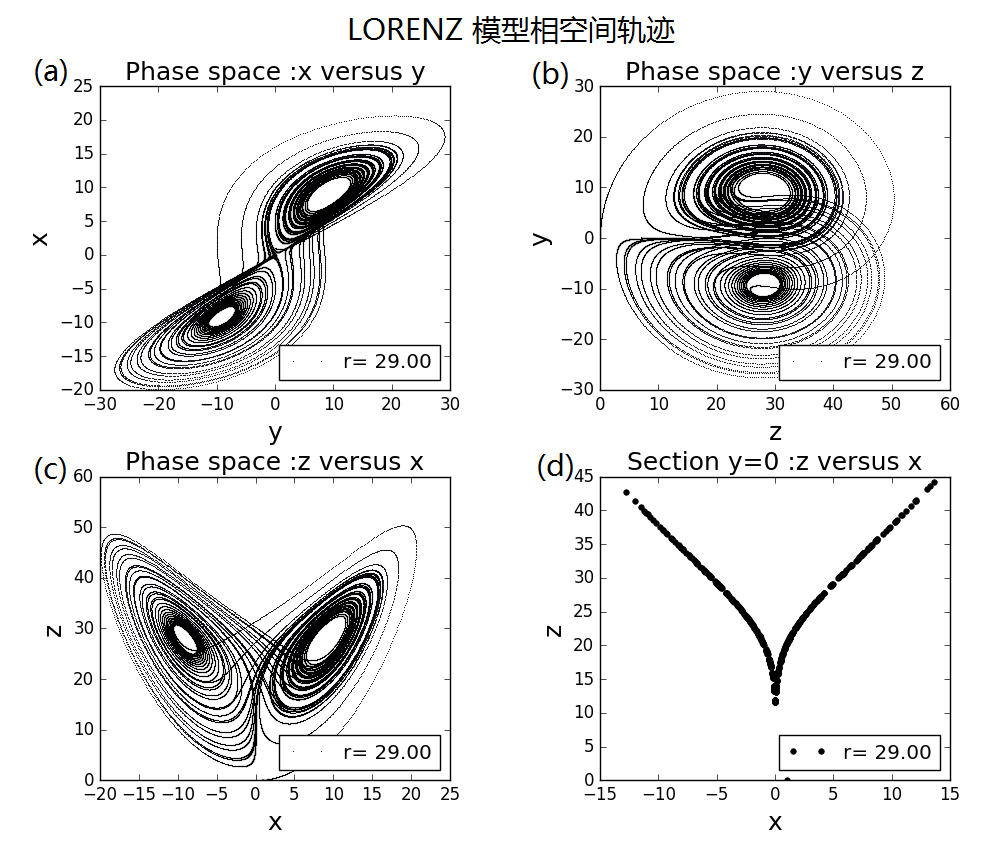
图2 不同方向观察混沌运动的相图取$\sigma=10,b=8/3$时Lorenz模型描述的流体运动，图(a)(b)(c)分别从三个不同方向观察混沌的相空间，而(d)则是取的相空间$y=0$的截面

　　同样可以直接在三维空间作出动态的相图。由于本人电脑一直不能用vpython，故用MMA作出动态图形，程序一并附在文末。结果如下图3所示

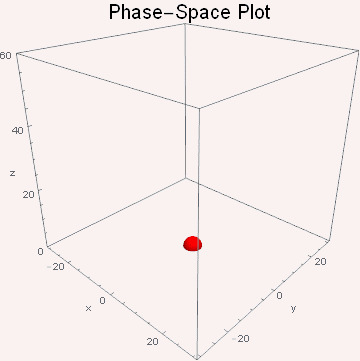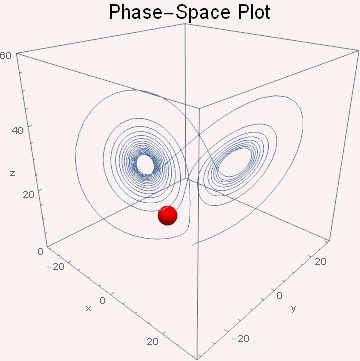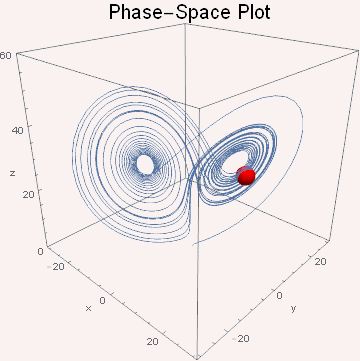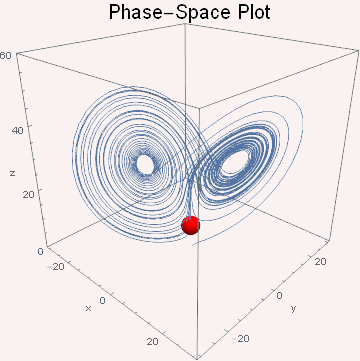
图3 三维空间的相图取$\sigma=10,b=8/3$时Lorenz模型描述的流体运动的三维相图，相随时间的演化竟然是不停地绕圈圈，还能交叉。

台球的运动

边界为运动场形时的台球运动

　　下面来展示台球运动。先考虑边界形状为半径为$r$的圆形，可以预见台球的运动应该是高度规则的。然后考虑所谓的体育场模型，即在两个半圆之间加上一块矩形区域，矩形长度为$\sigma r$，这样使得球台的对称性很大破坏。相应程序见ch3_billiard_trajectory.py，可以发现，现在台球的轨迹几乎可以铺满整个台面，运动无规律性也大大提高。

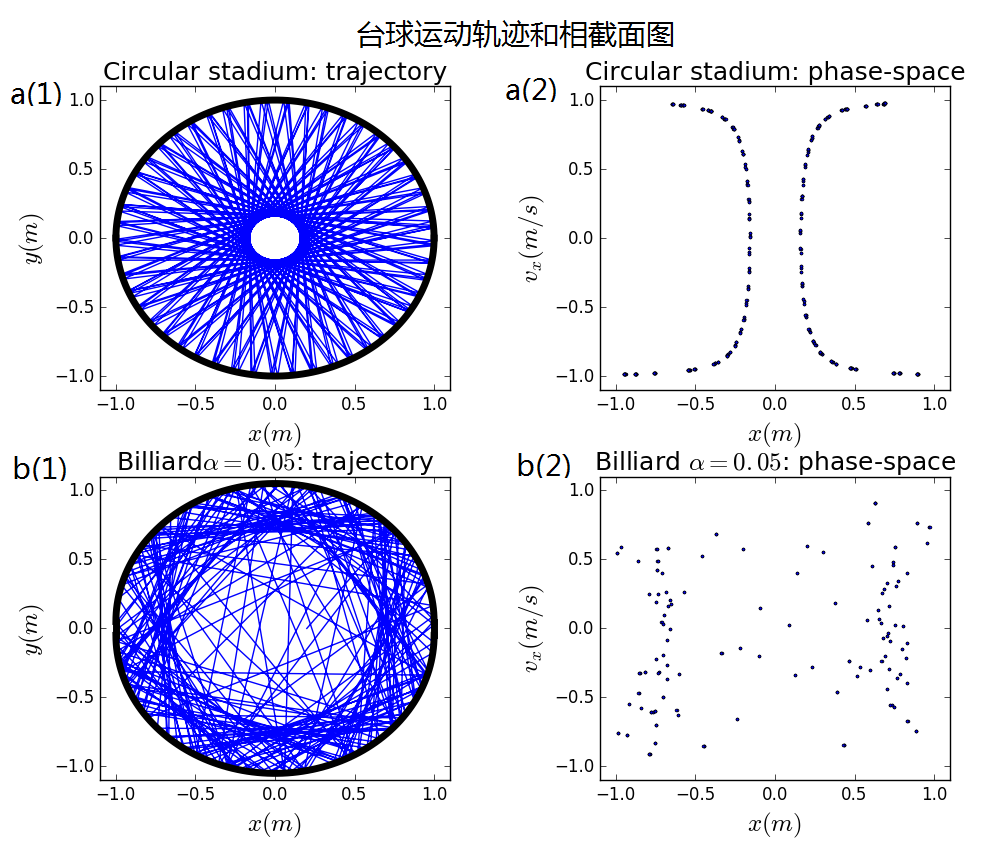
图4 台球运动和相空间截面图图中展示不同边界时的台球运动，图(a1)(a2)分别是边界为圆形时的台球轨迹和相空间$x,v_x$在$y=0$的截面。图(b1)(b2)则分别是边界为体育场形状$\sigma=0.05$时的台球轨迹和相空间$x,v_x$在$y=0$的截面

　　另外，直接展示体育场形边界台球的运动动态图像，同样使用MMA作图，程序附在文末。结果如下图5所示

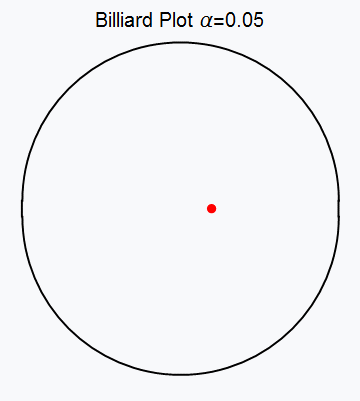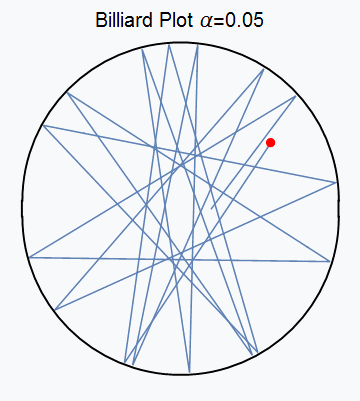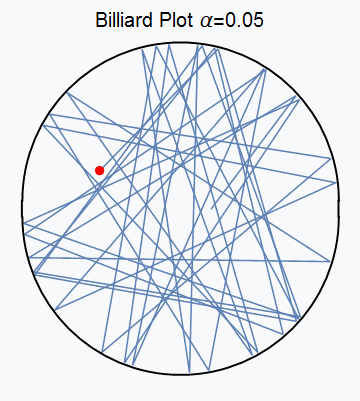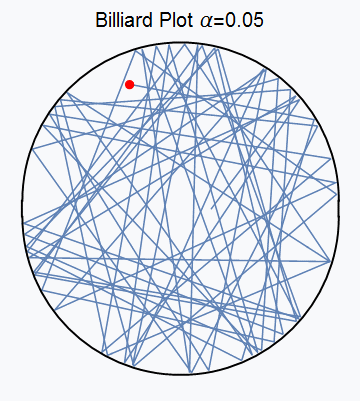
图5 台球运动动态图图展示体育场形边界$\sigma=0.05$时台球的运动情况，台球运动几乎可以铺满整个台面，运动呈现混沌特征。

边界为椭圆时的台球运动

　　当适当改变边界形状时，会有更多的现象发生，一般来讲，边界形状不是圆形等高度规则的形状时，台球运动是混沌的，但是当边界是圆锥曲线时，应该可以期盼台球运动具有一定的规则。下图6展示了边界是椭圆的情况，相应的程序见ch3_Billiard_elliptical.py，并且台球发射位置恰为椭圆焦点，这样台球运动每次都会再次经过焦点。

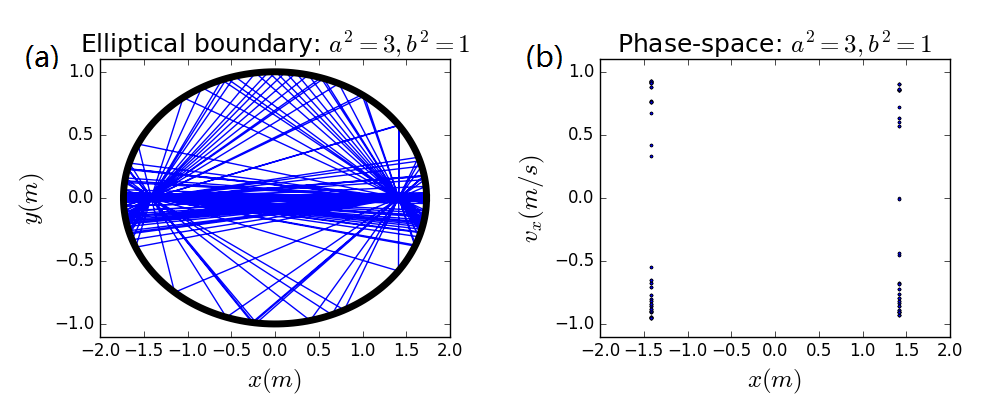
图6 椭圆边界的台球运动边界为椭圆时的台球运动情况，长短轴分别是$a=\sqrt{3},b=1$，台球从焦点出发，将会不断回到焦点。(a)图展示台球轨迹，而(b)展示台球相空间$x,v_x$的图形，取$y=0$的截面，由于台球每次都必须经过焦点，因此截面只会出现在$|x|=\sqrt{2}$。

　　同样，我们展示椭圆边界台球运动的动态图形如下图7所示，因为本人机子用不了vpython，同样只好用MMA作图，程序也附在文末。

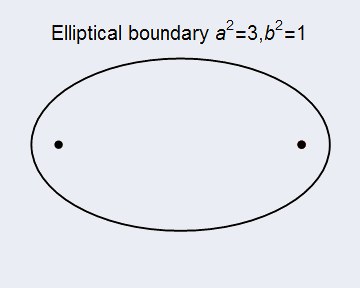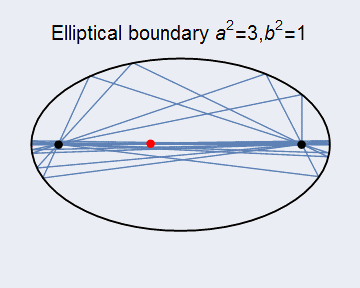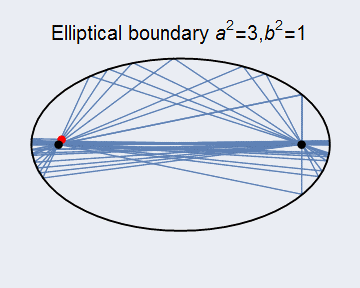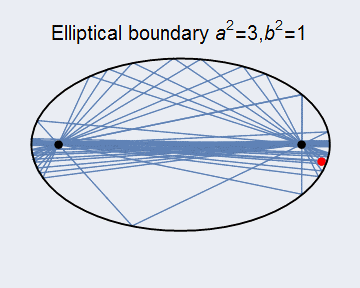
图7 椭圆边界台球动态图边界为椭圆时的台球运动情况，长短轴分别是$a=\sqrt{3},b=1$，台球从焦点出发，将会不断回到焦点。

分子运动浅涉

刚球模型和其相变

　　分子运动是极端复杂的，前面的台球运动已经展示了即便是单个台球在不规则边界下也会出现混沌现象。而分子运动不仅仅要考虑边界，还要考虑各种相互作用，因此给直接求解分子运动带来困难。我们利用前面的台球模型，并进一步假定台球之间的碰撞是弹性的(刚球或硬盘模型)，来数值模拟分子数不多的情况下分子的运动。下图8展示了分子运动的模拟结果，相应的程序见ch3_rigidball.py，图像同样用MMA作出，程序附在文末。

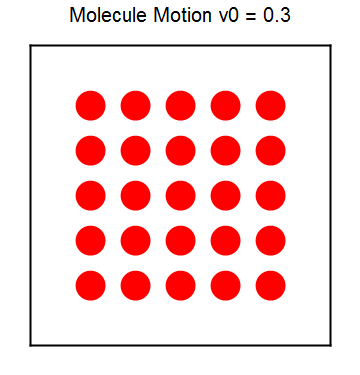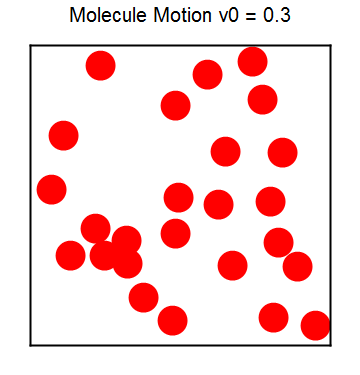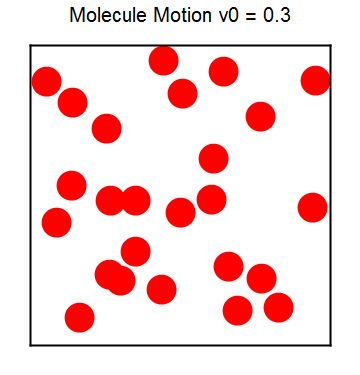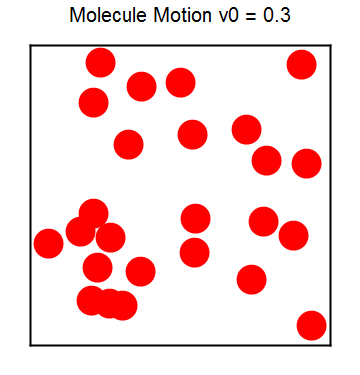
图8 分子刚球(硬盘)模型动态图分子运动刚球模型模拟结果，边界为硬边界，刚球之间的碰撞是完全弹性的，刚球的半径是0.05，初速度是0.03，长度单位都是容器边长。

　　刚球模型虽然简单，但毕竟可以看作是有相互作用的模型。相比于无相互作用的气体模型，刚球模型可以发生相变。为消除边界的影响，我们加上周期性边界条件，另外我们让温度不断降低，观察刚球的聚集情况以展示相变过程，程序同上。

图9 刚球模型的降温相变如图所示，计算步长取为$dt=0.1$，每步降温$0.0001$，即每单位时间降温0.001。刚球半径$r=0.02$，共计有400个刚球，其初始是规则排列的，然后随机给与初速度，初速度大小是服从正态分布的，刚球在降温下发生了相变，有部分刚球聚集起来，因降温过快，另有一部分未能聚集起来

小结

　　本次作业讨论了混沌产生的两个模型——LORENZ模型和桌球模型。可以发现，即便是极端简化的天气模型或是稍微对称破缺的桌球问题，都会明显地带来混沌现象。因此不难理解混沌现象的普遍性。这种普遍性以及混沌现象的内复杂性直接给分子运动的求解带来很大的麻烦。我们建立的简单的刚球(硬盘)模型，在分子数较少的情况下展示了分子运动和降温相变过程。

致谢和引用

[1] 计算物理；Nicholas J. Giordano, Hisao Nakanishi.
[2] 常用数学符号的LaTex表示方法；http://www.mohu.org/info/symbols/symbols.htm.
[3] matplotlib-绘制精美的图表；http://old.sebug.net/paper/books/scipydoc/matplotlib_intro.html.
[4] MMA绘制GIF程序
　　LORENZ模型的相图：mma_plot3d.nb。
　　桌球模型的运动过程：圆形边界mma_billiard3d.nb；
　　　　　　　　　　　　椭圆边界mma_elliptical_3d.nb。
　　分子运动模拟作图:mma_molecule_3d.nb。