计算物理第9次作业　混沌：Chaos

作者：陈洋遥 学号2013301020169 更新时间：20160424

内容目录

本文摘要

　　本次作业研究混沌(Chaos)现象。混沌是自然界普遍存在的现象，特别是1963年，从Lorentz研究气象系统的热对流问题开始，人们逐渐意识到混沌现象的重要性和普遍性。混沌过程的特点是：(1)混沌过程虽是在决定性系统进行的，然而系统的演化确是难以预测的，这主要是因为混沌系统对初值极为敏感。(2)混沌过程的不可预测性并不代表其完全无法研究，我们可以通过作出混沌过程相图的吸引子(attractor)来研究混沌过程，并对这个不可预测的过程给出一些“预测”。(3)另外，混沌过程的吸引子具有分形(fractal)结构，这本身就是混沌现象内禀的普遍规律。(4)周期倍增(periodic-doubling)是产生混沌的重要途径，周期倍增的Feigenbaum常数很好的体现了这种产生途径的普适性。本次作业的内容是：
　　(1)完成课后习题3.16，3.17，观察混沌吸引子的分形结构；
　　(2)展示混沌产生的一个机制-周期倍增现象。

研究背景

　　之前早已讨论过带驱动阻尼摆、非线性摆，其运动均可解析地给出；带驱动的阻尼摆出了刚开始运动时的暂态过程是紊乱的，其长时间的之后的运动情况则是周期性的摆动，与单摆运动特征极为相似。而非线性摆也呈现周期性运动，其轨迹与单摆大同小异，然而当把驱动、阻尼、非线性三个因素加在一起后，摆的运动将会呈现有趣的特点，在系统参数合适时，还表现出混沌现象；下面就来逐步展示这样的运动。当同时考虑三个因素时，摆的运动方程可以写为

$$\begin{equation} \frac{\mathrm{d} ^2\theta}{\mathrm{d} t^2}=-\frac{g}{l} \sin \theta-q \frac{\mathrm{d} \theta}{\mathrm{d}t}+F_D \sin(\Omega_D t) \tag{1} \end{equation}$$
其中l是摆线长度，$g$是重力加速度，$\theta$是摆角，$q$是阻尼系数，$F_D$、$\Omega _D$则分别表征驱动力幅度。这样的方程难以解析求解，因此只能期望借助数值方法给出其解。这里我们采用四阶Runge-Kutta方法求解摆的运动。先将摆运动方程写成两个一阶差分方程的形式
$$\begin{equation} \left\{ \begin{aligned} \theta_{i+1} &= \theta_{i}+\omega_{t_m} \Delta t\\ \omega_{i+1} &= \omega_{i}-\frac{g}{l}\theta_{t_m} \Delta t \\ \end{aligned} \right. \tag{2} \end{equation}$$
这里$t_m$是每一步的“中值”时刻，它的选取有赖于各种算法的特点。在四阶Runge-Kutta法里面，是取四个“准中值”处物理量的值的加权平均来代替中值处的物理量值，其具体取法可以参见课本(Appendix A)，这里不再赘述。四阶Runge-Kutta方法稳定性极高，在短时间的计算中，由于Euler-Cormer方法、Verlet方法的计算波动较大，因此四阶Runge-Kutta法能给出更精确的结果，其全局误差将控制在$\Delta t^4$量级，下面就来逐步研究摆动。

非混沌摆与混沌摆

摆随时间的演化

　　我们展示三种不同驱动力幅值时的摆动情况，相应的程序见ch3_chaos_theta_t.py。下图1给出了三种情况下的摆动，驱动力幅值分别为$F_D=0$，$F_D=0.5$，$F_D=1.2$，由左图(a)可以看到，在无驱动的情况下，摆动迅速衰减，弱驱动的情况下，摆动由最初的暂态过渡到稳定的周期性摆动，而驱动力更强一些时，则可以观察到杂乱的混沌摆动。为进一步研究混沌的特征，考虑两个初值相差极小的近乎全同的摆，研究他们的的摆角差异，可以发现在非混沌情况(无驱动和弱驱动)下，两个摆的摆角差异逐渐减小，而在混沌情况，两个摆的摆角差距则逐渐增大，最终增大到极限。可见，混沌系统之所以是“决定性”、“不可预测性”的，其原因就在于尽管摆的方程存在唯一解，但解并不稳定，对初值极为敏感，因而这样的解就导致了混沌运动。

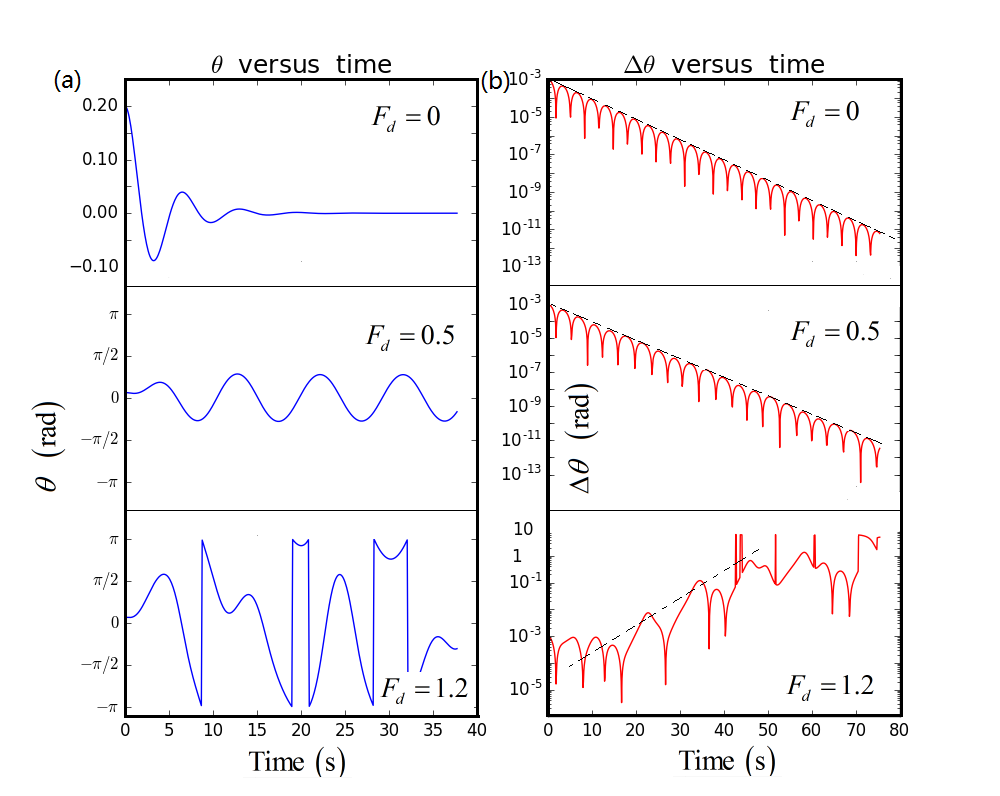
图1 非混沌摆和混沌摆利用四阶Runge-Kutta方法计算的不同驱动力幅值时的摆动情况。左图(a)是单摆的$\theta - t$曲线，在无驱动的情况下，摆动迅速衰减，弱驱动的情况下，摆动由最初的暂态过渡到稳定的周期性摆动，而驱动力更强一些时，则可以观察到杂乱的混沌摆动。右图(b)展示了非混沌情况和混沌情况解对初值的敏感性，选取两个几乎全同的摆，研究它们的$\Delta \theta -t$关系，初始摆角相差$0.001 \mathrm{rad}$，在非混沌情况(无驱动和弱驱动)下，两个摆的摆角差异逐渐减小，而在混沌情况，两个摆的摆角差距则逐渐增大，最终增大到极限。参数取值：$l=g=9.8$，驱动力周期$T_D=3 \pi$，阻尼系数$q=1/2$，计算步长取$\Delta t= 0.01$，单位均为SI单位，摆均从$0.2 \mathrm{rad}$由静止释放。

换一个视角-位形空间的相图

　　混沌摆的运动尽管杂乱无章，但其中具有一般性的规律存在。上面已经展示摆对初值的敏感性，这可以由所谓的Lyapunov指数来刻画，该指数为正数则可断定摆动是混沌的。下面采用相图和Poincare截面来进一步展示混沌运动的其他一般规律。程序可见ch3_chaos_phase.py。左图(a)是弱驱动的摆动，是一个非混沌摆。中图(b)驱动力稍强时的混沌摆。右图(c)是与中图(b)相同的混沌摆，只不过计算时间更长。可以发现，混沌摆的运动即使画在了相空间内，也是极其的复杂，似乎没有任何规律可言。后面将采用所谓Poincare截面的图示法进一步揭示混沌摆的内在特征。

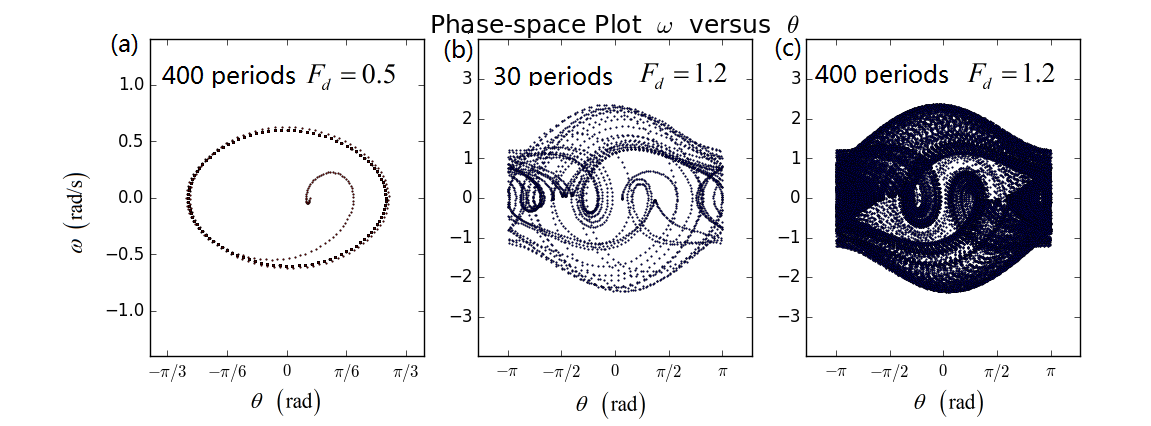
图2 混沌摆和非混沌摆的相图利用四阶Runge-Kutta方法计算的不同驱动力幅值时的摆动的相空间图形。左图(a)是弱驱动的摆动，这是一个非混沌摆，其相图除最初的暂态过程较复杂外，达到平衡后的相几乎是在同一个椭圆周上运行。中图(b)驱动力稍强时的混沌摆，可以看到，摆的相轨线一直杂乱无章，密密麻麻的缠绕在一起，体现了混沌运动的高度非周期性。右图(c)是与中图(b)相同的混沌摆，只不过计算时间更长，可以发现，混沌摆的相轨线除了能量太高的位置达不到以外，几乎要充满整个相平面。参数取值：$l=g=9.8$，驱动力周期$T_D=3 \pi$，阻尼系数$q=1/2$，计算步长取$\Delta t= 0.01$，单位均为SI单位，摆均从$0.2 \mathrm{rad}$由静止释放。

庞加莱截面图-混沌的分形结构

　　上面的相图任然较复杂，为进一步看到混沌运动的内禀特征，我们只取驱动力周期$T_D$的整数倍时刻去观察摆的运动，把这些时刻的相画在相图上，得到所谓的庞加莱截面。用这样的类似于Stroboscope的观察方法，可以大大简化摆动的运动情况。程序可见ch3_chaos_fractal.py。从下图3不难看出，当把截面不断放大时，则可不断发现截面局部存在更精细的结构。

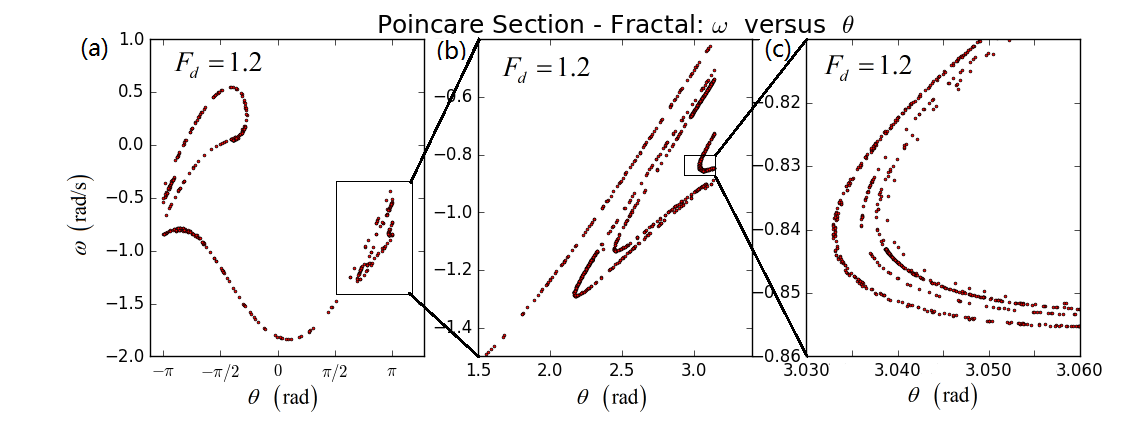
图3 庞加莱截面和分形结构利用四阶Runge-Kutta方法计算的不同驱动力幅值时的摆动的相空间图形，且只取驱动力周期$T_D$的整数倍时刻去观察摆动的相。左图(a)显示的是整个运动的截面，其右边一小块明显有内部结构，放大了察看得到图(b),将图(b)中的一小块放大了察看又得到图(c)，可以想象，如果扫描的时间更长，则可以得到更精细的结构。参数取值：$l=g=9.8$，驱动力周期$T_D=3 \pi$，阻尼系数$q=1/2$，计算步长取$\Delta t= 0.01$，单位均为SI单位，摆均从$0.2 \mathrm{rad}$由静止释放。

混沌产生的机制(之一)-周期加倍

　　从上面的讨论可以看出，当驱动力幅值$F_D$较小时，摆动系统不会产生混沌现象，而若驱动力幅值增加到1.2时，则会产生混沌运动，那么系统是如何从非混沌运动过渡到混沌运动的呢？一般来说，系统从简单运动过渡到混沌运动有不同的机制，然而很多情况下，其混沌的产生均有赖于周期倍增(periodic-doubling)现象，详情可参见课本(Section 3.4)。为讨论周期倍增怎样导致混沌，我们作出所谓的二叉图(bifurcation diagram)，程序可见ch3_chaos_attractor.py。具体做法是，取一系列不同的驱动力幅值，对于每一个幅值$F_D$，计算若干个周期内的运动，也按庞加莱截面的方法，只观察运动稳定后(300个周期以后)驱动力周期$T_D$整数倍时刻的振动角位移$\theta$，并将$F_D - \theta$关系作图如下图4所示。可以发现，驱动力幅值由小于1.0时，系统呈现周期性运动，而在1.0左右之后，则出现分裂现象，但这种分裂不是明显的加倍，最终产生了混沌。这里的非周期加倍致混沌现象并不明确。到了c位置，又出现混沌与非混沌交替的现象。然而在a位置到b位置之间，可以观察到明显的周期加倍现象，最终产生了混沌结果。此后，在e处，混沌与非混沌又交替出现，不过也不是简单的周期加倍。所以说，周期加倍是产生混沌的一种机制，然而可能还有更复杂的方式能产生混沌。

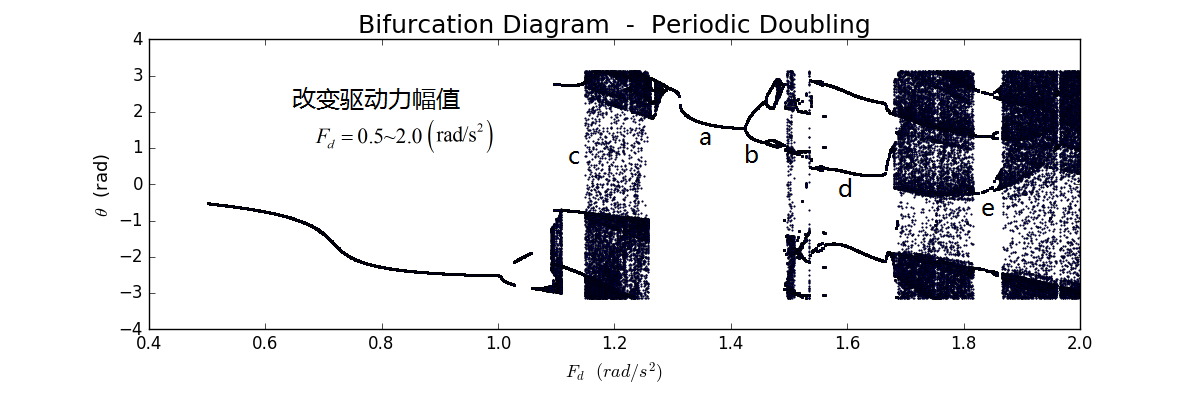
图4 周期倍增二叉图(1)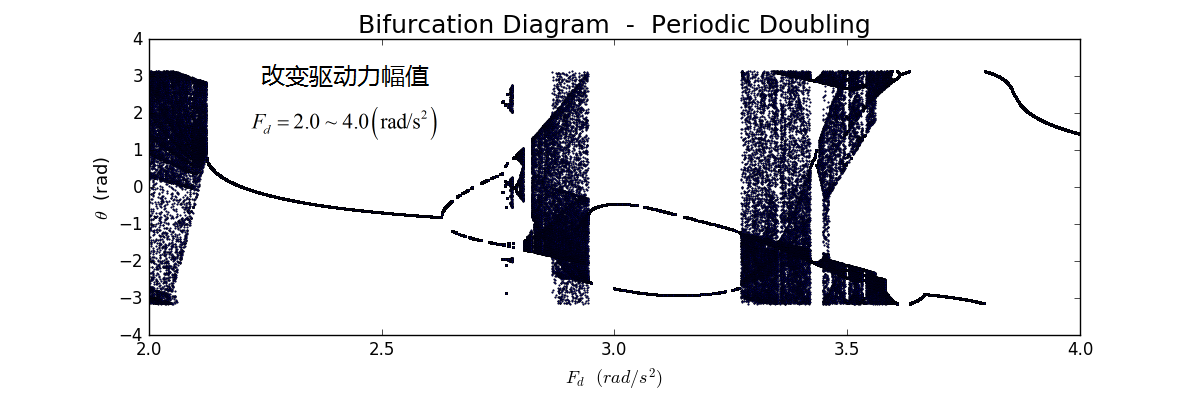 图5 周期倍增二叉图(2)利用四阶Runge-Kutta方法计算的不同驱动力幅值时的二叉图。若系统呈现以驱动力周期$F_D$为周期的周期性运动，则二叉图上应该只呈现一个点(所有点重合)，若出现混沌运动，则此$F_D$对应的二叉图中的点应该形成一条直线。图中a、b过程即是周期加倍位置。参数取值：$l=g=9.8$，驱动力周期$T_D=3 \pi$，阻尼系数$q=1/2$，计算步长取$\Delta t= 0.01$，单位均为SI单位，摆均从$0.2 \mathrm{rad}$由静止释放。

　　二叉图确能在一定程度上反映混沌的产生与否。例如，在上面的图(4)中，挑选d点之后的若干个$F_D$的值，将依次看到摆动系统从简单运动过渡到混沌运动，如下图6所示　　

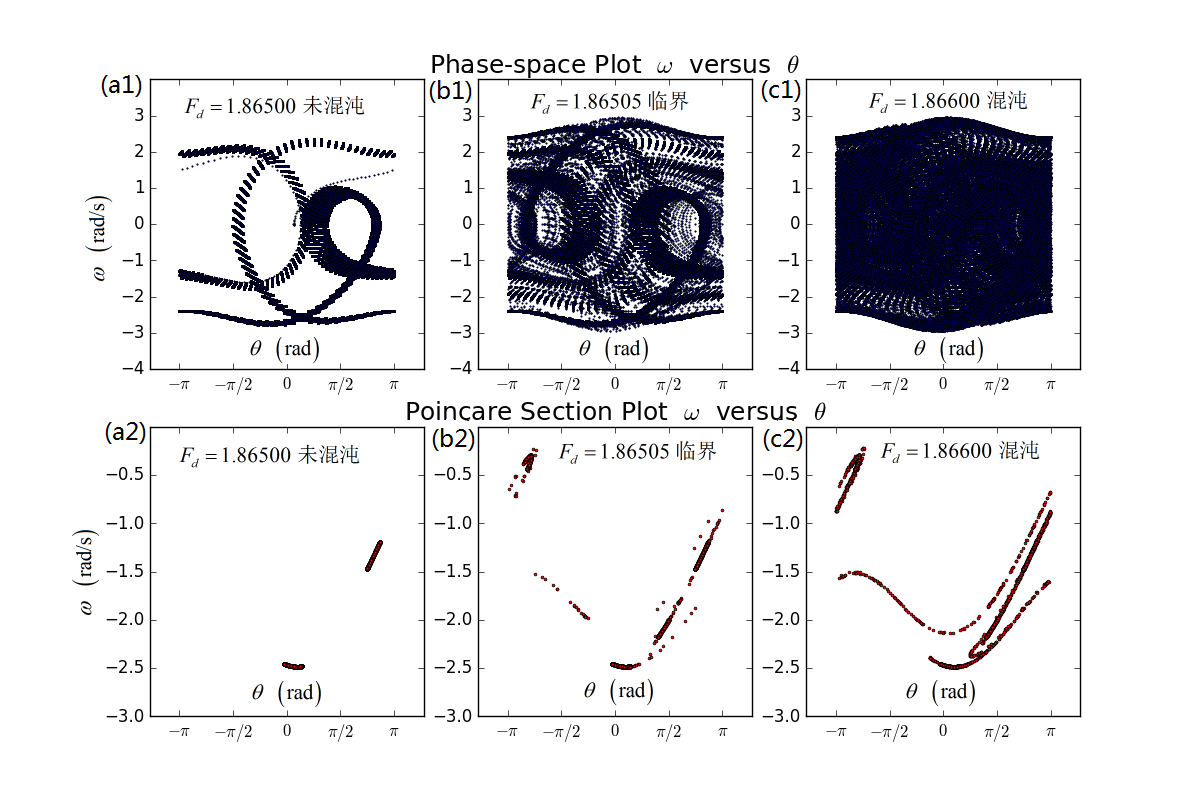
图6 稳定摆到混沌摆的过渡利用四阶Runge-Kutta方法计算的不同驱动力幅值时的摆动的相空间图形。(a)(b)(c)图分别取驱动力幅值$F_D=1.86500,1.86505,1.86600$，可见驱动力幅值发生如此小幅度的变化竟能使摆的状态发生翻天覆地的变化，从一个近乎稳定的态过渡到混沌状态

小结

　　本次作业讨论了混沌现象，通过改变有阻尼、非线性驱动摆的驱动力幅值，使系统由非混沌态过渡到混沌态。作业中利用混沌摆的位置-时间图、相图、庞加莱截面、二叉图等分别展示了混沌摆的运动特征。展示了混沌系统对初值的敏感性，从而确认混沌系统的不可预测性的来源；利用相图和庞加莱截面，则进一步展示了混沌运动的内禀复杂性：其一是相图杂乱无章，几乎充斥于整个一块相平面连续区域，其二是其庞加莱截面存在明显的分型结构；最后，利用二叉图展示了混沌产生的一个机制-周期加倍。

致谢和引用

[1] 计算物理；Nicholas J. Giordano, Hisao Nakanishi.
[2] 常用数学符号的LaTex表示方法；http://www.mohu.org/info/symbols/symbols.htm.
[3] matplotlib-绘制精美的图表；http://old.sebug.net/paper/books/scipydoc/matplotlib_intro.html.