计算物理第8次作业　振动：Oscillatory Motion

作者：陈洋遥 学号2013301020169 更新时间：20160408

内容目录

本文摘要

　　本次作业研究振动问题。振动是自然界最常见的物理现象之一，无论是平静水面上偶然荡起的微微涟漪，还是清风拂过后绿叶的轻轻飘摇，抑或早起目见的第一缕阳光，都是波动现象的真实写照。在所有振动现象中，简谐振动(simple harmonic motion)是最简单的一类，然而，对简谐运动的研究，有利于我们深入了解各种算法的稳定性和局限性；另外，对简谐振子适当增加非线性效应、阻尼、驱动力，则其可能出现混沌(chaos)现象。因此，有必要深入研究简谐运动。本次作业的目的是：
　　(1) 完成课后习题CH3 3.4,3.5;
　　(2) 讨论各种算法(包括Euler，Euler-Cromer，Verlet以及Runge-Kutta法等)的稳定性、计算精度、计算耗时，从而了解各种算法在不同条件下的适用性。

研究背景

　　简谐运动的一个重要的例子就是单摆(simple pendulum)运动，单摆是一小球由不可伸缩的长轻绳紧密悬挂在一固定悬点后，小球所呈现的往复运动形式。在小摆角下，单摆的运动方程即为一振动方程

$$\begin{equation} \frac{\mathrm{d} ^2\theta}{\mathrm{d} t^2}=-\frac{g}{l} \theta \tag{1} \end{equation}$$
其中l是摆线长度，$g$是重力加速度，$\theta$是摆角。若将单摆拉至一角度$\theta _0$后由静止释放，则其运动方程可以解析地给出为
$$\begin{equation} \theta =\theta _0 \cos(\sqrt{\frac{g}{l}} t) \tag{2} \end{equation}$$
此式即说明摆球的运动是正弦形式的，其具有确定的角频率$\Omega=\sqrt{\frac{g}{l}}$，并且振动幅度不随时间发生变化。换而言之，单摆运动的机械能是守恒的。单摆运动虽简单，但其可以作为检验数值方法在一般振动问题中稳定性的试金石，其一是因为可以直接从数值计算的能量是否守恒来判定算法是否足够好，其二则是可以计算很多个周期的摆动以检验算法在运行长时间后的稳定性。
　　一般来讲，很多问题可以用Euler Method进行计算，其基本原理是将微分方程改写为差分方程，并取一阶近似，对单摆问题，也就是
$$\begin{equation} \left\{ \begin{aligned} \theta_{i+1} &= \theta_{i}+\omega_i \Delta t\\ \omega_{i+1} &= \omega_{i}-\frac{g}{l}\theta_i \Delta t \\ \end{aligned} \right. \tag{3} \end{equation}$$
Euler Method的全局误差在$\Delta t$的量级，即随着步长减小几乎线性的减小，因此对于长时间的计算而言，要减小其误差，一般需要很小很小的步长，这对于运算速度是不利的。究其原因，其实是欧拉法每次计算均舍去了二阶项，或者换个说法，总是取每一步的左端点作为“中值”点$t_m$(见教材P457的(A6)式)。因此改进的方法也很简单，取一个更加“中间”的“中值”即可，一个可行的办法由Cromer给出，即所谓的Euler-Cromer Method，其在计算每一步的角频率$\omega_{i+1}$时，仍采用类似于Euler Method的方法，取左端点为中值，然而计算每一步的角位移$\theta_{i+1}$时，就选择右端点作为中值，如此便平衡了中值的不对称性。其计算给出如下
$$\begin{equation} \left\{ \begin{aligned} \theta_{i+1} &= \theta_{i}+\omega_{i+1} \Delta t\\ \omega_{i+1} &= \omega_{i}-\frac{g}{l}\theta_i \Delta t \\ \end{aligned} \right. \tag{4} \end{equation}$$
Euler-Cromer方法尽管只对Euler法作出了一点小小的改动，也不会明显的影响数值计算量，对于更一般的问题，一般也只能将全局误差控制在$\Delta t$量级，但是，对于振动问题(尤其是这里的单摆)，其至少可以将全局误差控制在$\Delta t^2$量级，在超长时间的计算下，其稳定性更为显著，甚至可以超过四阶的Runge-Kutta方法(见下一小节的实例)，因此其是对于振动问题的一个异常有效的算法。另一个类似的方法是Verlet Method，其基本思想是简单的中心差分思想(见教材P465)，其计算式为 $$\begin{equation} \theta_{i+1}=2\theta_i-\theta_{i-1}+\mathrm{d}^2 \theta/\mathrm{d} t^2\times \Delta t^2 \tag{5} \end{equation}$$
与前面方法不同的是，这里不需要计算角位移的一阶导数，因而可以节省一部分计算时间，但是其缺陷是启动计算需要至少两个初值，这就需要我们用其他计算方法先给出第二个初值，再用Verlet Method计算。Verlet Method的全局误差可以在$\Delta t^3$量级，比二阶Runge-Kutta Method还要好，尤其是在振动问题中，其在长时间的稳定性甚至优于四阶Runge-Kutta Method(见下一小节的实例)。
　　其他的计算方法，例如各阶的Runge-Kutta Method，则是通过某些“非中值”的加权平均来给出中值的估计值，其一般计算式为
$$\begin{equation} \left\{ \begin{aligned} \theta_{i+1} &= \theta_{i}+\omega_{t_m} \Delta t\\ \omega_{i+1} &= \omega_{i}-\frac{g}{l}\theta_{t_m} \Delta t \\ \end{aligned} \right. \tag{6} \end{equation}$$
其中二阶的Runge-Kutta Method是取一个中值估计值，而四阶的则是取四个“非中值”的加权平均来对中值进行估计，这里不再赘述，它俩分别能将全局误差控制在$\Delta t^2$和$\Delta t^4$量级，详情可参见课本Appendix A。下面就从欧拉法开始，分析各种方法的稳定性。

单摆运动的不同算法的研究

　　先来看看Euler Method和稍好一点的Euler-Cromer Method对于单摆问题会分别给出怎样的结果，程序见ch3_simple_pendulum_20160415.py。我们展示计算结果如下图由图所示，图1左图(a)给出了用两种方法分别计算单摆和理论值的比较，这里取了步长$\Delta t=0.01s$，远小于摆的周期，可以发现Euler Method的计算相对真实值产生了较大的偏离，而Euler-Cromer计算则好得多。

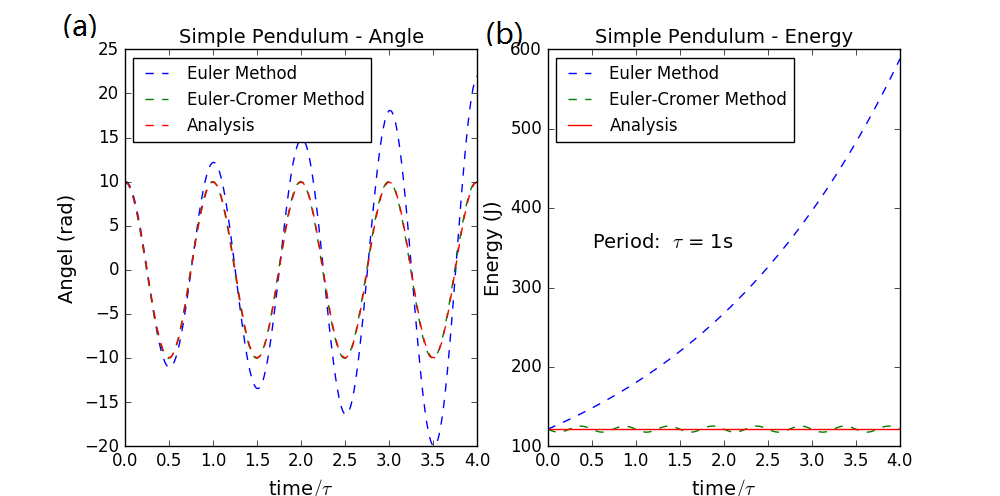
图1 单摆运动的模拟左图(a)利用Euler和Euler-Cromer方法分别计算单摆运动，与理论值对比；右图(b)分别用两种方法给出的单摆能量曲线，Euler Method显著偏离守恒值。参数取值：单摆周期取为$\tau=1$s，计算步长则为$\Delta t=0.01$s，物体质量取为$m=1$kg

不同算法的进一步研究

3周期单摆-欧拉法开始把持不住

　　先考虑一下短时间的单摆，利用Euler、Euler-Cromer、Verlet、二阶Runge-Kutta、四阶Runge-Kutta Method分别计算单摆的能量相对于理论守恒值的偏差，相应的程序见ch3_pendulum_diff_method.py。从图2左图(a)可以发现，即便对于如此短时间的单摆，Euler Method也基本无能为力，其计算出的能量急剧增大，严重偏离事实，而其他的四个方法计算出的能量曲线都还比较平坦，几乎是守恒的。图2右图(b)给出了不同方法的计算精度的比较，可见五种方法计算精度依次上升，但是计算耗时的相应增加。计算精度最高的是四阶Runge-Kutta Method，其精度非常高，而耗时不显著增加，因此还算是比较有效的方法。

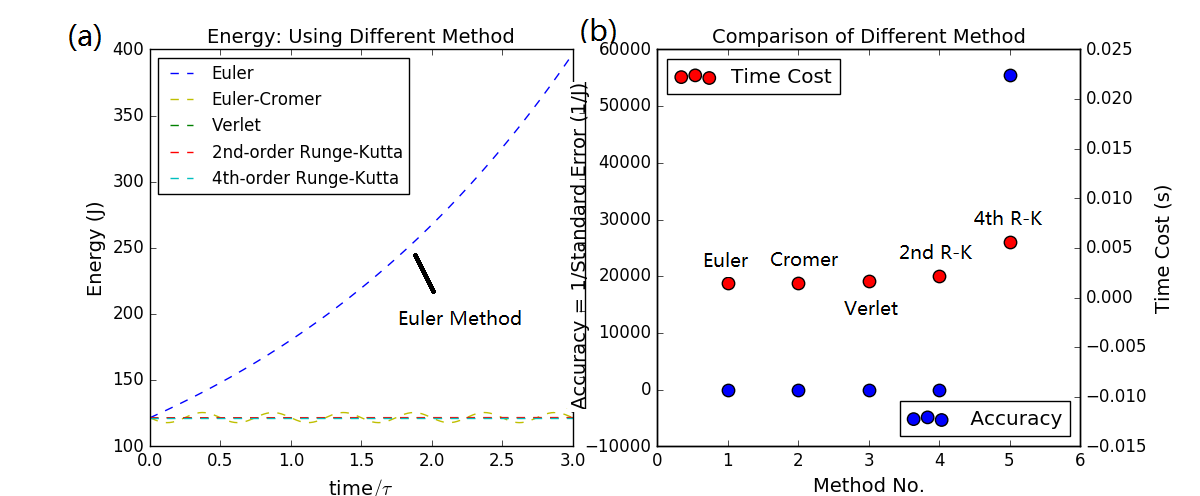
图2 3周期内各种算法的稳定性左图(a)利用各种方法计算出的单摆能量-时间曲线，欧拉法显著偏离真实值；右图(b)分别给出各种方法的计算精度和消耗时间。参数取值：单摆周期取为$\tau=1$s，计算步长则为$\Delta t=0.01$s，物体质量取为$m=1$kg，精度由能量偏差的均方再取倒数给出。

　　我们也给出五种计算方法的精度、消耗时间的具体数据，计算偏差减小时，大致可以发现计算耗时增加，见下表1：

表1 3周期内五种算法的精度、消耗时间

算法	能量偏差(焦耳)	计算耗时(秒)
Euler	$136.2071$	$0.0014$
Euler-Cromer	$2.7027$	$0.0014$
Verlet	$0.0734$	$0.0017$
2nd-order Runge-Kutta	$0.0822$	$0.0022$
4th-order Runge-Kutta	$0.0180 \times 10^{-3}$	$0.0056$

300周期单摆-二阶Runge-Kutta法也开始把持不住

　　再考虑振动时间略长的单摆，考虑到Euler法必然已经严重不稳定，遂利用Euler-Cromer、Verlet、二阶Runge-Kutta、四阶Runge-Kutta Method分别计算单摆的能量相对于理论守恒值的偏差，相应的程序也见ch3_pendulum_diff_method.py。从图3左图(a)可以发现，当计算时间增加到300个周期时，二阶Runge-Kutta法计算的单摆运动的能量曲线已经严重偏离守恒值，因此，此时二阶Runge-Kutta法已经不再稳定，无能为力了。而其他3种方法都还比较不错，能量也大致守恒。图3右图(b)给出了不同方法的计算精度的比较，可见四种方法计算精度各有千秋，但是二阶Runge-Kutta法的精度已经被Euler-Cromer和Verlet方法超越，且其耗时较长。

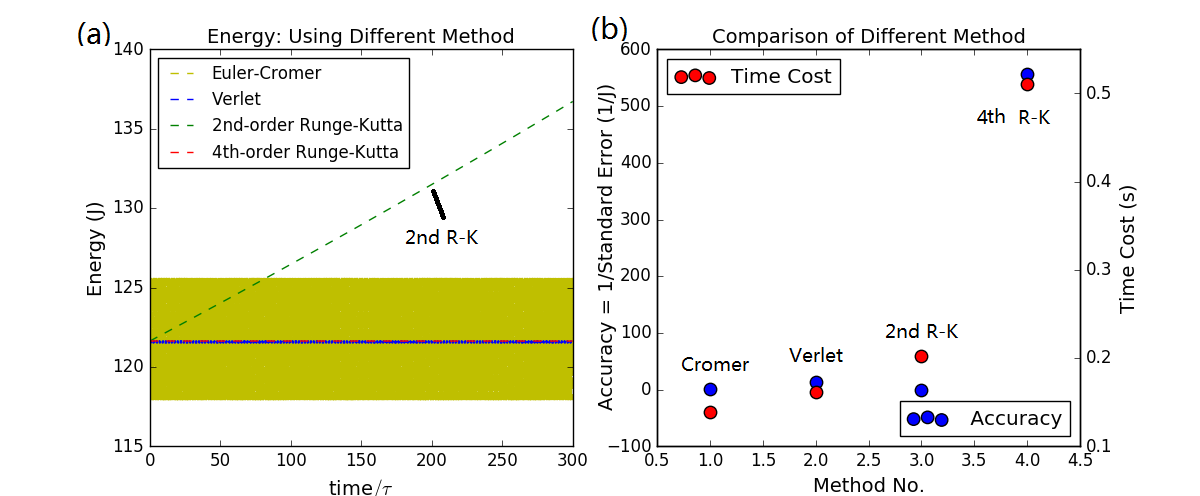
图3 300周期内各种算法的稳定性左图(a)利用4种方法计算出的单摆能量-时间曲线，二阶Runge-Kutta法已经显著偏离真实值；右图(b)分别给出4种方法的计算精度和消耗时间。参数取值：单摆周期取为$\tau=1$s，计算步长则为$\Delta t=0.01$s，物体质量取为$m=1$kg，精度由能量偏差的均方再取倒数给出。

　　我们也给出4种计算方法的精度、消耗时间的具体数据，可以发现，二阶Runge-Kutta法精度已经被另两种方法超越，耗时也长，因而不具有优势，四阶的Runge-Kutta法精度仍然最高，但耗时也最长，且相比3周期情况，Euler-Cromer法的能量偏差增加并不明显，而四阶Runge-Kutta法计算能量偏差显著增大，可以预期，若计算时间继续增加，Runge-Kutta法最终会完蛋。见下表2：

表2 300周期内4种算法的精度、消耗时间

算法	能量偏差(焦耳)	计算耗时(秒)
Euler-Cromer	$2.7072$	$0.1388$
Verlet	$0.0735$	$0.1618$
2nd-order Runge-Kutta	$8.5805$	$0.2028$
4th-order Runge-Kutta	$0.0018$	$0.5107$

20000周期单摆-四阶Runge-Kutta法也把持不住

　　再考虑振动时间更长的单摆，考虑到二阶Runge-Kutta法必然已经严重不稳定，遂利用Euler-Cromer、Verlet、四阶Runge-Kutta Method分别计算单摆的能量相对于理论守恒值的偏差，相应的程序也见ch3_pendulum_diff_method.py。从图4左图(a)可以发现，当计算时间增加到20000个周期时，四阶Runge-Kutta法计算的单摆运动的能量曲线已经略有偏离守恒值，因此，此时四阶Runge-Kutta法已经不再稳定，而其他2种方法都仍保持不错的计算精度。图4右图(b)给出了不同方法的计算精度的比较，可见3种方法计算精度各有千秋，但是四阶Runge-Kutta法的精度已经被Verlet方法超越，也可预见将会被Euler-Cromer方法超越，且四阶Runge-Kutta法耗时相比于其他方法太长，几乎是他们的3倍，这对于更大型的计算是无法忍受的。

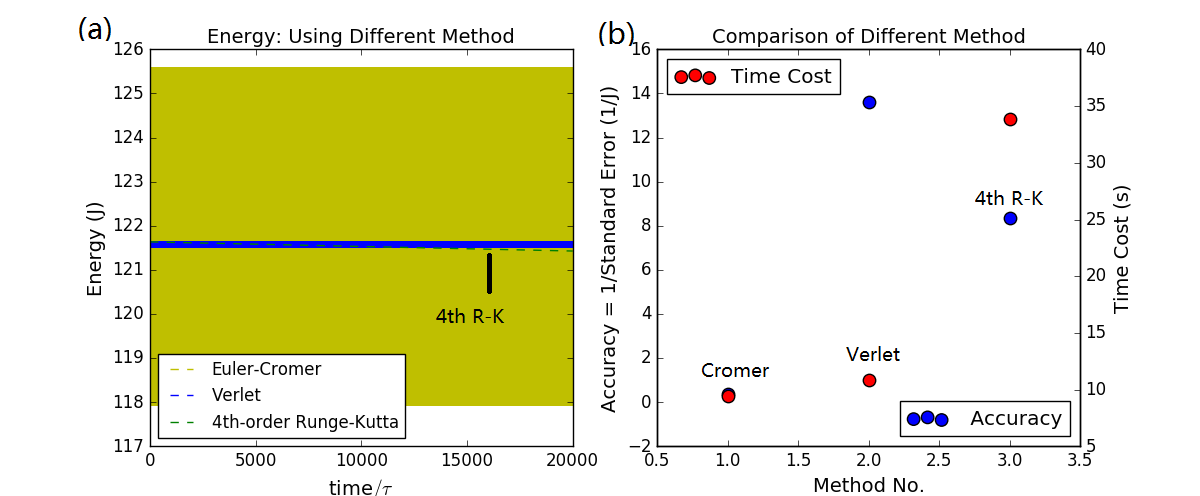
图4 20000周期内各种算法的稳定性左图(a)利用3种方法计算出的单摆能量-时间曲线，四阶Runge-Kutta法已经把持不住了；右图(b)分别给出3种方法的计算精度和消耗时间。参数取值：单摆周期取为$\tau=1$s，计算步长则为$\Delta t=0.01$s，物体质量取为$m=1$kg，精度由能量偏差的均方再取倒数给出。

　　我们也给出3种计算方法的精度、消耗时间的具体数据，可以发现，四阶Runge-Kutta法精度已经被另Verlet法超越，耗时也长，因而不具有优势，且相比300周期情况，Euler-Cromer法和Verlet的能量偏差增加并不明显，而四阶Runge-Kutta法计算能量偏差显著增大，可以预期，若计算时间继续增加，Euler-Cromer法和Verlet法还是能很大程度地保持稳定，且计算时间短，具有很大优势。见下表3：

表3 20000周期内3种算法的精度、消耗时间

算法	能量偏差(焦耳)	计算耗时(秒)
Euler-Cromer	$2.7074$	$9.4055$
Verlet	$0.0735$	$10.8946$
4th-order Runge-Kutta	$0.1198$	$33.9101$

非简谐摆的稳定性-课后习题3.4和3.5

非简谐摆的讨论

　　下面简单讨论以下非简谐摆，与简谐摆不同的是，其恢复力幂次一般不是1次的。一般来说，非简谐摆的运动方程由下式给出

$$\begin{equation} \frac{\mathrm{d}^2 \theta}{\mathrm{d}t^2}=-k \theta ^{\alpha} \tag{7} \end{equation}$$
其中$\theta$为摆角，而$\alpha$为恢复力幂次。上式形式上并不复杂，也容易解析的给出其振动周期$\tau$与振动幅度$\theta_0$的关系(见MMA程序ch3_mathnote.nb)，如下所示
$$\begin{equation} \tau =K(\alpha)\sqrt{\frac{2(\alpha+1)}{k}}\theta_0^{\frac{1-\alpha}{2}} \tag{8} \end{equation}$$
其中$K(\alpha)=\frac{\sqrt{\pi}\Gamma(1+\beta)}{\Gamma(1/2+\beta)}+F(1/2,\beta,1+\beta,e^{i \pi / \beta})$，而$\beta=\frac{1}{1+\alpha}$，$F$是超几何级数。为简单起见，下面均取恢复力系数$k=1$，单位也均取国际单位。经过计算可得当$\alpha=1$时，$\tau=2 \pi$与振幅无关，而$\alpha=3$时，约有$\tau=7.4163 \times \theta_0^{-1}$。$\alpha$取其他值时周期与振幅的关系也可以从$(8)$式给出，但是下面将看到，只有$\alpha=1,3$时才易于数值求解，$\alpha$取其他值时解严重不稳定。下面就来数值求解非简谐摆的运动。

恢复力幂次为3的稳定非简谐摆

　　这里采用四阶Runge-Kutta法计算简谐摆和非简谐摆的振动情况，并给出非简谐摆振动频率对于振幅的依赖。程序见ch3_anharmonic_oscillator.py。从图5左图(a)可以看出，非简谐摆的周期很明显和简谐摆不同(相同振幅时)，而图5(b)则显示了简谐摆的周期不依赖于振幅，而非简谐摆的周期是依赖振幅的，且数值计算的结果和理论曲线吻合得很好。另外这里只去了恢复力幂次$\alpha =1,3$的两种情况，后面将看到，只有这两种情况的摆才比较稳定，而$\alpha$取其他值时，摆对于计算误差极其敏感，将很难以计算。

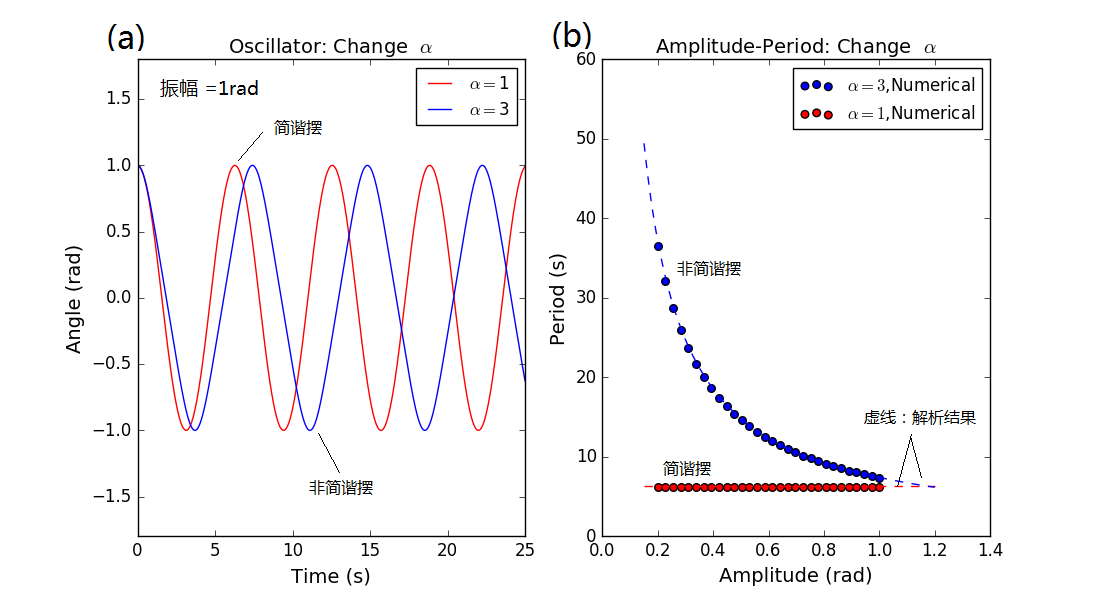
图5 非简谐摆，稳定情况左图(a)给出非简谐摆当$\alpha=1,3$的振动情况，这里默认取力的系数$k=1$，计算步长$\Delta t =0.001s$；右图(b)则给出非简谐摆的振幅色散曲线，即不同振动幅度对应的振动周期(理论和数值解都已给出)。简谐摆的振动周期时与振幅无关的，然而稳定非简谐摆的振动周期是与振幅有关的。

恢复力幂次不是3的不稳定非简谐摆

　　这里仍采用稳定性较好的四阶Runge-Kutta法计算简谐摆和非简谐摆的振动情况。程序见ch3_chaos_nonlinear.py。与之前不同的是，这里取了恢复力幂次$\alpha \neq 3$的情况，可以发现，此时的摆极其的不稳定，其行为严重依赖于计算的误差，采用四阶Runge-Kutta法并将步长取到周期的$1/10000$附近仍然得到发散的结果。此时非线性效应十分显著，用数值计算方法给出的解对计算精度要求十分之高。

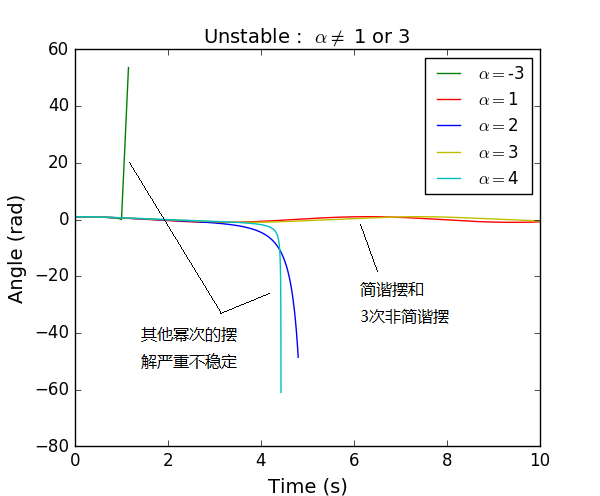
图6 非简谐摆，非稳定情况图中给出非简谐摆的恢复力幂次$\alpha \neq 3$的情况，这里默认取力的系数$k=1$，计算步长$\Delta t =0.001s$，可见这时非简谐摆极其不稳定，对计算误差十分敏感，即使采用稳定性较好的四阶Runge-Kutta方法，步长取到$1/10000$周期附近，数值计算结果也很快严重偏离事实。

小结

　　本次作业讨论了各种算法(包括Euler，Euler-Cromer，Verlet以及Runge-Kutta法等)的稳定性、计算精度、计算耗时，从而了解各种算法在不同条件下的适用性。通过比较可以发现，尽管Runge-Kutta法对于解决大部分问题具有很高的稳定性，但是对于解决振动问题，Euler-Cromer法和Verlet法才是真神，不仅算得快，而且在相当长的时间内能算得很准，这可进一步说明不同系统的最优算法可能不同，应该想办法寻找既简单有高效、精确的方法。
　　另外，本次作业还讨论了非简谐摆的振动问题，可以发现恢复力幂次取值不为1或3时，振动呈现高度的非线性状态，对计算误差十分敏感，对数值求解提出了很大的难题。

致谢和引用

[1] 计算物理；Nicholas J. Giordano, Hisao Nakanishi
[2] 常用数学符号的LaTex表示方法；http://www.mohu.org/info/symbols/symbols.htm
[3] matplotlib-绘制精美的图表；http://old.sebug.net/paper/books/scipydoc/matplotlib_intro.html
[4] 继续参考了刘星辰大神的3d作图方法，这里继续表示$10000^{100}$分感谢，继续顺祝好人一生平安