量子计算1：量子比特

量子计算

---

本文作为文艺青年斌头老师的教师节礼物，记于2017/9/10

0. 前言

本文主要给出量子比特的相关定义，不会对其进行直观解释。本文也会提出部分其他的量子计算知识，比如测量、量子电路等，但这些描述主要为了帮助描述量子比特，所以缺乏一定的严谨性。更多内容可继续参考“量子计算”系列文章。

初入量子计算，最重要的是什么？对概念的熟悉胜于直观的理解。后面有FAQ，有一定的参考价值。

1. 表达

经典计算机中，运算的最小单位是比特。我们称其为经典比特。而在量子计算机中，运算的最小单位也有对应物：量子比特。我们在研究经典计算机的理论的时候，常常把比特作为一种抽象的数学对象，并不考虑实现。当然，学过数字逻辑电路的人一般会了解经典比特如何实现。而在研究量子计算的时候，我们也会把量子比特（有时也称为量子态）看做是一种抽象的数学对象，在研究时暂不考虑实现。当然在实践中，会有其物理对应物进行实现。

经典比特的表达很简单，一个单经典比特只有两种状态:$0$或$1$。而量子比特相对特殊，其有一种通用的表达:Dirac notation:

$$| \cdot \rangle$$
一个单量子比特$| \varphi \rangle$由如下定义：
$$| \psi \rangle = \alpha | 0 \rangle + \beta | 1 \rangle \tag{1}$$
其中:$|\alpha|^2+ |\beta|^2 = 1, \alpha,\beta \in \mathbb{C}$。$| 0 \rangle$和$| 1 \rangle$被称为computational basis state。一个单量子比特是这两个量子比特的一个线性组合，在量子计算中这种线性组合常称为叠加态。

更细化一点，我们常用线性代数来描述量子计算。我们常常把一个单量子比特看做是在$\mathbb{C}^2$（二维复空间）的一个向量.其中$|0 \rangle$,$|1 \rangle$是该空间的两个单位正交基.因此单量子比特就是二维复空间的一个单位向量。一般情况下，我们会令

$$| 0 \rangle = \left( \begin{matrix} 1 \\ 0\end{matrix}\right),| 1 \rangle = \left( \begin{matrix} 0 \\ 1\end{matrix}\right)$$
那么 $$| \psi \rangle = \left( \begin{matrix} \alpha \\ \beta \end{matrix}\right),\parallel |\psi \rangle \parallel^2 = 1$$

上述的$| 0 \rangle$和$|1 \rangle$常常可以对应于经典比特的$0$和$1$，然而由上面的定义可以看出，一个量子比特可以有无穷种状态。

2. 多量子比特

经典计算机下，多比特就是一个0,1比特串。比如说，0000就是一个四比特的经典比特。而量子计算下，多量子比特和经典情况的表达有所类似也有所不同。比如$|0000 \rangle$就是一个四比特的量子比特。乍看之下似乎就是比经典比特多了一个符号，然而其隐藏的数学意义大有不同。请参考 多量子比特与tensor product(未完成)。

一个二位的量子比特表达为：

$$| \psi \rangle = \alpha_{00} | 00 \rangle + \alpha_{01} | 01 \rangle + \alpha_{10} | 10 \rangle + \alpha_{11} | 11 \rangle \tag{2}$$ 在二位量子比特的情况下，computational basis state有四个（以后简称为基本态）。他们要求是标准正交基，张成的空间对应着$\mathbb{C}^4$。二位量子比特就是这四个基本态的叠加态。当然，还要求$\sum_{ij \in \{0,1\}^2} |\alpha_{ij}|^2 =1$。在记号上，常常可以把$| 00 \rangle$写成$| 0 \rangle | 0 \rangle$。

n比特量子态下也有类似定义,它会有$2^n$个基本态,从$|00...0\rangle$(n个0)到$|1...1\rangle$(n个1)，n比特的量子比特就是这$2^n$个基本态的线性组合（叠加态）。一般我们会把基本态所带的线性组合系数（如式(2)中，$|00 \rangle$前的$\alpha_{00}$)称为量级(magnitude)，它会影响测量的结果(后面会简述何为测量)。

一个自然的问题是，量子计算比经典计算好在哪里？从多量子比特的表达上可以初窥一点量子计算的强大：一个n比特的量子态，能够"包含"$2^n$个经典比特的信息(把$|0...0 \rangle$对应为经典比特串"0...0")。比如，简单考虑$n=1$的情况：

$$| \psi \rangle = \frac{1}{\sqrt{2}}(|0 \rangle + |1 \rangle)$$
一个单量子比特，包含了两种信息0,1的"叠加"。然而，如何从这样的“叠加”中提取相应的信息呢？这就需要对量子比特进行测量。

3. 测量

(本部分的描述缺乏一定的严谨性，更多详细内容请参考 测量(未完成)。)

要从一个比特中获得信息。我们需要对其进行测量。而在经典比特中，当我们写一下一个单比特，它的状态就已经定下来：非0即1，这相当于不用测量。（当然在实现中还是要测量：根据电平高低决定0或1）而量子比特有无穷种状态(它是基本态的线性叠加，而其线性叠加系数取值（量级）有无穷多种)，那么对一个量子比特进行测量会得到什么？

回顾到单量子比特:

$$| \psi \rangle = \alpha | 0 \rangle + \beta | 1 \rangle$$

我们说对该量子比特进行测量，并不是测出$\alpha$和$\beta$。而实际上，测量并不能让我们了解该量子比特处于什么状态（因为对$\alpha$和$\beta$的未知）。

很不严谨地讲，对该量子比特进行测量，只会得到两种结果:"0","1"。其中，测得0的概率是$|\alpha|^2$，测得1的概率是$| \beta|^2$。(注意到$|\alpha|^2 + |\beta|^2 = 1$)也就是说，量级对应着其测量结果的概率。

根据"基"的测量

（以下的描述不算很不严谨，算挺不严谨）

一个很自然的问题是，为什么对$| \psi \rangle$测量会得到结果0或1？实际上，此处"0"和"1"只是标明两种状态，两个不同的结果。实际上，当我们进行测量时，还需要指明测量对应的基，上面的描述是基于基$|0 \rangle,|1 \rangle$的测量。比如说，我令:

$$| + \rangle = \frac{|0\rangle + |1 \rangle}{\sqrt{2}}, |- \rangle = \frac{|0\rangle - |1\rangle}{\sqrt{2}}$$

注意，这里的+,-都是记号。容易验证$| + \rangle$、$| - \rangle$是一组标准正交基。我们可以把(1)式重写成:

$$| \psi \rangle = \frac{\alpha + \beta}{\sqrt{2}}| + \rangle + \frac{\alpha - \beta}{\sqrt{2}}| - \rangle$$

如果我们根据基$|+\rangle,|-\rangle$对$| \psi \rangle$进行测量，那么我们会以$|\frac{\alpha+\beta}{\sqrt{2}}|^2$的概率得到结果"+"，以$|\frac{\alpha - \beta}{\sqrt{2}}|^2$得到结果"-"。

注意，在dirac notation里面的0、1、+、-都是记号，表明不同的状态。

例子：薛定谔的猫

薛定谔的猫的故事请自行搜索。看完该故事，我们可以定义一个单比特量子态出来:

$$|猫 \rangle = \frac{1}{\sqrt{2}}| 生\rangle + \frac{1}{\sqrt{2}} |死 \rangle$$

当我们打开盒子，这就相当于对量子态$| 猫 \rangle$进行测量，选取的"基"是$|生\rangle$和$| 死 \rangle$，测量结果以一半的概率是“生”，一半的概率是“死”。

注意，一只猫当然不可能处于既死又活的状态。薛定谔提出该“故事”有其特殊的科学历史背景，详情请自行搜索。

量子崩塌

有一定计算机科学基础和了解大数定律的同学，可能会想：如果我不断地对$|\psi \rangle$测量，比如说，测量10000次，如果得到结果为0的次数为5000，得到结果为1的次数为5000，那么我不就可以认为$\alpha = \beta = \frac{1}{\sqrt{2}}$了吗？也就是说我可以测出一个量子比特究竟处于何种状态。

但实际上，这样是不行的，当我们对一个量子态进行测量，我们得到了相应的输出结果，与此同时我们也破坏了该量子态，使其崩塌，$\alpha、 \beta$的值会被改变。一个量子态测量后会受到什么样的崩塌取决于进行了什么样的测量，具体参考 测量(未完成)。但总之，我们是无法通过测量知道量子究竟处于何种状态。

4. Bloch sphere

表达一个单量子比特的时候，往往可以使用Bloch sphere。在操作单量子比特的时候，使用Bloch sphere也能得到直观上的理解。

由$| \varphi \rangle = \alpha | 0 \rangle + \beta | 1 \rangle$,我们可以重写为:

$$|\psi \rangle = e^{i \gamma}(cos \frac{\theta}{2} | 0 \rangle + e^{i \varphi }sin\frac{\theta}{2} | 1\rangle) \tag{2}$$
($\forall \theta \in R,|e^{i\theta}| = 1,cos^2\theta + sin^2\theta = 1$)

由(2)式，引出Bloch sphere:

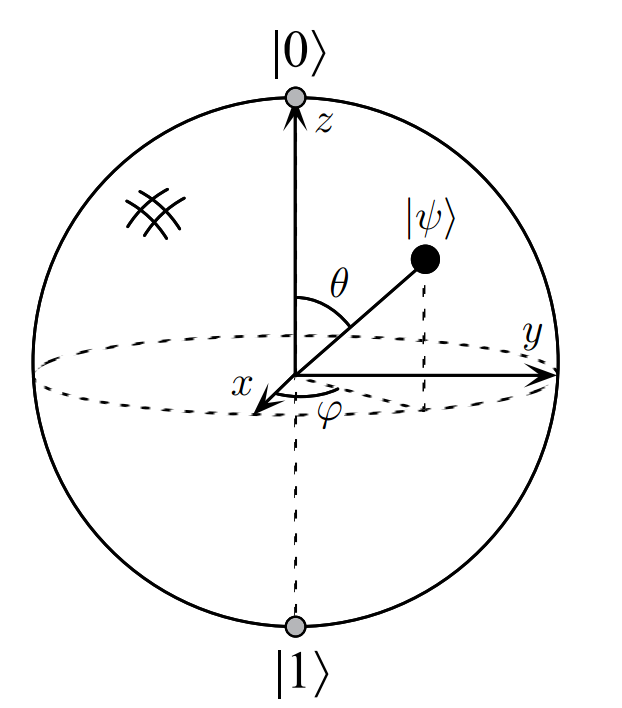
$e^{i \gamma}$并没有在图中体现出来，这是因为$e^{i \gamma}$不具有观测效应，即它的值并不影响结果"0"和结果"1"的测量概率。
$\theta$角意味着量子态在$|0 \rangle$和$|1 \rangle$之间的偏差（实际上应该说为两种不同状态之间的偏差），他决定了两种结果的出现概率。而由于考虑到量级会是虚数，因此要考虑上$e^{i \varphi}$。

可以看出，一个单比特量子态，就对应着这个球面上的某一个点，显然这个球面上有无数个点，即单比特量子态有无穷多个。当我对这个量子态进行测量后，这个量子态就会从原本的地方“跳跃”到球面上的另外一个地方（$\theta、\varphi$被改变)。

一个很自然的问题是：为什么(2)式里要取$\theta/2$？这和这个图有关，当$\theta$为$90^\circ$的时候，量子态应该是在这个球的“赤道”上，它处于$| 0 \rangle$和$| 1 \rangle$的"中间态"，两个基本态对应的量级应该是$\frac{1}{\sqrt{2}}$,而如果不取$\frac{\theta}{2}(cos \frac{\theta}{2} = sin \frac{\theta}{2}=\frac{1}{\sqrt{2}})$而是取$\theta$，那么此时$cos\theta = 0,sin\theta = 1$,

夹角$\varphi$的值并不影响测量得到0或1的概率。如果把x-z平面理解为实数平面的话，那么加上y轴就为整个空间引入了复数。而这个$\varphi$在某种意义上，可以度量量子态$| \psi \rangle$和x-z平面的夹角。当$\varphi$不等于0的时候说明量级是复数。比如说考虑如下量子态：

$$| \psi \rangle = e^{\frac{i \pi}{2}}cos \frac{\pi}{4} | 0 \rangle - sin \frac{\pi}{4} | 1 \rangle$$
由$(e^{i \pi} = -1)$，将上式可重写为: $$| \psi \rangle = e^{\frac{i \pi}{2}}(cos \frac{\pi}{4} | 0 \rangle + e^{\frac{i\pi}{2}} sin \frac{\pi}{4} |1 \rangle)$$
此时$\theta = \frac{\pi}{2}$，$\gamma = \frac{\pi}{2}$，$\varphi = \frac{\pi}{2}$。这个量子态所在的位置应为y轴与球面相交所在位置。

有一点要注意的是，不能因为这个图而得到结论:$| 0 \rangle = -| 1 \rangle$。在考虑这个图的时候，我们应放下之前所说的"$| 0 \rangle$和$| 1 \rangle$是一组$\mathbb{C}^2$的标准正交基"，而是要把视角切换为$| 0 \rangle$、$|1 \rangle$分别是量子态的“两极”，而$\theta$、$\varphi$分别衡量量子态与两极在三维空间下的夹角关系。

5. 量子电路

(未完成)

后语 & FAQ

讲了这么多，迷糊了这么久，究竟什么值得记住？

1. 量子比特的表达:
   
   • dirac notation
   • 单量子比特有无穷多种状态
   • n比特量子态是$2^n$个computational basis state的线性叠加，这种线性叠加称为叠加态
2. 测量:
   
   • 测量结果具有概率性，概率取决于量级，量级不可测。
   • 测量后会崩塌
3. Bloch sphere:
   
   • 一种“直观”的单量子比特表达，球面上的点和单量子比特的状态一一对应
   • $| 0 \rangle$和$|1 \rangle$的夹角是$180^{\circ}$
   • 注意$|\psi \rangle = e^{i \gamma}(cos \frac{\theta}{2} | 0 \rangle + e^{i \varphi }sin\frac{\theta}{2} | 1\rangle)$中的$\frac{\theta}{2}$

FAQ(还在完成中...)

1. 一头雾水怎么办？
   参考上面所说的，记住要记的。提具体的问题。
2. 对“直观”不公平之处在于，直观可帮助概念被理解被熟悉，而不是替代概念。
   或者应该说：直观一时找不到没关系，首重概念熟悉度。