$GF(2^8)$基本运算,求逆,求离散对数实现

密码学 编程 代数

---

前言

GF称为伽罗瓦域，又称有限域.定义详见Galois field.本文讨论GF(2^8)下加减乘除，求逆和离散对数的程序实现。

环境信息

操作系统:ubuntu 14.04
编程语言:C++
编译器:g++

$GF(2^8)$各个运算的实现

以下介绍GF(2^8)各个部分实现细节。

相关定义

由于要多次使用字节类型,因此在本头文件中作一个宏定义

#define u8 unsigned char

由于会设计到简单的多项式除法，因此用一个结构体保存作除后得到的商和余数.

    struct quorem
    {
        u8 first; // quotient
        u8 next;  // remainder
        quorem(u8 i, u8 j){ first = i ; next = j; }
    };

为方便使用，定义一个类以表达GF(2^8)元素

    class GF_eight
    {
        // addition
        inline friend GF_eight operator+(const GF_eight& i, const GF_eight& j);
        // subtraction
        inline friend GF_eight operator-(const GF_eight& i, const GF_eight& j);
        // multiplication
        friend GF_eight operator*(const GF_eight& i, const GF_eight& j);
        // division
        friend GF_eight operator/(const GF_eight& i, const GF_eight& j);
    public:
        // Constructor
        GF_eight(u8 V = 0)
            {
                this->Value = V;
            }
        GF_eight(const GF_eight& V)
            {
                this->Value = V.Value;
            }
        // return value
        u8 getValue() const { return this->Value; }
        // Set the Value
        void setValue(u8 V) { this->Value = V;}
        // Check if it is a generator of GF(2^8)
        bool is_gen() const;
        // Obtain the inverse element
        GF_eight inverse() const;
        //Obtain the g^n
        GF_eight power(u8 n) const;
        //Obtain the dlog based g 
        GF_eight log(const GF_eight& g) const;
    private:
        u8 Value;
    };

其中声明了暂时已实现的$GF(2^8)$元素的操作.private域中的Value是实际保存的值.

加法与减法

$GF(2^8)$中的元素可以看为一个位向量.由于系数是模2的，因此可以把加法看为异或，同样减法也是异或.

    inline GF_eight operator+(const GF_eight& i, const GF_eight& j)
    {
        return GF_eight(i.Value ^ j.Value);
    }
    inline GF_eight operator-(const GF_eight& i, const GF_eight& j)
    {
        return GF_eight(i.Value ^ j.Value);
    }

乘法

稍微麻烦一点的是乘法，实际上执行乘法运算的话只需要按照我们平时的多项式乘法，其中注意模2，乘出来后得到的多项式还要模去$GF(2^8)$的模多项式:

$$m(x) = x^8 + x^4 + x^3 + x+1$$

但这样执行似乎太慢了，我们可以考虑一下更快的乘法.
首先:$m(x) = x^8 + x^4+x^3+x+1$在$GF(2^8)$中代表零元素.因此有

$$x^8 \equiv x^4 + x^3 + x + 1$$
但是这个有什么用呢？我们可以考虑一下如下运算
$$11000000_2 × 101_2$$
根据分配律,我们可以把它写成:
$$11000000_2×(100_2 \oplus 001_2) = (11000000_2 × 100_2) \oplus (11000000_2 × 1_2)$$
很显然，$11000000_2 × 1_2$非常容易算，那么$11000000_2×100_2$呢？还要按先乘后模吗？不需要，我们来看看怎么计算更好.

$11000000_2 × 100_2 = (11000000_2 × 10_2) × 10_2$(这里用了群的结合律)
首先，移位一次:

$$11000000_2 << 1 = 110000000_2$$
既然是$×100_2$，那似乎应该继续移位一次。但我们先不这么做.注意,我们知道了:$x^8 \equiv x^4 + x^3 + x + 1$.它等价于:$100000000_2 \equiv 00011011_2$
因此, $$\begin{align*} 110000000_2 &\equiv 100000000_2 \oplus 10000000_2 \\ &\equiv 10000000_2 \oplus 00011011_2 \\ &\equiv 10011011_2 \end{align*}$$

至此，我们计算出了$11000000_2 × 10_2$,接下来继续计算也是相同的办法.

基于这样的思想，写出$GF(2^8)$的程序

    GF_eight operator*(const GF_eight& i, const GF_eight& j)
    {
        u8 lowest_bit = 0x01;
        u8 highest_bit = 0x80;
        u8 temp_j = j.Value;
        u8 temp_res = i.Value;
        u8 res = 0;
        u8 flag;
        if ( temp_j & lowest_bit )
            res = temp_res;
        temp_j >>= 1;
        while( temp_j != 0 )
        {
            flag = temp_res & highest_bit;
            temp_res <<= 1;
            // Plus 27 if b_8 == 1( flag == 1 )
            if( flag )
                temp_res ^= XXX;
            /* test code
            printf("%x\n",temp_res);
            */
            if(temp_j & lowest_bit)
                res ^= temp_res;
            temp_j >>= 1;
        }
        return GF_eight(res);
    }

注意：程序执行并不严格按照我之前的例子，但思想是一样的。

求逆

在讲如何实现除法之前，首先要考虑求逆.因为我们不能进行普通的多项式除法，因为这是在模下的运算。而求了逆，除法也不过是一个乘法罢了.

由于$GF(2^8)$是一个域，它对乘法运算构成一个交换群。我们可以参考数论里的EGCD算法（扩展欧几里德算法）进行求逆。

EGCD算法由于需要的篇幅不小，因此讲解请参考欧几里德算法与扩展欧几里德算法。注意，这个网站上虽然说的是$Z_p$上的EGCD算法，但是实际上，只要把域元素替换为$GF(2^8)$，把相应的运算进行修改，对相应的变量类型进行一定的修改，得到的新算法就是适用于$GF(2^8)$的EGCD算法.如果你看不懂这句话，那真的需要学点代数了。

求逆的代码在此:

    GF_eight GF_eight::inverse() const
    {
        // Deal with the trivial cases
        if( this->Value == 0)
        {
            printf("Zero element doesn't have inverse!\n");
            return GF_eight(0);
        }
        if( this->Value == 1)
            return GF_eight(1);
        // Using Extended Algorithm
        u8 r1 = 0x8D; 
        u8 r2 = this->Value;
        u8 r3 = 0;
        u8 v1 = 1;
        u8 v2 = 0;
        u8 v3 = 0;
        u8 w1 = 0;
        u8 w2 = 1;
        u8 w3 = 0;
        u8 q = 0;
        quorem p(0,0);
        GF_eight temp(0);
        // Because we use the byte to implement poly_div. So we must
        // deal with the highest bit of the 0x11B before using EGCD.
        // The division is actually the same as the usual division. I just do some operation explicitly( Because we are just allowed to implement in bytes.)
        p = poly_div(r1, r2);
        q = p.first;
        r3 = p.next;
        r3 <<= 1;
        r3 ^= 1;
        q <<= 1;
        p = poly_div(r3, r2);
        q ^= p.first;
        r3 = p.next;
        /* test code
        printf("q:%x\n",q);
        printf("r3:%x\n",r3);
        printf("v:%x\n",v3);
        printf("w:%x\n\n",w3);
        getchar();
        */
        r1 = r2;
        r2 = r3;
        v1 = 0;
        v2 = 1;
        w1 = 1;
        w2 = q;
        // Using EGCD
        while(1)
        {
            //Obtain the quotient and remainder
            p = poly_div(r1, r2);
            q = p.first;
            r3 = p.next;
            if( r3 == 0 ) break;
            // The multiplication must be token in GF(2^8)
            temp = GF_eight(q) * GF_eight(v2);
            v3 = v1 ^ (temp.getValue());
            temp = GF_eight(q) * GF_eight(w2);          
            w3 = w1 ^ (temp.getValue());
            /* test code
            printf("q:%x\n",q);
            printf("r1:%x\n",r1);
            printf("r2:%x\n",r2);
            printf("r3:%x\n",r3);
            printf("v:%x\n",v3);
            printf("w:%x\n\n",w3);
            getchar();
            */
            r1 = r2;
            r2 = r3;
            v1 = v2;
            v2 = v3;
            w1 = w2;
            w2 = w3;
        }
        return GF_eight((u8)w2);

代码很长，我并不擅长写很简洁的代码。。。关于代码的部分解释，我想注释里面已经说了。这里的代码用到了函数poly_div，这个函数的声明为:

static quorem poly_div(u8 ii, u8 jj)

声明为static是因为这个函数只是用于辅助求逆运算的，没必要被用在外面。这个函数完成的是两个字节变量的多项式除法运算 $ii / jj$,并把得到的商和余数保存到结构体quorem中。注意，我们执行的是普通的多项式除法。

除法

完成了求逆之后，就可以直接进行除法运算了:

    GF_eight operator/(const GF_eight& i, const GF_eight& j)
    {
        GF_eight temp = j.inverse();
        return i * temp;
    }

求离散对数

求离散对数的一种很普通的方法就是逐个穷尽进行寻找。但我们实际上可以做得精细一些.可以使用碰撞法

碰撞法的描述可参考:An Introduction to Mathematical Cryptography 的page80, Proposition 2.22:

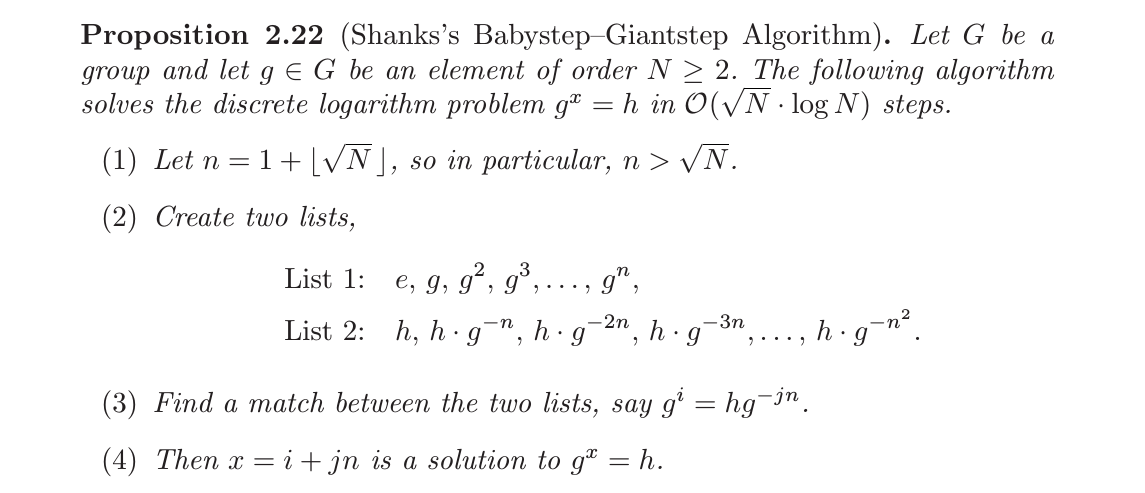
这个算法正确性的证明显然不适合放在这篇文章这里，有想法的人可以自行搜索上面说的电子书进行学习。

同样地，这个原始的算法也是解决$Z_p^*$的离散对数的，但还是那句话，代数告诉我们这个算法可以移植到$GF(2^8)$.

具体实现代码如下:

    GF_eight GF_eight::log(const GF_eight_pack::GF_eight &g) const 
    {
        if( !g.is_gen() )
        {
            printf("The input is not a generator!\n");
            return 0;
        }
        GF_eight temp(1);
        GF_eight h(this->Value);
        // Using the simple algorithm:Collision method to solve g^x = h
        int N = 255;
        int n = sqrt(N)+1;
        // list for finding Collision 
        u8 list[256];
        memset(list, 0, 256);
        // Computing g^0,g^1,...,g^n and record the index i
        u8 i = 0;
        do{
            list[temp.getValue()] = i;
            temp = temp * g;
            i++;
        }while( i <= n );
        temp = temp.inverse(); // temp = g^-(n+1)
        temp = temp * g;       // temp = g^-n
        i = 0;
        u8 j = 0;
        do{
            i = list[h.getValue()];
            if( i != 0)
                break;
            list[h.getValue()] = j;
            h = h * temp;
            j++;
        }while( j  <= n );
        return i + (j*n);
    }

这段代码里面包含了两个辅助函数 is_gen 和 power.它们一个是判断某元素是否是生成元，另一个是快速幂运算。它们的代码请参考后面的完整代码.

完整代码

/*********************************************************************************
 *FileName:     gf.hpp
 *Author:       RunzhiZeng
 *Version:      3.1
 *Date:         16-09-12
 *Description:
                Implementation of add, sub, mul, div, inv and dlog of GF(2^8)
 *Others:
                For Computer Security course
 *History:  
                1. 16-09-12 V3.0:
                        Implement the add, sub, mul and some other miscellaneous functions.
                2. 16-09-13 V3.1:
                        Implement the inv, div and dlog function,also including the power and poly div functions.
 **********************************************************************************/
#ifndef _GF_H_
#define _GF_H_
#include<cstdio>
#include<cmath>
#include<cstring>
namespace GF_eight_pack
{
#define u8 unsigned char
    // x^8
    const u8 XXX = 0x1B;
    // Struct used to save quotient and remainder
    struct quorem
    {
        u8 first; // quotient
        u8 next;  // remainder
        quorem(u8 i, u8 j){ first = i ; next = j; }
    };
    class GF_eight
    {
        // addition
        inline friend GF_eight operator+(const GF_eight& i, const GF_eight& j);
        // subtraction
        inline friend GF_eight operator-(const GF_eight& i, const GF_eight& j);
        // multiplication
        friend GF_eight operator*(const GF_eight& i, const GF_eight& j);
        // division
        friend GF_eight operator/(const GF_eight& i, const GF_eight& j);
    public:
        // Constructor
        GF_eight(u8 V = 0)
            {
                this->Value = V;
            }
        GF_eight(const GF_eight& V)
            {
                this->Value = V.Value;
            }
        // return value
        u8 getValue() const { return this->Value; }
        // Set the Value
        void setValue(u8 V) { this->Value = V;}
        // Check if it is a generator of GF(2^8)
        bool is_gen() const;
        // Obtain the inverse element
        GF_eight inverse() const;
        //Obtain the g^n
        GF_eight power(u8 n) const;
        //Obtain the dlog based g 
        GF_eight log(const GF_eight& g) const;
    private:
        u8 Value;
    };
    inline GF_eight operator+(const GF_eight& i, const GF_eight& j)
    {
        return GF_eight(i.Value ^ j.Value);
    }
    inline GF_eight operator-(const GF_eight& i, const GF_eight& j)
    {
        return GF_eight(i.Value ^ j.Value);
    }
    GF_eight operator*(const GF_eight& i, const GF_eight& j)
    {
        u8 lowest_bit = 0x01;
        u8 highest_bit = 0x80;
        u8 temp_j = j.Value;
        u8 temp_res = i.Value;
        u8 res = 0;
        u8 flag;
        if ( temp_j & lowest_bit )
            res = temp_res;
        temp_j >>= 1;
        while( temp_j != 0 )
        {
            flag = temp_res & highest_bit;
            temp_res <<= 1;
            // Plus 27 if b_8 == 1( flag == 1 )
            if( flag )
                temp_res ^= XXX;
            /* test code
            printf("%x\n",temp_res);
            */
            if(temp_j & lowest_bit)
                res ^= temp_res;
            temp_j >>= 1;
        }
        return GF_eight(res);
    }
    GF_eight operator/(const GF_eight& i, const GF_eight& j)
    {
        GF_eight temp = j.inverse();
        return i * temp;
    }
////////////* Auxiliary functions for finding inverse*///////////////////   
    // Auxiliary function for poly_div
    // Check if i's degree is equal to j's
    static inline bool equal_degree(u8 i, u8 j)
    {
        return ((i ^ j) < i && (i ^ j) < j);
    }
    // Poly division in GF(2^n). n equals to 8 in this function
    static quorem poly_div(u8 ii, u8 jj)
    {
        u8 shift = 0;
        u8 temp = 1;
        u8 res = 0;
        // Trival Case
        if( jj == 0 )
        {
            printf("Error divisor\n");
            return quorem(0, 0);
        }
        if( ii == 0 )
            return quorem(0, jj);           
        if( jj == 1 )
            return quorem(ii, 0);
        // When ii's degree is larger or equal to jj's degree
        u8 temp_j = jj;
        res = 0;
        while( equal_degree(ii, jj) || ii > jj )
        {
            temp_j = jj;
            // Right shift the divisor until the divisor's degree is equal to the dividend's
            while(!equal_degree(ii, temp_j))
            {
                shift++;
                temp_j <<= 1;
            }
            /* test code
              printf("%x\n",temp_j);
            */
            temp <<= shift;
            ii ^= temp_j;
            res ^= temp;
            shift = 0;
            temp = 1;
        }
        return quorem(res, ii);
    }
/////////////////////////////////////////////////////////////////////////
    // Finding inverse using EGCD
    GF_eight GF_eight::inverse() const
    {
        // Deal with the trivial cases
        if( this->Value == 0)
        {
            printf("Zero element doesn't have inverse!\n");
            return GF_eight(0);
        }
        if( this->Value == 1)
            return GF_eight(1);
        // Using Extended Algorithm
        u8 r1 = 0x8D; 
        u8 r2 = this->Value;
        u8 r3 = 0;
        u8 v1 = 1;
        u8 v2 = 0;
        u8 v3 = 0;
        u8 w1 = 0;
        u8 w2 = 1;
        u8 w3 = 0;
        u8 q = 0;
        quorem p(0,0);
        GF_eight temp(0);
        // Because we use the byte to implement poly_div. So we must
        // deal with the highest bit of the 0x11B before using EGCD.
        // The division is actually the same as the usual division. I just do some operation explicitly( Because we are just allowed to implement in bytes.)
        p = poly_div(r1, r2);
        q = p.first;
        r3 = p.next;
        r3 <<= 1;
        r3 ^= 1;
        q <<= 1;
        p = poly_div(r3, r2);
        q ^= p.first;
        r3 = p.next;
        /* test code
        printf("q:%x\n",q);
        printf("r3:%x\n",r3);
        printf("v:%x\n",v3);
        printf("w:%x\n\n",w3);
        getchar();
        */
        r1 = r2;
        r2 = r3;
        v1 = 0;
        v2 = 1;
        w1 = 1;
        w2 = q;
        // Using EGCD
        while(1)
        {
            //Obtain the quotient and remainder
            p = poly_div(r1, r2);
            q = p.first;
            r3 = p.next;
            if( r3 == 0 ) break;
            // The multiplication must be token in GF(2^8)
            temp = GF_eight(q) * GF_eight(v2);
            v3 = v1 ^ (temp.getValue());
            temp = GF_eight(q) * GF_eight(w2);          
            w3 = w1 ^ (temp.getValue());
            /* test code
            printf("q:%x\n",q);
            printf("r1:%x\n",r1);
            printf("r2:%x\n",r2);
            printf("r3:%x\n",r3);
            printf("v:%x\n",v3);
            printf("w:%x\n\n",w3);
            getchar();
            */
            r1 = r2;
            r2 = r3;
            v1 = v2;
            v2 = v3;
            w1 = w2;
            w2 = w3;
        }
        return GF_eight((u8)w2);
    }
    bool GF_eight::is_gen() const
    {
        GF_eight g(this->Value);
        u8 cnt = 0;
        while( g.Value != 1 )
        {
            g = g * (*this);
            cnt = cnt + 1;
            if ( cnt == 254)
                return true;
        }
        return false;
    }
    GF_eight GF_eight::log(const GF_eight_pack::GF_eight &g) const 
    {
        if( !g.is_gen() )
        {
            printf("The input is not a generator!\n");
            return 0;
        }
        GF_eight temp(1);
        GF_eight h(this->Value);
        // Using the simple algorithm:Collision method to solve g^x = h
        int N = 255;
        int n = sqrt(N)+1;
        // list for finding Collision 
        u8 list[256];
        memset(list, 0, 256);
        // Computing g^0,g^1,...,g^n and record the index i
        u8 i = 0;
        do{
            list[temp.getValue()] = i;
            temp = temp * g;
            i++;
        }while( i <= n );
        temp = temp.inverse(); // temp = g^-(n+1)
        temp = temp * g;       // temp = g^-n
        i = 0;
        u8 j = 0;
        do{
            i = list[h.getValue()];
            if( i != 0)
                break;
            list[h.getValue()] = j;
            h = h * temp;
            j++;
        }while( j  <= n );
        return i + (j*n);
    }
    // Quick power
    GF_eight GF_eight::power(u8 n) const
    {
        GF_eight res(1);
        GF_eight a(this->Value);
        while( n > 0)
        {
            if ( n & 1 )
                res = res * a;
            n >>= 1;
            a = a * a;
        }
        return res;
    }
#undef u8
}
#endif /* _GF_H_ */