麦克斯韦妖

量子计算 趣谈

麦克斯韦妖是麦克斯韦在1871年提出的“妖”，它用以说明一种可能违反热力学第二定律的情况。

简单地讲，这个系统是一个被分成两半的绝热容器，这个容器的中间是由“妖”控制的一扇小“门”。容器中有空气分子，它们作无规则热运动时会向门撞击，“门”可以选择性的将速度较快的分子放入一格，而较慢的分子放入另一格，这样，其中的一格就会比另外一格温度高，可以利用此温差，驱动热机做功。
（以上两段摘于wiki）

下图是这样一个模型的直观图（来自于 《量子计算与量子信息（10周年版）》）

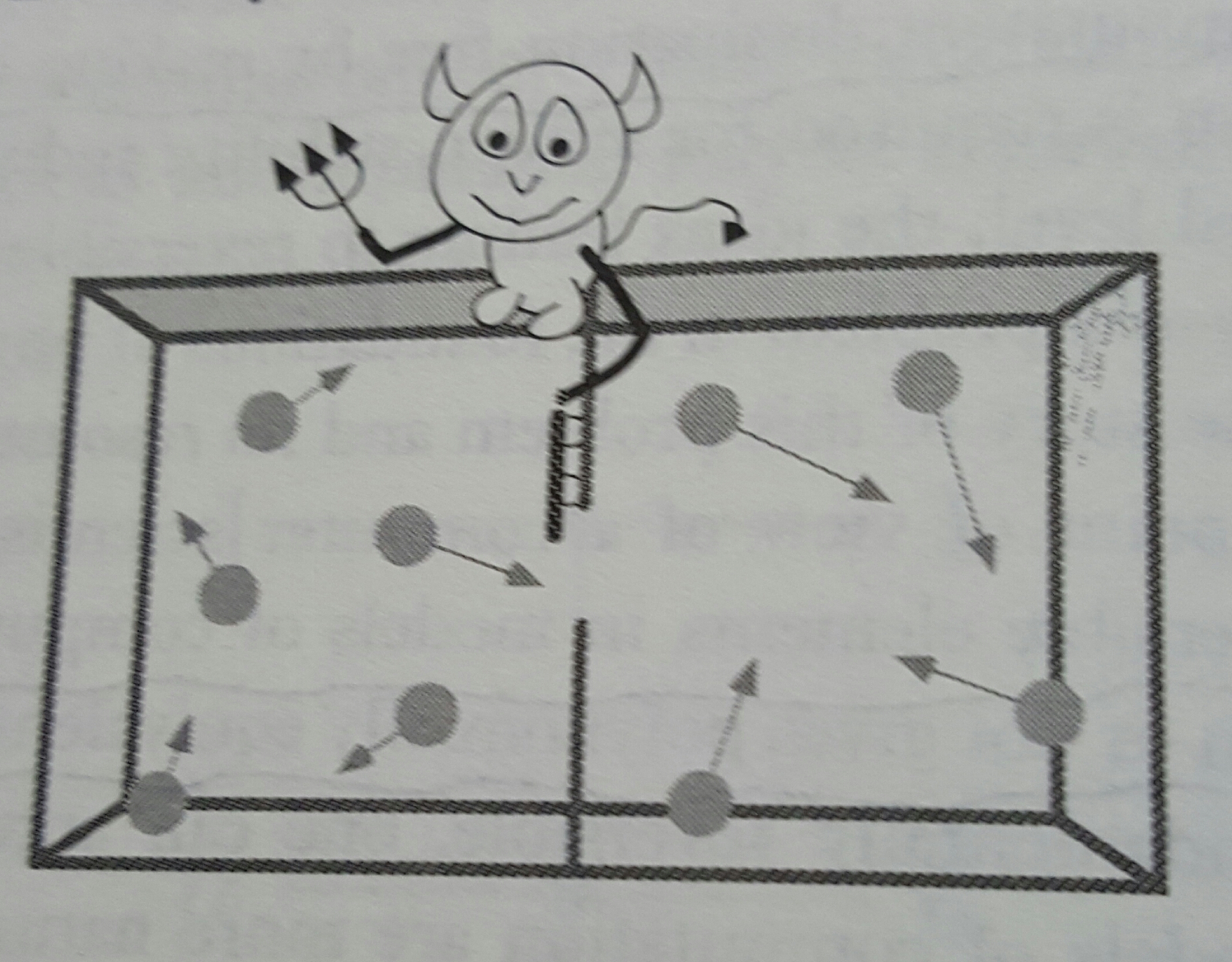
首先看这个模型，第一眼就觉得不合理，但是不合理之处一时又找不到。实际上，科学家解决了这个可能的特例。它实际上并没有违反热力学第二定律，也就是说，这样一个模型仍然是熵增的。

用量子计算的观点来看，首先当有分子撞击这个小门的时候，门要对分子的速率进行测量以确定要不要把分子放过去。进行了测量，那么就需要存放测量结果。也就是说，这个小门要把它对一个分子的速率的测量结果放进它的“内存”里。然而，任何内存都是有限的，总会到某个时间段，这个小门就需要删除某些存储信息以存放新的测量结果。

注意，删除信息是一种熵增行为，这个断言来自于Landauer's principle。

Landauer's principle:Suppose a computer erases a single bit of imformation.The entropy of the environment increases by at least $k_B\log(2)$,where $k_B$ is Boltzmann's constant.

也就是说，当这个小门进行信息的删除时，熵便增加了。而且更精确的分析显示，这个门删除信息的熵增量，不小于这个小妖的行为造成的熵减量（注意，小妖做的事情是熵减的，简单的讲，热冷终平衡是熵增现象，而小妖却让它冷热各一边）。也就是说，最终整个系统的熵都是在增加的，无论你个小妖有怎样的魔力~

麦克斯韦的小妖最终被证实是对第二类永动机的存在性毫无用处，所以我们还是继续好好搬砖吧。

（记于2017-2-12凌晨）