编译原理实验二实验报告

编译原理

1. 实验目标

设计一个应用软件，以实现将正则表达式-->NFA--->DFA-->DFA最小化---词法分析程序
实验要求：
（1）要提供一个源程序编辑界面，让用户输入正则表达式（可保存、打开源程序）
（2）需要提供窗口以便用户可以查看转换得到的NFA（用状态转换表呈现即可）
（3）需要提供窗口以便用户可以查看转换得到的DFA（用状态转换表呈现即可）
（4）需要提供窗口以便用户可以查看转换得到的最小化DFA（用状态转换表呈现即可）
（5）需要提供窗口以便用户可以查看转换得到的词法分析程序（该分析程序需要用C语言描述）
（6）应该书写完善的软件文档

2. 实验环境

操作系统: Windows8.1
编程语言: Java
开发环境: NetBeans8.2

3. 实验步骤

完成部分:(1)~(4)

本实验使用简易的图形界面

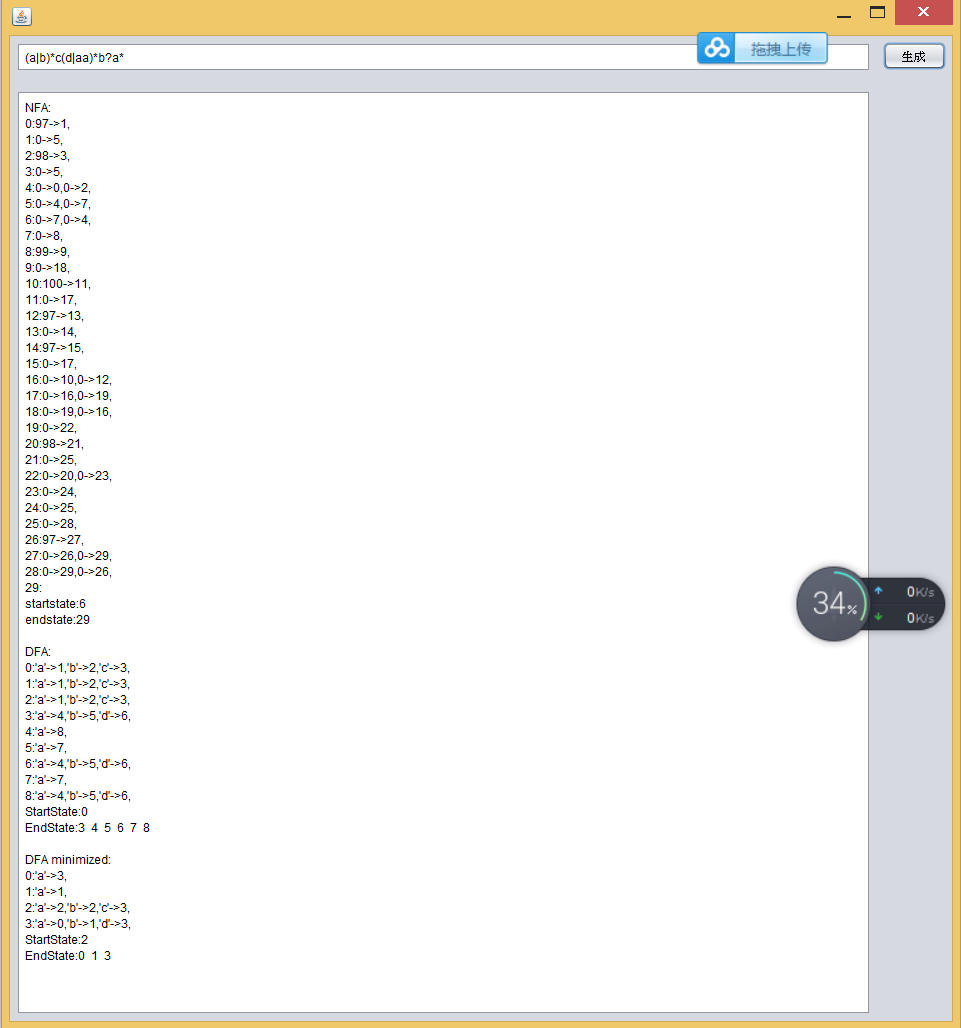
点击生成按钮，将各步骤生成的有限自动机显示出
(由于NFA存在空字符等其它显示不出的字符，因此NFA的显示中，只显示字符的十进制ASCII码。0代表空字符。

NFA类

DEFOFSN类定义了相关的常数
InfixToPostfix定义了相关的中缀表达式转为后缀表达式的函数，但是在本实验该类并没有被使用
NFAGraphEdge,NFAGraphNode分别定义了NFA边和NFA结点
NFAGraph定义了NFA及其相关的函数
test为测试代码

NFA的构造使用了Thompson算法。具体来讲借助了一个符号栈和一个子NFA栈进行构造

算法简易描述如下

1. 首先初始化一张保存NFA的Graph结构
2. 遇到非运算符，及正则表达式里面的转移符号的时候，这里就需要构造一个基本的NFA， 一个初始状态，一个终止状态，然后由初始状态至终止状态有一条为该转移符号的边，此时仍然需要检查正则表达式的下一个符号，如果不是运算符或者为左括号，此时应该运算栈中添加一个连接运算符，然后将构造的基本NFA添加入NFA栈中，方便以后将基本的NFA进行其他选择，重复，连接运算
3. 遇到非运算符时，需要分一下四种运算符的情况
   3.1 如果是运算符“）”，即右括号，此符号属于运算级最高的符号了，所以它要在符号栈中弹出所有符号运算，直到遇到“）”匹配，运算过程中根据符号栈中弹出的符号计算
   3.2 如果是运算符“（”，即左括号，此符号只是用来和右括号结合的，所以直接将该运算符压入符号栈中即可
   3.3 如果是运算符“*”，即重复符号，这个在正则表达式中运算级最高，直接进行计算，计算方法就是从NFA栈中弹出一张图，然后进行构造。构造后检查其后跟随的元素，如果是转移符号或者左括号，则必须要向符号栈中添加连接符号。
   3.4 如果是运算符“|”，由于此符号的优先级没有连接符号高，所以此时应该弹出符号栈中优先级高于它的符号，但是“（”不参与弹出，所以这里只是弹出连接符号和其它"|"符号运算，然后将该符号压入符号栈等候计算。
4. 正则表达式遍历完毕之后，需要弹出所有的符号栈进行计算，最后NFA栈中的唯一NFA就是所求的NFA，然后设置开始状态和接受状态。

DFA类及其最小化

DFANode定义了DFA的结点
DFAGraph定义了相关DFA的结构和函数
partition定义了需要用在DFA最小化里的一些结构。
test为测试代码

DFA的构造大致如下：首先构造NFA，然后根据该NFA进行DFA构造。构造的算法为子集构造法。
算法的具体描述请参考其它资料。直观上讲，NFA的状态转移虽然是非确定性的，但是其转移所到的状态集合必然是其NFA结点集合的幂集的某个子集。因此NFA的非确定性转移可以看作在其幂集子集上的确定性转移，可以把这些子集看作是一个DFA结点。

DFA最小化使用了分割法。把DFA所有的结点分成一个个组，每个组里的DFA结点对任意的输入符号，转移到的状态也是同一组，即组内DFA结点互相不可区分。根据这些组重新构造一个DFA，该新的DFA中各个结点都是不等价的。

本实验完成了以下内容:正则表达式->NFA->DFA->DFA最小化