格的投影

SVP 密码学 格理论

格的投影（或称投影格，翻译问题）是研究格的性质时常用到的概念，尤其是在一些格简约算法(Lattice Reduction algorithm)中。本文介绍格的投影的相关概念。本文假设读者已经对线性代数中投影(projection),正交(orthogonal),正交补集(orthogonal complement),GS(Gram-Schmidt)正交化等概念具有一定的熟悉度。

格的投影和一般的空间的投影有所差异。比如说，把一个3维空间($\mathbb{R}^3$)的所有的点投影到它的一个二维子空间中，显然所有的点仍然还会在原3维空间并且覆盖满整个二维子空间。然而，将一个格点（假设$\mathcal{L} \subset \mathbb{R}^n$）投影到$\mathbb{R}^n$的某个子空间中，这个得到的点会是原来的格中的点吗？进一步的，把$\mathcal{L}$中所有格点投影到$\mathbb{R}^n$的某个子空间中，得到的点集本身会是一个格吗？

首先考虑2维整数格$\mathcal{L} = \mathbb{Z}^2$，将$\mathcal{L}$ 投影到$span\{(1,\sqrt{2})\}$的正交补空间$span\{(-\sqrt{2},1)\}$中。这里的$span\{(-\sqrt{2},1)\}$是属于$\mathbb{R}^2$的子空间。显然投影后得到的点集不会是一个格，因为$\sqrt{2}\notin \mathbb{Q}$。

也就是说，将一个格随意投影到某个子空间中，得到结果不一定会是一个格。但是如果对投影的$E$有要求，那么得到的结果会是一个格（未必是子格）。

定义1. Primitive Lattice(初基格?)
设$\mathcal{L} \subset R^n$为一个$d$维的格，$\mathcal{M} \subset L$是一个$k(k<d)$的子格。
M 是 primitive 的,如果存在一个子空间$E \subseteq R$使得$M = L \cap E$。

prmitive子格的另外一个等价的不严谨的描述是$\mathcal{M}$可以通过扩张（增加基向量）扩张回$\mathcal{L}$。可以由此引出下面的定义

定义2.
设$\mathcal{L} \subset R^n$为一个$d$维的格.一组向量$\{b_1,...,b_m\} \subset L$称为primitive的当且仅当$L(b_1,...,b_m)$是$\mathcal{L}$的primitive子格，即$\exists b_{m+1},...,b_d$使得$\{b_1,...,b_d\}$是$\mathcal{L}$的基.

以下引理描述了格投影后还是格的一种情况。

引理1.
令$\mathcal{L} \subset \mathbb{R}^n$为一个秩为d的格，令$\mathcal{M} \subset \mathcal{L}$是一个秩为r且具有primitive属性的子格$(1 \le r \le d)$。

定义投影操作：$\pi_\mathcal{M}$,它将$\mathcal{L}$中的点投影到 $\mathcal{M}$所在的最小的子空间$(\subseteq \mathbb{R}^n)$的正交补空间（即定义1中的$E$）中。
(该定义可能有些绕，考虑$\mathcal{L} \subset \mathbb{R}^3$是一个秩为3的格，$\mathcal{M}$是一个秩为2的primitive子格,那么$\mathcal{M}$必然包含在某个2维子空间中（而且是最小的，由$\mathcal{M}$的秩为2），那么$\pi_\mathcal{M}$将$\mathcal{L}$中的点投影到这个2维子空间的正交补空间中。)

$\pi_\mathcal{M}(\mathcal{L})$是一个秩为$d-r$的格。

上面的引理证明比较简单，因此这里不作赘述（注意要用到primitive性质）。根据该引理，可知将$\mathcal{L}$投影到$E$也将会得到一个格。同时根据以上引理还会有如下的推论：

推论1
令$\{b_1,...,b_d\}$为格$\mathcal{L} \subset \mathbb{R}^2$的格基，设$M_i$ 为由primitive基 $\{b_1,...,b_{i-1}\}$生成的格。定义$\pi_i = \pi_{span\{b_1,...,b_{i-1}\}}$。则$\pi_i(\mathcal{L})$是一个秩为$d-i+1$的格。

以上推论经常用在格简约算法证明、格难题规约等地方。因为它可以使得我们对格进行归纳。比如说我们要解决秩为n的问题实例时，我们可以把它转化秩为n-1的问题实例进行归纳，将n-1问题实例的解转化为n问题实例的解。

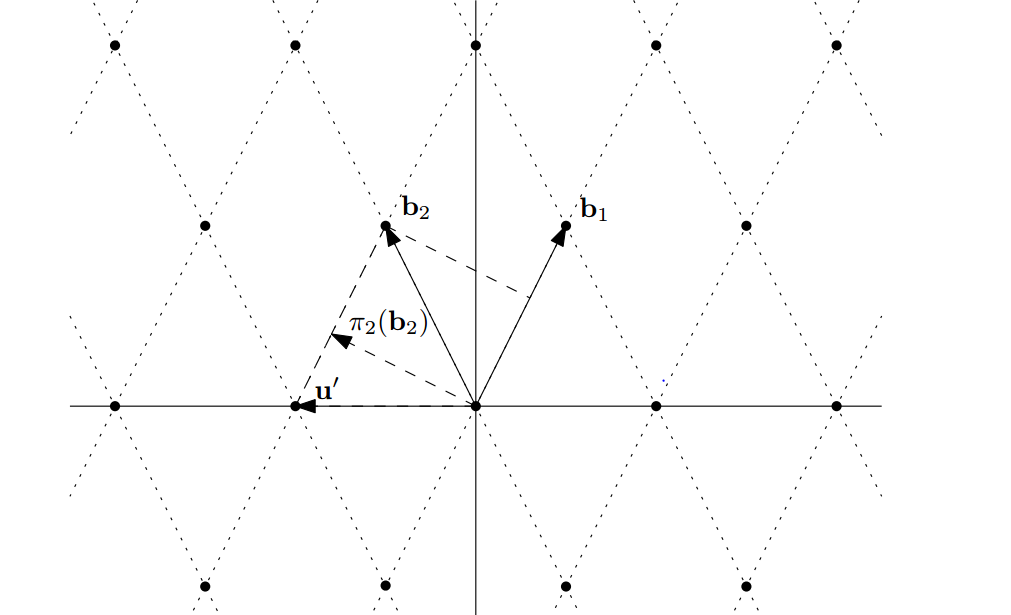
假设现在有一个秩为$d$的格$\mathcal{L}$，我们找到了$\pi_d(\mathcal{L})$里的最短向量$v$，它一般不会在$mathcal{L}$上，那么有没有什么办法，可以把这个$v$ "lift"回$\mathcal{L}$呢(显然不一定会是$\mathcal{L}$的最短向量)。有，下图讲解的就是一个例子

将$b_2$投影到$span\{b_1\}$对应的正交补集上得到$\pi_{2}(b_2)$。由GS变换可知:

$$\pi_2(b_2) = b_2 - \frac{<b_1,b_2>}{||b_1||^2}b_1$$

而将$\pi_2(b_2)$转回原来的格中，只要：

$$u' = b_2 - \lfloor \frac{<b_1,b_2>}{||b_1||^2} \rceil b_1$$

显然$u'$是一个格点。

(高维度的下次更新吧)