自适应线性神经元（Adaptive Linear Neurons）-

神经网络&深度学习

@ author ： duanxxnj@163.com
@ time : 2016-11-14

---

在之前的文章感知机中提到过，感知机分类器是一个非常好的二分类分类器。

但是感知机分类器仍然存在两个比较明显的缺陷：

1. 感知机模型只能针对线性可分的数据集，对于非线性可分的数据集，无能为力
2. 当两个类可由线性超平面分离时，感知器学习规则收敛，但当类无法由线性分类器完美分离

为了解决感知机的这两个主要的缺陷，就有了现在要讲的自适应线性神经元

在之前的感知机中，感知机的激活函数是阶跃函数，这里改为线性激活函数（linear activation function）,一般来说，为了方便，可以直接取：

$$f(a) = a$$

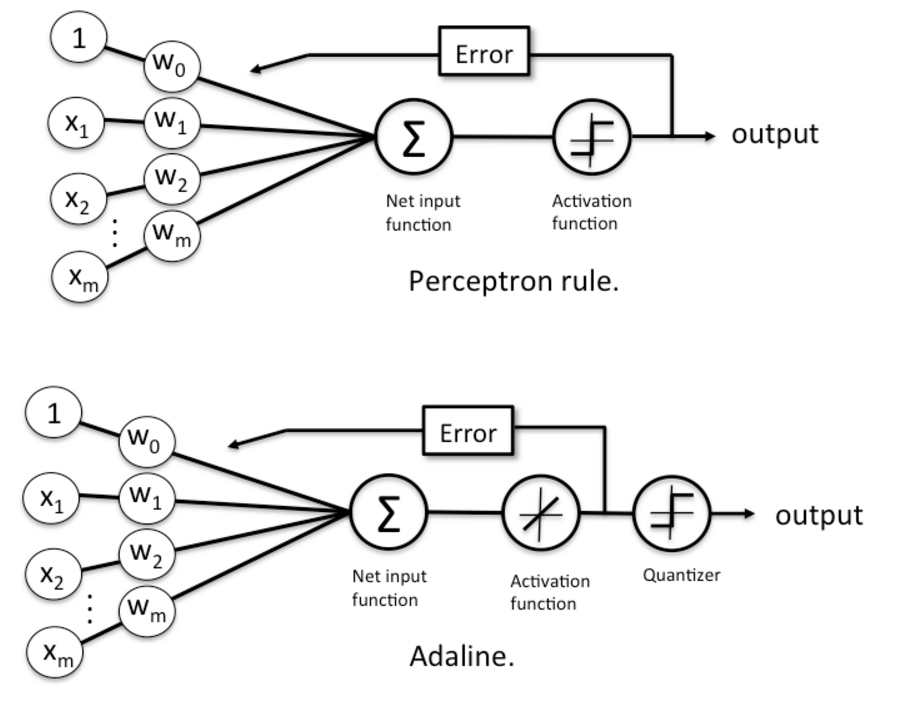
感知机框架和自适应线性神经元框架对比，注意，自适应线性神经元框架比感知机框架多了一个量化器（quantizer），其主要作用是得到样本的类别。

梯度下降法（Gradient Descent）

相对于阶跃函数而言，线性函数有一个明显的优点：函数是可微（differentiable）的。这就使得我们可以直接在这个函数上定义损失函数 $J(w)$（cost function），并对其进行优化。这里定义损失函数 $J(w)$ 为平方损失误差和（SSE： sum of squared errors），这里假设训练样本集合的大小为 $n$：

$$J(w)=\frac{1}{2}\sum_{i=1}^{n}(target^{(i)} - output^{(i)})^2$$

这里的 $1/2$ 仅仅是一个在后面求导时，为了让 $J(w)$ 对 $w$ 求导之后的系数为1，其并不影响最终的结果。

取 $t = target;o = output$，那么 $J(w)$ 对 $w$ 求导的过程为：

$$\begin{aligned} \frac{\partial J(w)}{\partial w} &= \frac{1}{2} \frac{\partial }{\partial w}( \sum_{i=1}^{n}(t^{(i)} - o^{(i)})^2) \\ &= \frac{1}{2} \sum_{i=1}^{n}(\frac{\partial }{\partial w}(t^{(i)} - o^{(i)})^2)\\ &=\frac{1}{2} \sum_{i=1}^{n} ((t^{(i)} - o^{(i)})\frac{\partial }{\partial w}(t^{(i)} - o^{(i)}))\\ &=\frac{1}{2} \sum_{i=1}^{n} ((t^{(i)} - o^{(i)})\frac{\partial }{\partial w}(t^{(i)} - w^Tx))\\ &=-\frac{1}{2} \sum_{i=1}^{n}( (t^{(i)} - o^{(i)})x) \end{aligned}$$

这个推导过程相对非常的简单，其权值更新方式就是：

$$\begin{aligned} w_{t+1} &= w_{t} - \frac{\partial J(w_{t})}{\partial w_{t}}\\ &=w_t + \frac{1}{2} \sum_{i=1}^{n}( (t^{(i)} - o^{(i)})x) \end{aligned}$$

并且，在实际操作中发现，在算法迭代的过程中，需要对数据做归一化，或者叫做标准化处理，这样才能让各个维度的数据的变化范围基本在一个数量级上。最常用的归一化方法是:

$$x = \frac{x - \mu}{\sigma}$$

这里的 $\mu$ 是 $x$ 的均值（mean），$\sigma$ 是 $x$ 的标准差（ standard deviation）。

代码连接

    """
        自适应线性神经元
        这个是感知机的另一种实现方式
        主要区别在于激活函数以及损失函数的选择上
        可以得到一个最优的决策面
    """
    def train(self, X, y, isshow=False):
        n_samples, n_features = X.shape #获得数据样本的大小
        self.w = np.zeros(n_features, dtype=np.float64) #参数W
        self.cost = []
        # standardization of data
        X[:, 1] = (X[:, 1] - X[:, 1].mean()) / X[:, 1].std()
        X[:, 2] = (X[:, 2] - X[:, 2].mean()) / X[:, 2].std()
        if isshow == True:
            plt.ion()
        for t in range(self.n_iter):
            output = self.net_input(X)
            errors = y - output
            self.w += self.eta * X.T.dot(errors)
            self.cost.append((errors**2).sum()/2.0)
            if (t%20 == 0 and isshow):
                print t
                self.plot_process(X)
        return self.cost
    """
        计算网络输入
        X   [n_samples, n_features]二维向量，数据样本集合，其第一列全部为1
        return 网络在激活函数后的结果
    """
    def net_input(self, X):
        X = np.atleast_2d(X)#如果是一维向量，转换为二维向量
        return np.dot(X, self.w)

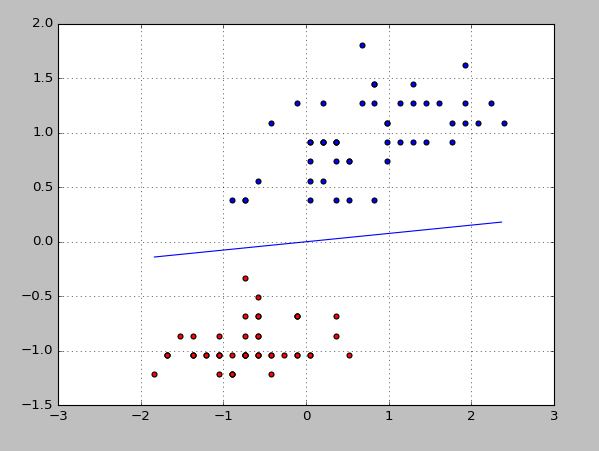
最后可以得到下面这个决策面：

---------------------

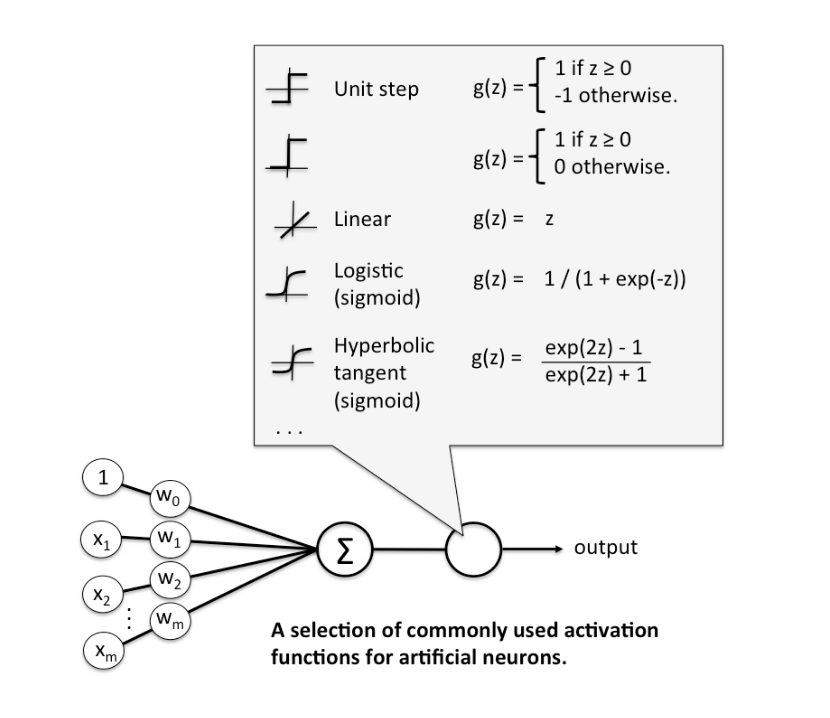
上面已经提到过了，在感知机（也就是神经元）的激活函数上，我们其实可以有很多的选择，不同的激活函数的选择，对应的是不同的分类算法。比如可以对应到Logistics回归，LDA（线性判别分析），SVM（支持向量机）等等，下面给出一些常见的例子，具体的实现及其细节，在后面的文章中会详细的说明。